matlab经济建模之离散模型

离散模型

离散数：可数个 有限数、自然数…… 概率统计：离散型、连续型 模型：差分方程、整数规划、图论、… … 知识：离散数学 集合、代数、图论、逻辑 

 一、层次分析法

 背景

 日常工作、生活中的决策问题：多种方案进行选择

多个旅游点的选择；毕业生工作选择；产品发展方向的选择；选择科研课题……

比较判断时：人的主观选择起相当大的作用

各因素的重要性难以量化

美国数学家T.L.Saaty 于1970年代提出层次分析法  

AHP (Analytic Hierarchy Process)

定性与定量相结合的、系统化、层次化的分析方法

1、模型一：旅游地选择

“五·一”出游：三个旅游点的资料

P1 景色优美；但：旅游热点，住宿条件较差, 费用高

P2 交通方便，住宿条件好，价钱不贵；但景点一般

P3 景点不错，住宿、花费都挺好，但：交通不方便 选择哪一个方案?

 2、基本原理

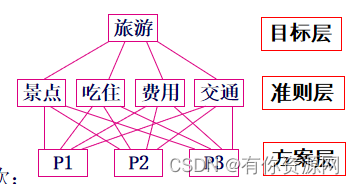
旅游地选择

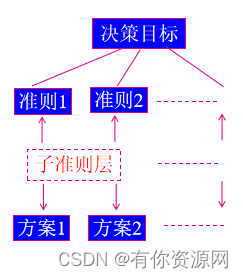
将决策问题分为3个层次：

目标层O，准则层C，方案层P；

每层有若干元素， 各层元素用直线相连

重要性：用权重表示

两两比较

确定各准则对目标的权重——重要性百分比

各方案对每一准则的权重

综合各组权重：确定各方案对目标的权重

基本步骤

（1）确定层次

→ 递节层次结构      

最上层 —— 目标层      

中间层 —— 准则层      

最下层 —— 方案层

例：

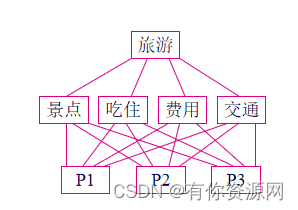
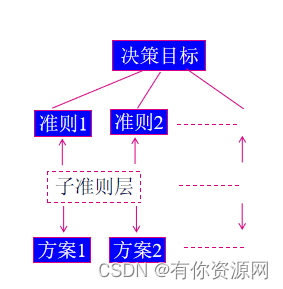
（2）构造两两比较矩阵 

 

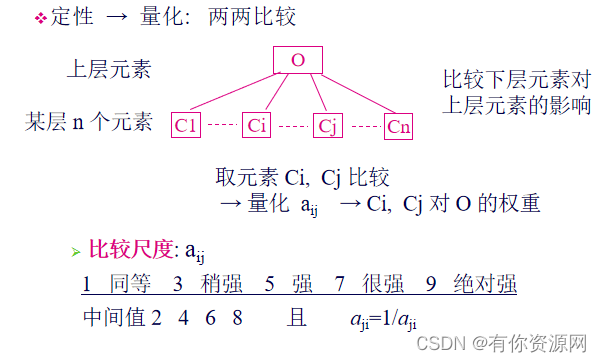
 两两比较矩阵

         A=(aij)n×n 也称为正互反矩阵。

如模型1 建立层次分析模型：

第二层对第一层进行

  C52=10 次比较

例:   P1:P2=3       P2:P4=2

另:   可推得:    P1:P4=6                

               但:    P1:P4=5    

           说明什么?

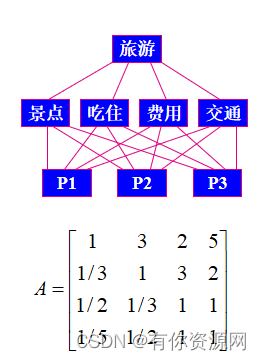
这一点称为比较判断矩阵的不一致性！

理论分析

 （3）计算权重向量

若元素 C1,  C2,……, Cn对 O 的重要性量化比较→权重

令其为     ( w1, w2, ……, wn )

则:   比较矩阵为

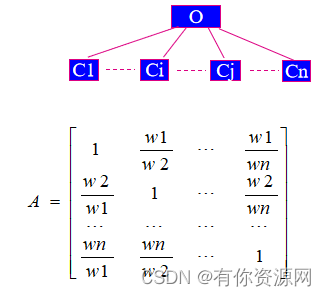
反过来？

由判断矩阵

计算被比较元素对于该准则的相对权重

进行判断矩阵的一致性检验 

 

 计算权向量方法

特征根法

求 A 的最大正特征根 

求 A 的对应于  的特征向量 ( w1, w2, ……, wn )

Matlab命令:

[V,D]=eig（A）    sum

模型一

 

 Matlab得:

λ=4.2137

W=[0.4969    0.2513    0.1386   0.1132]

景色     吃住      费用      交通

另有

近似算法：和法

将 A 的每一列向量归一化      

      

（4）一致性检验

 当 A’ 不一致时, >n

记 A’=A + ,则由 A’W = W 或 AW + W = nW+( -n)W

即: 当( -n)很小时, A’与A 的不一致误差很小

于是有:

一致性指标       CI= ( -n)/(n-1)

随机一致性指标   RI 表

N	3        4        5        6        7        8        9
RI	0.58  0.90  1.12  1.24  1.32  1.41  1.45

一致性比率       CR=CI/RI 

当   CR< 0.1 时, 通过一致性检验

模型一

λ=4.2137

W=[0.4969    0.2513    0.1386    0.1132]T

一致性检验        

 CIA= ( -n)/(n-1) =0.0712；          

RIA = 0.9        

CRA= CI/RI = 0.0791<0.1      

  通过一致性检验

即:  此家庭对        景         吃         费         行  

  的权重为 0.4969    0.2513    0.1386    0.1132

（5）组合权向量及一致性检验

 计算各层元素对于系统目标的总排序权重,并进行排序

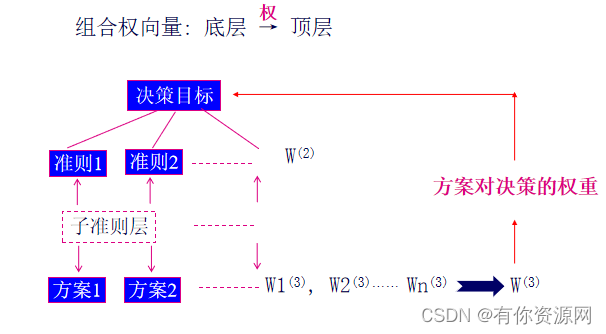
 求组合权向量方法

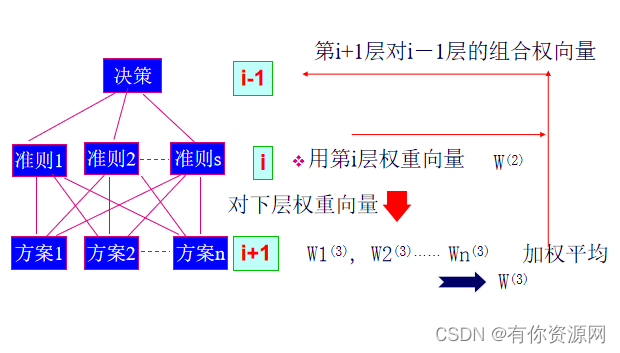
 求组合权向量方法

 

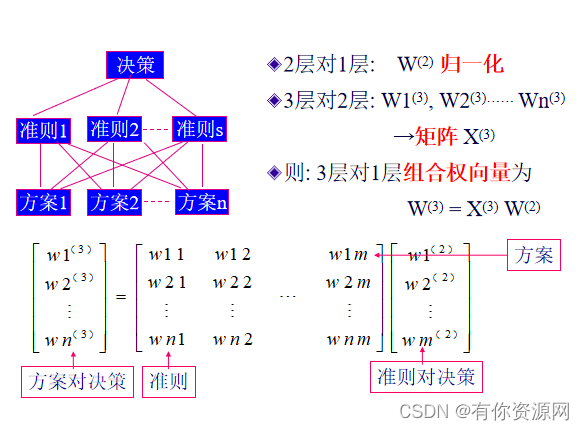
组合一致性检验

 下层一致性指标                                                一致性指标 CI= ( -n)/(n-1)

第i层权重向量：加权平均                                    随机一致性指标   RI 表

第i+1层对i－1层的一致指标CI i+1和RI i+1          一致性比率       CR=CI/RI

组合一致性比率：CR i+1——两层相加

2层对1层: CR(2) = CI(2) /RI(2)  

3层对2层: CI1(3),CI2(3),…,CIn(3);          

          RI1(3),RI2(3),…,RIn(3)

令:  CI (3)= (CI1(3),CI2(3),…,CIn(3)) W(2)      

   RI (3)= (RI1(3),RI2(3),…,RIn(3)) W(2)

一致性比率   CR (3) = CR(2)+(CI (3)/ RI (3))

一致性检验   CR (3) <0.1

模型一 

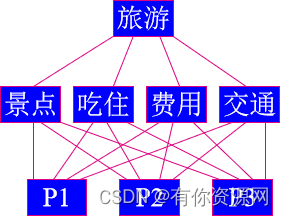
两两比较矩阵

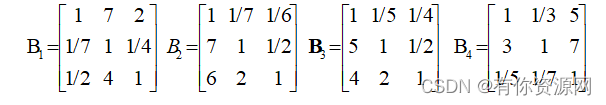
 Matlab计算

特征值特征向量

λ=3.002，W1=[0.6026    0.0823    0.3150]

λ=3.080，W2=[0.0702    0.3707    0.5590]

λ=3.094，W3=[0.0989    0.3643    0.5368]

λ=3.065，W4=[0.2790    0.6491    0.0719]

λ=4.2137, WA=[0.4969    0.2513    0.1386    0.1132]

组合权向量：

W (3) = (W1, W2，W3，W4)

W= W(3) W(2)

W=  [0.3624    0.2580    0.3796]T

一致性检验：

CI1=0.002/2=0.001;          CI2=0.04;     CI3=0.047;   CI4=0.0325    

CR1=0.001/0.58=0.0017; CR2=0.069; CR3=0.081;   CR4=0.056;    

CIA=0.0155/3=0.0712；CRA= 0.0712 /0.9=0.0792

 相对一致性指标均<0.1，通过一致性检验。

组合一致性：

CI (3)= (CI1(3),CI2(3),…,CIn(3)) W(2) =0.0208  

RI (3)= (RI1(3),RI2(3),…,RIn(3)) W(2)=0.0358

一致性比率   CR (3) = CR(2)+(CI (3)/ RI (3))=0.1150>0.1

 未通过一致性检验

另：A=[1 2 3 4;1/2 1 2 2;1/3 1/2 1 1;1/4 1/2 1 1];

答案

组合权向量

W (3) =  [.3617, .2538, .3845]T

A、B、C三个旅游点相对旅游目标来说

综合打分结果是：            

  P3 点为首选，P1 次之，P2 点应予以淘汰。

小结:

建立层次结构

用比例尺度构造对比矩阵      

   A=(aij)n×n

计算权向量(特征向量法),  

   , ( w1, w2, ……, wn )  

并做一致性检验  

CI= ( -n)/(n-1), RI, CR=CI/RI < 0.1

计算组合权向量,  

W(3) =(W1(3), W2(3)…… Wn(3))W(2)    

做组合一致性检验      

CR (3) = CR(2)+(CI (3)/ RI (3))

决策

3、模型二 足球队实力排序

世界杯——6月12日

九八：三十二只劲旅逐鹿法兰西

球赛的胜败： 实力、运气、发挥……

英格兰与阿根廷的相遇让人惋惜

上届冠军巴西与无冕之王荷兰的比赛被称为提前上演的冠亚军决赛

同为战平的比利时和智利命运却不同 ···········

有人认为：偶然性是足球更具魅力

社会学、心理学 → 不讨论

实力水平 → 排序

应用层次分析法

建立层次结构：两层 → 只在一层比较

构造对比矩阵：64场比赛结果

A=(aij)32×32

aij  为球队 Ti 与球队 Tj 的实力标尺

（i、j=1，2……32分别代表巴西、英格兰········）

则： aij0                   aji=1/ aij   （ aij≠0）

          aij=1                   aij=0   （ Ti与Tj成绩残缺）

构造？

 

结果分析

计算结果实力排序：

法国 巴西 挪威 意大利 丹麦 摩洛哥 巴拉圭 尼日利亚 西班牙 克罗地亚 阿根廷 苏格兰 荷兰 智利 南非 保加利亚 沙特 奥地利 喀麦隆 罗马尼亚 比利时 英格兰 牙买加 德国 墨西哥 日本 南斯拉夫 哥伦比亚 韩国 突尼斯 伊朗 美国

国际足联的排序

法国 巴西 克罗地亚 荷兰 阿根廷 意大利 德国 丹麦 英格兰 南斯拉夫 罗马尼亚 尼日利亚 墨西哥 巴拉圭 挪威 智利 西班牙 摩洛哥 比利时 伊朗 哥伦比亚 牙买加 奥地利 南非 喀麦隆 突尼斯 苏格兰 沙特 保加利亚 韩国 日本 美国

挪威：战胜实力强劲的巴西，与意大利战平

伊朗：被认为是表现最好的亚洲队，但      

输给德国、南斯拉夫，以小比分赢美国应对排名影响不大

亚洲队？

关于中国足球。。。。。。

二、公平的席位分配

问题提出：分配代表席位

                   比例加惯例

某校	甲系	乙系	丙系
共200人	100	60	40
20席	10	6	4
调整	103	63	34
人数比例	51.3	31.5	17
20席	10.3	6.3	3.4
实际分配	10	6	4
21席
实际分配

问题:分配不公

原因 20个,丙多占0.6 21个,不充分的席位都在增加

某校	甲系	乙系	丙系
共200人	103	63	34
人数比例	51.3	31.5	17
20席	10.3	6.3	3.4
实际分配	10	6	4
21席	10.815	6.615	3.57
实际分配	11	7	3

欢迎关注有你资源，带你领略matlab的精彩世界~

 

 

最后

以上就是大力芝麻为你收集整理的matlab经济建模之离散模型的全部内容，希望文章能够帮你解决matlab经济建模之离散模型所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。