核心提示:在数字通信中,消息是由一串连续的信号码元传递的。这些码元通常都有相同的持续时间。接收端接收这个码元序列时,一般均需知道每个码元的起止时刻,从而对码元进行判决。例如,用取样判决器对信号进行取样判决时,一般均应对准每个码元最大值的位置。因此,接收端必须要产生一个码元定时脉冲序列,并且定时脉冲的重复频率和...
1.课题背景
在数字通信中,消息是由一串连续的信号码元传递的。这些码元通常都有相同的持续时间。接收端接收这个码元序列时,一般均需知道每个码元的起止时刻,从而对码元进行判决。例如,用取样判决器对信号进行取样判决时,一般均应对准每个码元最大值的位置。因此,接收端必须要产生一个码元定时脉冲序列,并且定时脉冲的重复频率和相位(位置)要与接收码元一致。即:接收端定时脉冲的重复频率和发送端码元速率相同;脉冲位置(即取样判决时刻)对准最佳取样判决位置。我们把在接收端产生与接收码元的重复频率和相位一致的定时脉冲序列的过程称为码元同步或位同步、位定时,而称这个定时脉冲序列为码元同步脉冲或位同步脉冲。
2.课题相关理论概述
Ganrder法是一种不需要先进行载波同步的定时误差估计算法。这种方法是一种非判决指向方法,其基本思想是:提取出相邻码元最佳采样点的幅度和极性变化信息,再加上相邻码元过渡点是否为零这一信息,就可以从采样信号中提取出定时误差。
在系统设计中Gardner锁相环位于Costas载波同步锁相环之后,主要由四部分组成:内插器、时钟误差提取模块、环路滤波器以及控制器模块。Gardner算法的基本结构如下所示:
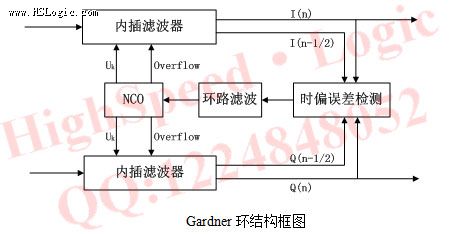
相互正交的I,Q两路信号的采样点通过运算每个符号期间都会产生一个定时错误样点。通过定时误差检测把定时错误序列通过环路滤波器后送给数控振荡器,由数控振荡器产生参数控制插值滤波器,最后插值滤波器进行采样时刻调整,从而完成整个符号同步过程。如何由接收到的采样点产生定时错误序列,这是Gardner算法的关键所在,在后面的章节,我们将详细讨论Gardner环的原理。
环路的基本工作流程这里就不做叙述了,有兴趣的同学可以查看相关的参考文献,内容基本雷同,下面对几个主要模块进行介绍。
时钟误差提取模块
Gardner算法中的每个符号需要两个采样点,一个为符号的最佳观察点,一个为两个最佳观察点之间的采样点。该算法使用与捕获与跟踪两种模式。误差提取模块每个符号周期计算一次,理论计算公式为:
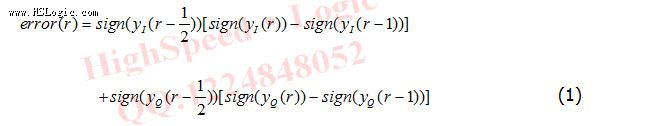
环路滤波器

控制器模块
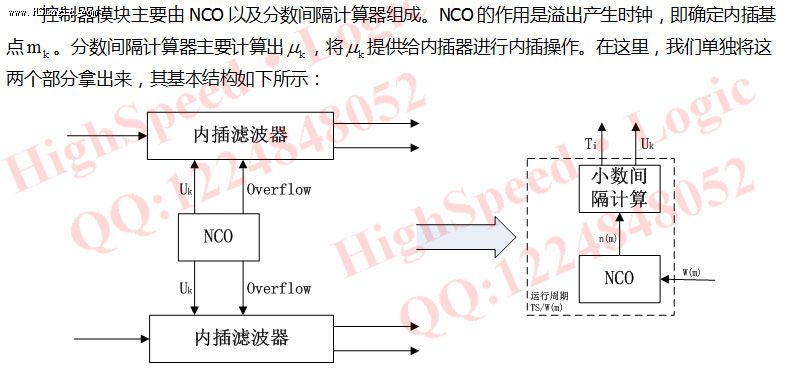
从功能方面看内插估值控制模块的主要完成的任务是计算小数间隔,以及产生再采样时钟Ti。从图中可以看出,内插估值控制模块可以由两部分组成:一是递减计数NCO,二是小数间隔计算模块。NCO采用递减方式进行计数是该设计的精妙之处,采用此设计方案后,只需运用一个简单的相似三角形的方法就能巧妙的计算出小数间隔。
3.相关研究成果
Gardner环的Matlab仿真
前面我们仔细研究了Gardner环的基本工作原理,这里我们将对Gardner环进行仿真,探讨Gardner环的工作性能。在系统仿真前,首先要确定Gardner环的环路系数。在这里,我们取系数C1,C2分别为0.001,0.000001。需要对分数间隔,环路滤波输出,Gardner环输出后的基带信号星座图以及系统误码率进行仿真。
确定了环路滤波器的系数后,就可以开始进行仿真了,根据前面介绍的Gardner环的基本计算流程,我们开始对在不同时偏下进行对系统的仿真。
Gardner环的仿真参数如下所示:
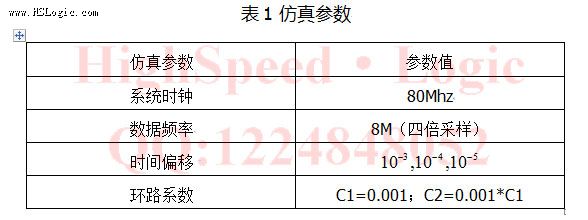
S曲线开环仿真
当位定时提前(定时偏移时刻为负),定时误差信号为负值,当位定时滞后(定时偏移时刻为正),定时误差信号为正值,无定时偏移时(τ=0),定时误差信号位于原点。由于基于GARDNER算法的定时误差信号具有与频率偏移无关的特性。具体仿真如下所示(这里我们设置频偏分别为0k,4k):
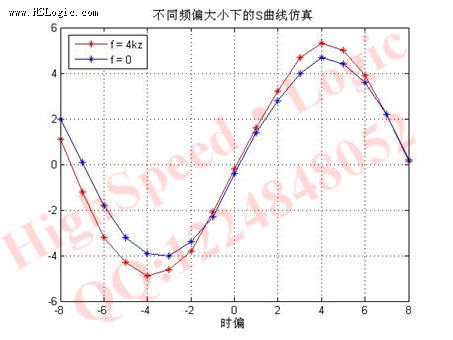
图不同频偏下的S曲线开环仿真图
可见不同的频率偏移条件下,定时误差信号特性曲线除了幅度上有所变化外,它们的基本形状为S形,这表明频差对定时误差信号的影响不大。幅度的不同是由于频偏带来的相位差导致的。所以在一般的中频系统中,这类误差是完全可以忍受的。当然在射频环境下,当系统的相位噪声较大的时候,S曲线可能发送变化,但是其基本形状仍比较接近。这样,我们可以单独的考虑时偏因素对gardner环的影响,并可以在测试环境下使用不带频偏的测试信号进行测试,从而简化了系统的设计复杂度。
Gardner闭环仿真
下面我们对不同时偏的情况进行仿真,以下是时偏为0.0005的情况下,分数间隔和误差信号通过环路滤波后的仿真图。环路输出在0.5上下波动,基本收敛在0.5附近,分数间隔μ,一开始分数间隔μ是不稳定的,但是随着整个定时同步系统的工作,系统达到稳定,此时分数间隔μ逐渐形成收敛三角形,其斜率变小,这是由于时偏变成了0.0005,为原来的1/2。
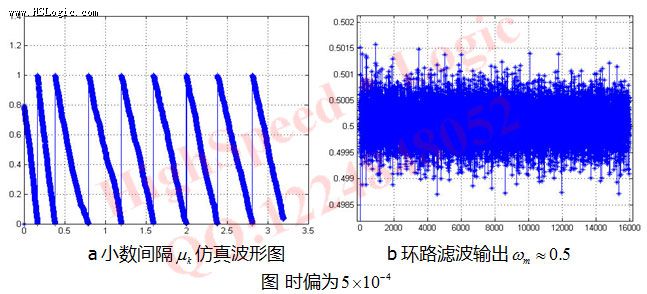
从上面的仿真可以看出gardner环基本能正常工作,其稳定后,误差信号通过环路滤波后其值稳定在0.5左右。其不随时偏变化,而分数间隔μ会变为三角形,三角形的斜率和时偏相关,下面我们来研究在Gardner锁定的过程中,系统的I,Q两路基带信号的星座图的变化。
加入gardner环之后,系统可以有效的克服由发射机和接收机晶振不同导致的误码,通过误码率仿真可知,加入gardner环之后,系统的误码率解决理想值,基本消除了时偏带来的影响。
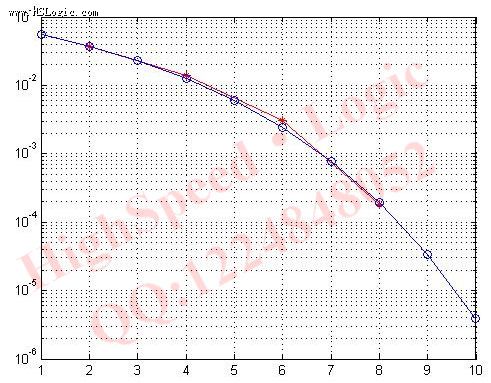
图加Gardner环后的系统误码率曲线仿真图
从仿真可以看到,通过Gardner环之后,其系统误码率基本接近理想值,从而说明采用此方案的正确性。
4.参考文献
两篇经典的Gardner环外文论文:
其余中文参考文献:
《基于FPGA的全数字QPSK通信系统的研究》
《基于FPGA的数字接收机同步技术的研究与实现》
《基于FPGA的数字中频扩频接收机的研究与实现》
《全数字BPSK_QPSK接收机同步技术研究》
最后
以上就是漂亮机器猫最近收集整理的关于gardner环 matlab,HighSpeedLogic专题:位同步Gardner环的研究的全部内容,更多相关gardner环内容请搜索靠谱客的其他文章。








发表评论 取消回复