A*算法简介
该算法是一种全局路径规划算法,结合了贪心算法(深度优先)和Dijkstra算法(广度优先) ,是一种启发式搜索算法根据给定的目标位置和全局栅格地图进行总体路径规划。
A*算法原理
- 将地图虚拟化,并将其划分为一个一个的小方块,这样可以用二维数组来表示地图。(如下图)
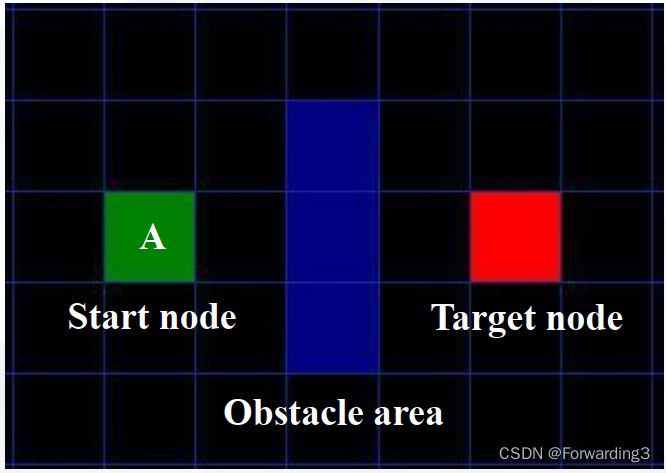
- 。
路径优劣评价公式为:
f ( n ) = g ( n ) + h ( n ) . f(n) = g(n)+ h(n). f(n)=g(n)+h(n).
f(n)是从初始节点经由当前节点n到目标节点的代价估计,g(n)是从初始节点到当前节点n的实际代价,h(n)是从当前节点n到目标节点的最短路径的估计代价。
分别使用了两个状态表,分别称为openList表和closeList表。openList表由待考察的节点组成,closeList表由已经考察过的节点组成。 - 如下图所示:
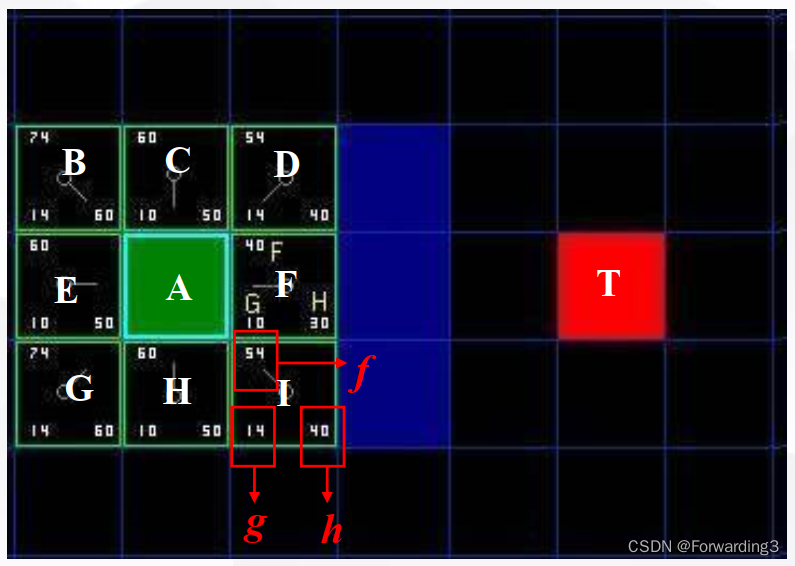
分别 计算A节点周围8个节点的g和h,挑选出最小代价节点F,移动到closelist中。
现在openlist = {B,C,D,E,G,H,I}, closelist = {A,F}. - 从openlist中选择总代价最小的节点I,从openlist中取出,放到closelist中,并把它作为新的父节点。检查所有与它相邻的子节点,忽略障碍物不可走节点、忽略已经存在于closeList的节点; 如果方格不在openList中,则把它们加入到openList中。
- 如果某个节点A已经在open list中,则检查在以当前节点为父节点时,A节点的G是否更优,也就是说经由当前节点(我们选中的节点)到达那个节点是否具有更小的G值。如果没有,不做任何操作。
- 依次类推,不断重复。一旦搜索到目标节点T,完成路径搜索,结束算法。
体会
A*算法本质上是广度优先算法,它将所有有可能成为最短路径的节点都加入到openlist列表中计算,并以预估代价作为启发,从而避免了计算一些绝不可能成为最优路径的节点,与dijskstra相比,更加的“聪明”。
matlab代码实践
child_nodes_cal.m
function child_nodes = child_nodes_cal(parent_node, m, n, obs, closeList)
child_nodes = [];
field = [1,1; n,1; n,m; 1,m];
% 第1个子节点
child_node = [parent_node(1)-1, parent_node(2)+1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 第2个子节点
child_node = [parent_node(1), parent_node(2)+1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 第3个子节点
child_node = [parent_node(1)+1, parent_node(2)+1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 第4个子节点
child_node = [parent_node(1)-1, parent_node(2)];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 第5个子节点
child_node = [parent_node(1)+1, parent_node(2)];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 第6个子节点
child_node = [parent_node(1)-1, parent_node(2)-1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 第7个子节点
child_node = [parent_node(1), parent_node(2)-1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 第8个子节点
child_node = [parent_node(1)+1, parent_node(2)-1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
%% 排除已经存在于closeList的节点
delete_idx = [];
for i = 1:size(child_nodes, 1)
if ismember(child_nodes(i,:), closeList , 'rows')
delete_idx(end+1,:) = i;
end
end
child_nodes(delete_idx, :) = [];
main.m
function child_nodes = child_nodes_cal(parent_node, m, n, obs, closeList)
child_nodes = [];
field = [1,1; n,1; n,m; 1,m];
% 第1个子节点
child_node = [parent_node(1)-1, parent_node(2)+1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 第2个子节点
child_node = [parent_node(1), parent_node(2)+1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 第3个子节点
child_node = [parent_node(1)+1, parent_node(2)+1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 第4个子节点
child_node = [parent_node(1)-1, parent_node(2)];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 第5个子节点
child_node = [parent_node(1)+1, parent_node(2)];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 第6个子节点
child_node = [parent_node(1)-1, parent_node(2)-1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 第7个子节点
child_node = [parent_node(1), parent_node(2)-1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 第8个子节点
child_node = [parent_node(1)+1, parent_node(2)-1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
%% 排除已经存在于closeList的节点
delete_idx = [];
for i = 1:size(child_nodes, 1)
if ismember(child_nodes(i,:), closeList , 'rows')
delete_idx(end+1,:) = i;
end
end
child_nodes(delete_idx, :) = [];
运行结果
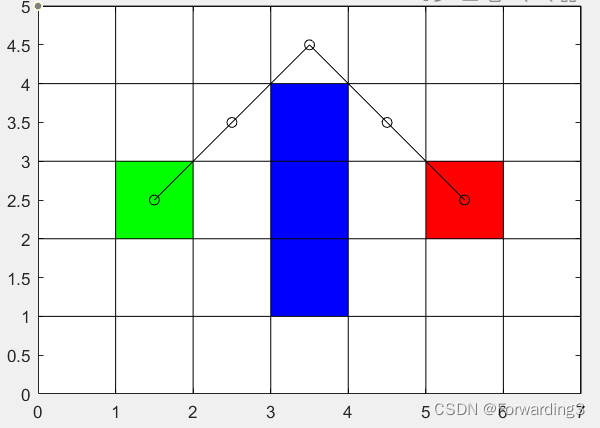
最后
以上就是端庄猎豹最近收集整理的关于A*算法原理与代码实现的全部内容,更多相关A*算法原理与代码实现内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复