1. 首页
  2. 文章中心
  3. c++

A*算法附c++代码一.什么是a*二.算法具体代码

109 阅读 0 评论
我是靠谱客的博主 潇洒衬衫，这篇文章主要介绍A*算法附c++代码一.什么是a*二.算法具体代码，现在分享给大家，希望可以做个参考。

一.什么是a*

一种十分常用的寻路算法，它能够依据某个或某些优化准则，在空间中找到一个从起始点到目标点能避开障碍物的最优路径。

二.算法

以下图为例，敌人要绕过中间的障碍物，寻找到敌人。（以一个方块作为一个节点）
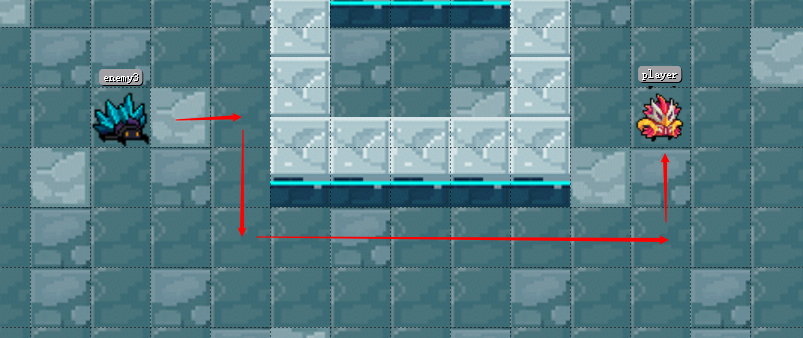
在这里插入图片描述

大概思路

1.首先将敌人所在的节点（起始点）加入到开列表中（接下来可能会用到的节点）
2.从开列表中取出花费值最小的节点（等会会讲到如何求花费值）（当前开列表中就一个节点）作为当前点
3.将当前点加入到闭列表中（已经用过的点，也是最后所需的点）
4.遍历当前点周围的点，搜索能通过的点(不是障碍物以及不在闭列表中)加入到开列表中，将它们的父节点设为当前点（如下图，箭头所指方向即为其父节点）
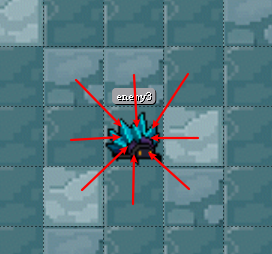
在这里插入图片描述

4.5 稍后讲解
5.跳回到第二步
6.直到遍历当前点周围的点时遇到了玩家（终点），即完成了寻路。
7.从闭列表中最后一个点，向前遍历父节点，即为一条完整的路径

花费值计算

F = G + H
G = 从起点 A 移动到指定方格的移动代价，沿着到达该方格而生成的路径。
H = 从指定的方格移动到终点 B 的估算成本。（可以根据自己的要求去计算，这里选择最简单的方法，H = （终点与起点坐标的x轴的差值+终点与起点坐标的y轴的差值））如下图有红点的节点
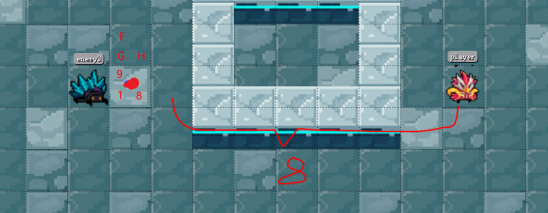
在这里插入图片描述

F = 花费的总值
这个通常被称为试探法，有点让人混淆。为什么这么叫呢，因为这是个猜测。直到我们找到了路径我们才会知道真正的距离，因为途中有各种各样的东西 ( 比如墙壁，水等 ) 。

4.5

当我们遍历当前点周围的点时会遇到一个问题“如果周围的点已经在开列表中怎么办?”
这时我们要重新以当前节点到那个节点的G值，如果小于在开列表里的值则将那个节点的父节点设为当前点并重新计算F值。

具体代码

Astart.h

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#pragma once
/*
A*算法对象类
*/
#include <vector>
#include <list>
#include <functional>
#include "cocos2d.h"
USING_NS_CC;
using namespace std;
#define sqrtTwo 2;

const int straightCost = 1;
const int bevelCost = sqrtTwo;

class CPoint
{
public:
	CPoint(int x,int y)
		:x(x), y(y), F(0), G(0), H(0), parent(nullptr)
	{
		
	}
	~CPoint(){};
	CPoint* parent;
	int x, y;	//横纵坐标
	int F, G, H;	//G起点到当前点的花费，H当前点到终点的花费，F = G+H
};

class Astar
{
public:
	Astar();
	~Astar();
	//初始化地图		1.如果要进行寻路肯定要传地图数据进行
	void initAstar(vector<vector<int>>& maze);
	// 初始化匿名函数，通过外部传进来判断条件（节点能否通过）。
	// 这里因为用的是cocos2d-x，所以参数是vec2类型，可以根据自己的需求调整
	void initFun(function<bool(Vec2)> callBk);
	//	isIgnoreCorner参数是否允许斜角移动	2.开始寻路
	list<CPoint*> GetPath(CPoint &startPoint, CPoint &endPoint, bool isIgnoreCorner);
private:
	//	3.真正进行寻路的算法
	CPoint* findPath(CPoint &startPoint, CPoint &endPoint, bool isIgnoreCorner);
	//	4.获取到当前点周围的点				当前点
	vector<CPoint*> getSurroundPonits(const CPoint* point, bool isIgnoreCorner) const;
	// 5.获取到的点要判断能不能通过
	bool isCanSearch(const CPoint* point, const CPoint* targetPoint, bool isIgnoreCorner) const;
	// 6.还要判断这个点在不在开列表或者闭列表里
	CPoint* isInList(const list<CPoint*>& list, const CPoint* point) const;
	// 7.进行完一次寻路后要取到开列表里最小的f的点
	CPoint* getLeastFPoint();
	// 计算 F G H 的值
	int calcG(CPoint* prePoint, CPoint* point);
	int calcH(CPoint* endPoint, CPoint* point);
	int calcF(CPoint* point);
private:
	//用来判断障碍物
	function<bool(Vec2)> m_callBk;
	list<CPoint*> openList;
	list<CPoint*> closeList;
};

Astart.cpp

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
#include <math.h>
#include "Astar.h"

Astar::Astar()
{
}

Astar::~Astar()
{
}

//初始化回调函数
void Astar::initFun(function<bool(Vec2)> callBk)
{
	m_callBk = callBk;
}


list<CPoint*> Astar::GetPath(CPoint &startPoint, CPoint &endPoint, bool isIgnoreCorner)
{
	//寻路
	CPoint* result = findPath(startPoint, endPoint, isIgnoreCorner);
	list<CPoint*> path;
	//按照起点到终点的顺序放进容器里
	while (result){
		path.push_front(result);
		result = result->parent;
	}
	return path;
}

CPoint* Astar::findPath(CPoint &startPoint, CPoint &endPoint, bool isIgnoreCorner)
{
	//将当前点放入开列表
	openList.push_back(new CPoint(startPoint.x, startPoint.y));
	while (!openList.empty())
	{
		//第一次的话拿到的其实就是起点（startPoint）
		auto curPoint = getLeastFPoint();
		//从开列表中移除
		openList.remove(curPoint);
		//加入到闭列表中
		closeList.push_back(curPoint);
		//获取当前点周围的点
		vector<CPoint*> surroundPoints = getSurroundPonits(curPoint, isIgnoreCorner);
		//遍历周围的点 判断能不能通过
		for (auto& target : surroundPoints)
		{
			//先判断在不在开列表
			if (!isInList(openList, curPoint)){
				//如果不在
				//将当前点设为周围点的父节点
				target->parent = curPoint;
				//计算出target的GHF
				target->G = calcG(curPoint,target);
				target->H = calcH(&endPoint, target);
				target->F = calcF(target);
				//放入到开列表
				openList.push_back(target);
			}
			else{
				//如果在
				int tempG = calcG(curPoint, target);
				//比较G值，选择G值较小的路径，并重新计算F值
				if (tempG < target->G){
					target->parent = curPoint;
					target->G = tempG;
					target->F = calcF(target);
				}
			}
			//判断最终的目标是否被找到
			CPoint* finalPoint = isInList(openList,&endPoint);
			if (finalPoint){
				return finalPoint;
			}
		}
	}
	return nullptr;
}

vector<CPoint*> Astar::getSurroundPonits(const CPoint* point, bool isIgnoreCorner) const
{
	//用临时存放周围的点
	vector<CPoint*> surroundPoints;
	//当前点的左右两边
	for (int i = point->x - 1; i < point->x + 2; i++)
	{
		//当前点的上下两边
		for (int j = point->y - 1; j < point->y + 2; j++)
		{
			CPoint* tempPoint = new CPoint(i, j);
			//判断是否能通过
			if (isCanSearch(point, tempPoint, isIgnoreCorner)){
				//加入到临时容器里
				surroundPoints.push_back(tempPoint);
			}
		}
	}
	//返回周围的点
	return surroundPoints;
}

bool Astar::isCanSearch(const CPoint* point, const CPoint* targetPoint, bool isIgnoreCorner) const
{
	//闭列表里的点不能通过
	if (isInList(closeList, targetPoint) 
		//当前点不能通过
		|| (point->x == targetPoint->x && point->y == targetPoint->y)
		//一些其他的条件，通过外部传入
		|| m_callBk(Vec2(point->x,point->y))) {
		return false;
	}
	// 当前点沿直线行走的点
	if (abs(point->x - targetPoint->x) + abs(point->y - targetPoint->y) == 1){
		return true;
	}
	else{
		//自己设定能否斜角移动
		return isIgnoreCorner;
	}
}

CPoint* Astar::isInList(const list<CPoint*>& list, const CPoint* point) const
{
	//遍历容器
	for (auto p : list){
		if (p->x == point->x && p->y == point->y)
			return p;
	}
	return nullptr;
}

CPoint* Astar::getLeastFPoint()
{
	if (!openList.empty()){
		auto resPoint = openList.front();
		//遍历开列表，返回最小f值的点
		for (auto &point : openList){
			if (point->F < resPoint->F){
				resPoint = point;
			}
		}
		return resPoint;
	}
	return nullptr;
}

int Astar::calcG(CPoint* prePoint, CPoint* point)
{
	//通过判断是否是直线计算花费值
	int exterG = abs(point->x - prePoint->x) + abs(point->y - prePoint->y) == 1 ? straightCost : bevelCost;
	//如果父节点为空，则父节点的值为0
	int parentG = point->parent == nullptr ? 0 : point->parent->G;
	return exterG + parentG;
}

//计算当前点到终点的距离
int Astar::calcH(CPoint* endPoint, CPoint* point)
{
	return abs(point->x - endPoint->x) + abs(point->y - endPoint->y);
}

int Astar::calcF(CPoint* point)
{
	return point->G + point->H;
}

这里附上源码
https://download.csdn.net/download/qq_45620703/19953558
码字不易顺手点个赞。
该文章参考至
https://blog.csdn.net/weixin_44489823/article/details/89382502

最后

以上就是潇洒衬衫最近收集整理的关于A*算法附c++代码一.什么是a*二.算法具体代码的全部内容，更多相关A*算法附c++代码一内容请搜索靠谱客的其他文章。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(72)

相关文章

A*算法（超级详细讲解，附有举例的详细手写步骤）A*寻路算法 拓展
A*算法（超级详细讲解，附有举例的详细手写步骤）A*寻路算法 拓展
知识点二十五：启发式搜索算法——A*算法前言路径搜索问题启发式搜索算法A* 算法解答开篇：如何用A*搜索算法实现游戏中的寻路功能？
知识点二十五：启发式搜索算法——A*算法前言路径搜索问题启发式搜索算法A* 算法解答开篇：如何用A*搜索算法实现游戏中的寻路功能？
A*算法原理与代码实现
A*算法原理与代码实现
A*算法分析及例题介绍一、A*算法的基本原理二、A*算法例题介绍三、例题理论分析四、程序流程图五、启发式函数h(n)的定义六、A*搜索过程中的节点信息七、A*算法与A算法、宽度优先的区别
A*算法分析及例题介绍一、A*算法的基本原理二、A*算法例题介绍三、例题理论分析四、程序流程图五、启发式函数h(n)的定义六、A*搜索过程中的节点信息七、A*算法与A算法、宽度优先的区别
A*算法附c++代码一.什么是a*二.算法具体代码
A*算法附c++代码一.什么是a*二.算法具体代码
启发式搜索算法：A算法（全局、局部择优算法）+A*算法 解决八数码问题1.A 算法2.A*算法
启发式搜索算法：A算法（全局、局部择优算法）+A*算法 解决八数码问题1.A 算法2.A*算法
A星(A*、A Star)路径规划算法详解（附MATLAB代码）
A星(A*、A Star)路径规划算法详解（附MATLAB代码）
寻路算法——A*算法详解并附带实现代码
寻路算法——A*算法详解并附带实现代码

评论列表共有 0 条评论

立即
投稿
返回
顶部