一、A*算法的基本原理

（A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是许多其他问题的常用启发式算法。注意——是最有效的直接搜索算法。

公式表示为： f(n)=g(n)+h(n),其中，
f(n) 是从初始状态经由状态n到目标状态的代价估计，
g(n) 是在状态空间中从初始状态到状态n的实际代价，
h(n) 是从状态n到目标状态的最佳路径的估计代价。
（对于路径搜索问题，状态就是图中的节点，代价就是距离）

h(n)的选取：
保证找到最短路径（最优解的）条件，关键在于估价函数f(n)的选取（或者说h(n)的选取）距离估计与实际值越接近，估价函数取得就越好。
我们以d(n)表达状态n到目标状态的距离，那么h(n)的选取大致有如下三种情况：
1、如果h(n)< d(n)到目标状态的实际距离，这种情况下，搜索的点数多，搜索范围大，效率低。但能得到最优解。
2、如果h(n)=d(n)，即距离估计h(n)等于最短距离，那么搜索将严格沿着最短路径进行， 此时的搜索效率是最高的。
3、如果 h(n)>d(n)，搜索的点数少，搜索范围小，效率高，但不能保证得到最优解。

二、A*算法例题介绍

如下图所示，搜索起点为A，目标点为B的最优路径。注意图中实心方格区域为墙，不可穿越。移动方向仅允许垂直和水平方向移动，每移动一步代价均相同，可设置为1。

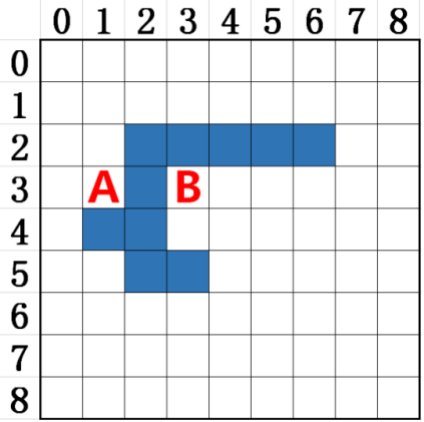
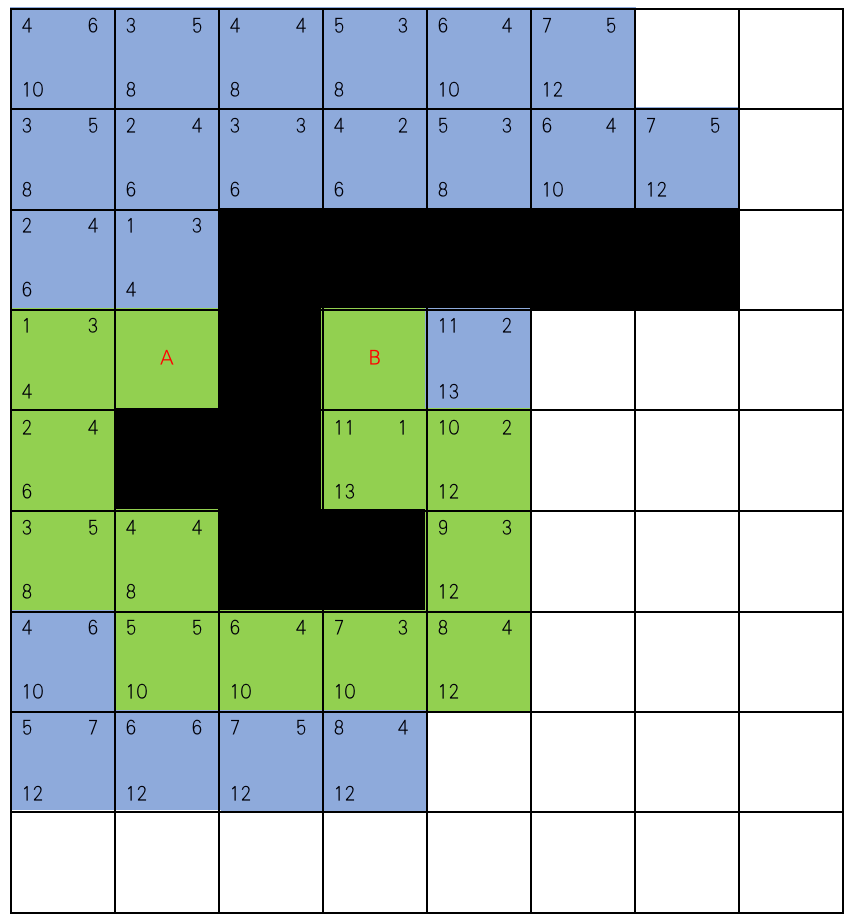
给出搜索过程中每一步中的节点信息（可选择部分中间关键步骤结果进行展示即可）主要包括起点（A）、终点（B）、open表（绿色节点）、closed表（红色节点）、每个节点的计算值（f(n)/g(n)/h(n)）。

三、例题理论分析

该题具体实现可以分为如下步骤：1、设置搜索区域；2、设置open list、close list；3、开始搜索；4、路径排序；5、根据f(n)=g(n)+h(n)继续搜索；6、根据搜索结果确定路径。

1、设置搜索区域：将9*9的表格设置为搜索区域，且将表格中的墙壁设置为不可搜索区域。

2、设置open list、close list：将A及其周围区域放入open list，将每次搜索后的f(n)最小的区域放入close list。

3、开始搜索：从起点A开始进行搜索，根据f(n)=g(n)+h(n)来确定相邻区域的f(n)。

4、路径排序：在步骤二将该点相邻可搜索区域内的点进行搜索完成之后，根据f(n)的大小，对这些区域进行排序。

5、继续搜索：在排好序的区域中选择f(n)最小的区域，继续根据f(n)=g(n)+h(n)来对相邻区域进行搜索。并更新open list 和 close list。

6、若相邻区域已经在open list中(即已经被进行搜索过了)，则从本区域判断其区域f(n)是否可以更新变得更小。

7、不断重复搜索过程，直到将终点B也放入close list中。

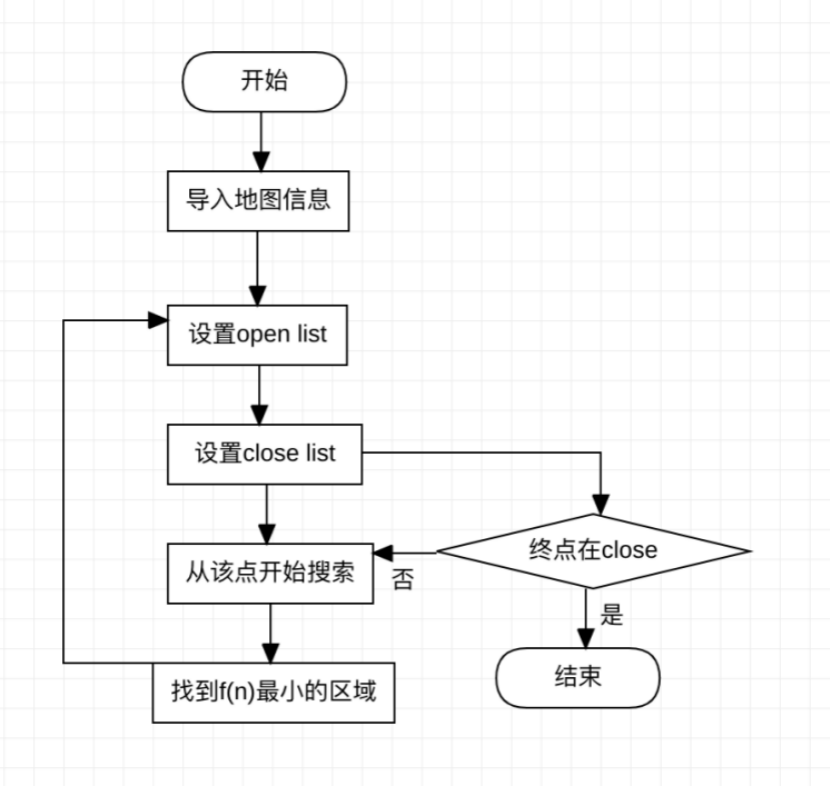
四、程序流程图

五、启发式函数h(n)的定义

static double hManhattanDistance(Point pnt)
{
return Math.abs(pnt.x - END_PNT.x) + Math.abs(pnt.y - END_PNT.y);
}

在实现中，h(n)采用曼哈顿距离，即区域i: (x1,y1)的与区域j: (x2,y2)的距离为：

d(i,j)=|X1-X2|+|Y1-Y2|

六、A*搜索过程中的节点信息

七、A*算法与A算法、宽度优先的区别

1、A*算法解决方案：见上文。

2、宽度优先搜索算法解决方案：

1. 首先将起点放入顺序表中；
2. 从顺序表中读取第一个区域；
3. 对所读取的区域进行相邻区域搜索；
4. 判断相邻区域是否为终点，是终点则停止；
5. 不是终点，则将这些相邻区域放入顺序表；
6. 重复2-5，直到找到终点为止。

最后

以上就是干净烧鹅为你收集整理的A*算法分析及例题介绍一、A*算法的基本原理二、A*算法例题介绍三、例题理论分析四、程序流程图五、启发式函数h(n)的定义六、A*搜索过程中的节点信息七、A*算法与A算法、宽度优先的区别的全部内容，希望文章能够帮你解决A*算法分析及例题介绍一、A*算法的基本原理二、A*算法例题介绍三、例题理论分析四、程序流程图五、启发式函数h(n)的定义六、A*搜索过程中的节点信息七、A*算法与A算法、宽度优先的区别所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。