启发式搜索算法
目录
概念
A算法
A*算法
概念
启发式搜索(Heuristically Search)又称为有信息搜索(Informed Search),它是利用问题拥有的启发信息来引导搜索,达到减少搜索范围、降低问题复杂度的目的,这种利用启发信息的搜索过程称为启发式搜索。
从数据结构与算法的角度去思考这个算法,启发式算法也是贪心算法的一种,启发信息的选取就是贪心策略的选取,倒过来也可以讲,所有的贪心算法也算是状态机中的启发式搜索算法。
用于评价节点重要性的函数称为估价函数,其一般形式为
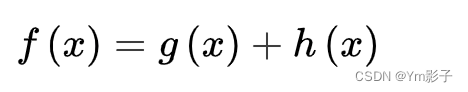
式中:g(x)为从初始节点到节点x付出的实际代价;h(x)为从节点x到目标节点的最优路径的估计代价。启发性信息主要体现在h(x)中,其形式要根据问题的特性来确定。
虽然启发式搜索有望能够很快到达目标节点,但需要花费一些时间来对新生节点进行评价。因此,在启发式搜索中,估计函数的定义是十分重要的。如定义不当,则上述搜索算法不一定能找到问题的解,即使找到解,也不一定是最优的。
A算法
概念
在状态空间搜索中,如果每一步都利用估价函数 f(n)=g(n)+h(n) 对Open表中的结点进行排序,则称A算法。它是一种为启发式搜索算法。
算法类型:
全局择优: 从Open表的所有结点中选择一个估价函数值最小的进行扩展。
局部择优:仅从刚生成的子结点中选择一个估价函数值最小的进行扩展。
算法流程
(全局择优)
- ①将初始节点S0放入Open表中;
- ②如Open表为空,则搜索失败,退出;
- ③把Open表的第一个节点取出,放入到Closed表中,并把该节点记为节点n;
- ④如果节点n是目标节点,则搜索成功,求得一个解,退出;
- ⑤扩展节点n,生成一组子节点,对既不在Open表中也不在Closed表中的子节点,计算出相应的估价函数值;
- ⑥把节点n的子节点放到Open表中;
- ⑦对Open表中的各节点按估价函数值从小到大排列;
- ⑧转到②。
(局部择优)
- ①将初始节点S0放入Open表中;
- ②如Open表为空,则搜索失败,退出;
- ③把Open表的第一个节点取出,放入到Closed表中,并把该节点记为节点n;
- ④如果节点n是目标节点,则搜索成功,求得一个解,退出;
- ⑤扩展节点n,生成一组子节点,对既不在Open表中也不在Closed表中的子节点,计算出相应的估价函数值;
- ⑥对节点n的子节点按估价函数值从小到大排列,选择第一个元素,作为新的节点n,把剩余节点让入open表中;
- ⑦对Open表中的各节点按估价函数值从小到大排列;
- ⑧转到④
对上述算法分析可以发现,如果取估价函数等于节点深度,则它将退化为广度优先搜索。
A*算法
概念
在A*算法中,启发性信息用一个特别的估价函数f*来表示:f*(x)=g*(x)+h*(x)
式中:g*(x)为从初始节点到节点x的最佳路径所付出的代价;h*(x)是从x到目标节点的最佳路径所付出的代价;f*(x)是从初始节点出发通过节点x到达目标节点的最佳路径的总代价。
基于上述g*(x)和h*(x)的定义,对启发式搜索算法中的g(x)和h(x)做如下限制:
①g(x)是对g*(x)的估计,且g(x)>0;
②h(x)是h*(x)的下界,即对任意节点x均有h(x)≤h*(x)。
在满足上述条件情况下的有序搜索算法称为A*算法。
对于某一搜索算法,当最佳路径存在时,就一定能找到它,则称此算法是可纳的。可以证明,A*算法是可纳算法。也就是说,对于有序搜索算法,当满足h(x)≤h*(x)条件时,只要最佳路径存在,就一定能找出这条路径。
距离估计与实际值越接近,估价函数取得就越好
例如对于几何路网来说,可以取两节点间曼哈顿距离做为距离估计,即f=g(n) + (abs(dx - nx) + abs(dy - ny));这样估价函数f(n)在g(n)一定的情况下,会或多或少的受距离估计值h(n)的制约,节点距目标点近,h值小,f值相对就小,能保证最短路的搜索向终点的方向进行。明显优于Dijkstra算法的毫无方向的向四周搜索。
算法流程
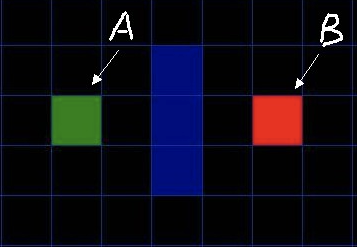
如图所示简易地图, 其中绿色方块的是起点 (用 A 表示), 中间蓝色的是障碍物, 红色的方块 (用 B 表示) 是目的地. 为了可以用一个二维数组来表示地图, 我们将地图划分成一个个的小方块.
二维数组在游戏中的应用是很多的, 比如贪吃蛇和俄罗斯方块基本原理就是移动方块而已. 而大型游戏的地图, 则是将各种"地貌"铺在这样的小方块上.
1. 从起点A开始, 把它作为待处理的方格存入一个"开启列表", 开启列表就是一个等待检查方格的列表.
2. 寻找起点A周围可以到达的方格, 将它们放入"开启列表", 并设置它们的"父方格"为A.
3. 从"开启列表"中删除起点 A, 并将起点 A 加入"关闭列表", "关闭列表"中存放的都是不需要再次检查的方格

图中浅绿色描边的方块表示已经加入 "开启列表" 等待检查. 淡蓝色描边的起点 A 表示已经放入 "关闭列表" , 它不需要再执行检查.
从 "开启列表" 中找出相对最靠谱的方块, 什么是最靠谱? 它们通过公式 F=G+H 来计算.
我们假设横向移动一个格子的耗费为10, 为了便于计算, 沿斜方向移动一个格子耗费是14. 为了更直观的展示如何运算 FGH, 图中方块的左上角数字表示 F, 左下角表示 G, 右下角表示 H. 看看是否跟你心里想的结果一样?
从 "开启列表" 中选择 F 值最低的方格 C (绿色起始方块 A 右边的方块), 然后对它进行如下处理:
4. 把它从 "开启列表" 中删除, 并放到 "关闭列表" 中.
5. 检查它所有相邻并且可以到达 (障碍物和 "关闭列表" 的方格都不考虑) 的方格. 如果这些方格还不在 "开启列表" 里的话, 将它们加入 "开启列表", 计算这些方格的 G, H 和 F 值各是多少, 并设置它们的 "父方格" 为 C.
6. 如果某个相邻方格 D 已经在 "开启列表" 里了, 检查如果用新的路径 (就是经过C 的路径) 到达它的话, G值是否会更低一些, 如果新的G值更低, 那就把它的 "父方格" 改为目前选中的方格 C, 然后重新计算它的 F 值和 G 值 (H 值不需要重新计算, 因为对于每个方块, H 值是不变的). 如果新的 G 值比较高, 就说明经过 C 再到达 D 不是一个明智的选择, 因为它需要更远的路, 这时我们什么也不做.
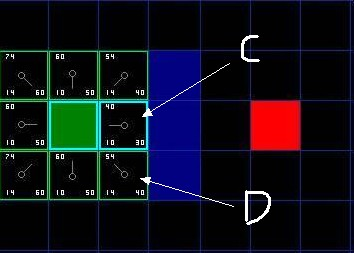
如图, 我们选中了 C 因为它的 F 值最小, 我们把它从 "开启列表" 中删除, 并把它加入 "关闭列表". 它右边上下三个都是墙, 所以不考虑它们. 它左边是起始方块, 已经加入到 "关闭列表" 了, 也不考虑. 所以它周围的候选方块就只剩下 4 个. 让我们来看看 C 下面的那个格子, 它目前的 G 是14, 如果通过 C 到达它的话, G将会是 10 + 10, 这比 14 要大, 因此我们什么也不做.
然后我们继续从 "开启列表" 中找出 F 值最小的, 但我们发现 C 上面的和下面的同时为 54, 这时怎么办呢? 这时随便取哪一个都行, 比如我们选择了 C 下面的那个方块 D.
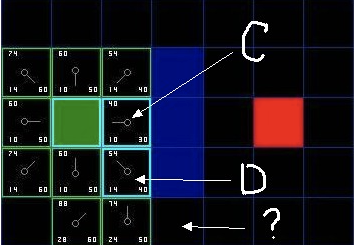
D 右边已经右上方的都是墙, 所以不考虑, 但为什么右下角的没有被加进 "开启列表" 呢? 因为如果 C 下面的那块也不可以走, 想要到达 C 右下角的方块就需要从 "方块的角" 走了, 在程序中设置是否允许这样走. (图中的示例不允许这样走)
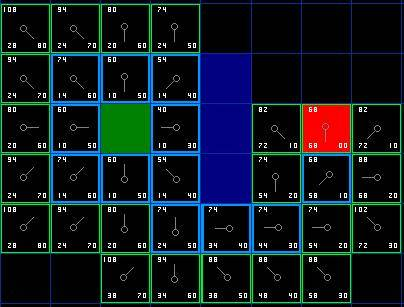
就这样, 我们从 "开启列表" 找出 F 值最小的, 将它从 "开启列表" 中移掉, 添加到 "关闭列表". 再继续找出它周围可以到达的方块, 如此循环下去...
那么什么时候停止呢? —— 当我们发现 "开始列表" 里出现了目标终点方块的时候, 说明路径已经被找到.
如何找回路径
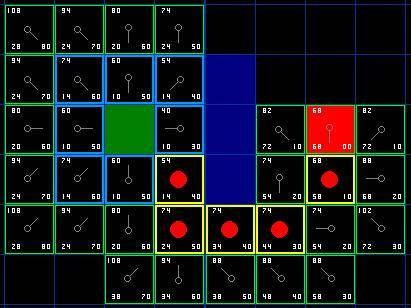
如上图所示, 除了起始方块, 每一个曾经或者现在还在 "开启列表" 里的方块, 它都有一个 "父方块", 通过 "父方块" 可以索引到最初的 "起始方块", 这就是路径.
代码实现
#include <vector>
#include <list>
#include <iostream>
#include <math>
const int kCost1=10; //直移一格消耗
const int kCost2=14; //斜移一格消耗
struct Point
{
int x,y; //点坐标,这里为了方便按照C++的数组来计算,x代表横排,y代表竖列
int F,G,H; //F=G+H
Point *parent; //parent的坐标,这里没有用指针,从而简化代码
Point(int _x,int _y):x(_x),y(_y),F(0),G(0),H(0),parent(NULL) //变量初始化
{
}
};
class Astar
{
public:
void InitAstar(std::vector<std::vector<int>> &_maze);
std::list<Point *> GetPath(Point &startPoint,Point &endPoint,bool isIgnoreCorner);
private:
Point *findPath(Point &startPoint,Point &endPoint,bool isIgnoreCorner);
std::vector<Point *> getSurroundPoints(const Point *point,bool isIgnoreCorner) const;
bool isCanreach(const Point *point,const Point *target,bool isIgnoreCorner) const; //判断某点是否可以用于下一步判断
Point *isInList(const std::list<Point *> &list,const Point *point) const; //判断开启/关闭列表中是否包含某点
Point *getLeastFpoint(); //从开启列表中返回F值最小的节点
//计算FGH值
int calcG(Point *temp_start,Point *point);
int calcH(Point *point,Point *end);
int calcF(Point *point);
private:
std::vector<std::vector<int>> maze;
std::list<Point *> openList; //开启列表
std::list<Point *> closeList; //关闭列表
};
void Astar::InitAstar(std::vector<std::vector<int>> &_maze)
{
maze=_maze;
}
int Astar::calcG(Point *temp_start,Point *point)
{
int extraG=(abs(point->x-temp_start->x)+abs(point->y-temp_start->y))==1?kCost1:kCost2;
int parentG=point->parent==NULL?0:point->parent->G; //如果是初始节点,则其父节点是空
return parentG+extraG;
}
int Astar::calcH(Point *point,Point *end)
{
//用简单的欧几里得距离计算H,这个H的计算是关键,还有很多算法,没深入研究^_^
return sqrt((double)(end->x-point->x)*(double)(end->x-point->x)+(double)(end->y-point->y)*(double)(end->y-point->y))*kCost1;
}
int Astar::calcF(Point *point)
{
return point->G+point->H;
}
Point *Astar::getLeastFpoint()
{
if(!openList.empty())
{
auto resPoint=openList.front();
for(auto &point:openList)
if(point->F<resPoint->F)
resPoint=point;
return resPoint;
}
return NULL;
}
Point *Astar::findPath(Point &startPoint,Point &endPoint,bool isIgnoreCorner)
{
openList.push_back(new Point(startPoint.x,startPoint.y)); //置入起点,拷贝开辟一个节点,内外隔离
while(!openList.empty())
{
auto curPoint=getLeastFpoint(); //找到F值最小的点
openList.remove(curPoint); //从开启列表中删除
closeList.push_back(curPoint); //放到关闭列表
//1,找到当前周围八个格中可以通过的格子
auto surroundPoints=getSurroundPoints(curPoint,isIgnoreCorner);
for(auto &target:surroundPoints)
{
//2,对某一个格子,如果它不在开启列表中,加入到开启列表,设置当前格为其父节点,计算F G H
if(!isInList(openList,target))
{
target->parent=curPoint;
target->G=calcG(curPoint,target);
target->H=calcH(target,&endPoint);
target->F=calcF(target);
openList.push_back(target);
}
//3,对某一个格子,它在开启列表中,计算G值, 如果比原来的大, 就什么都不做, 否则设置它的父节点为当前点,并更新G和F
else
{
int tempG=calcG(curPoint,target);
if(tempG<target->G)
{
target->parent=curPoint;
target->G=tempG;
target->F=calcF(target);
}
}
Point *resPoint=isInList(openList,&endPoint);
if(resPoint)
return resPoint; //返回列表里的节点指针,不要用原来传入的endpoint指针,因为发生了深拷贝
}
}
return NULL;
}
std::list<Point *> Astar::GetPath(Point &startPoint,Point &endPoint,bool isIgnoreCorner)
{
Point *result=findPath(startPoint,endPoint,isIgnoreCorner);
std::list<Point *> path;
//返回路径,如果没找到路径,返回空链表
while(result)
{
path.push_front(result);
result=result->parent;
}
// 清空临时开闭列表,防止重复执行GetPath导致结果异常
openList.clear();
closeList.clear();
return path;
}
Point *Astar::isInList(const std::list<Point *> &list,const Point *point) const
{
//判断某个节点是否在列表中,这里不能比较指针,因为每次加入列表是新开辟的节点,只能比较坐标
for(auto p:list)
if(p->x==point->x&&p->y==point->y)
return p;
return NULL;
}
bool Astar::isCanreach(const Point *point,const Point *target,bool isIgnoreCorner) const
{
if(target->x<0||target->x>maze.size()-1
||target->y<0||target->y>maze[0].size()-1
||maze[target->x][target->y]==1
||target->x==point->x&&target->y==point->y
||isInList(closeList,target)) //如果点与当前节点重合、超出地图、是障碍物、或者在关闭列表中,返回false
return false;
else
{
if(abs(point->x-target->x)+abs(point->y-target->y)==1) //非斜角可以
return true;
else
{
//斜对角要判断是否绊住
if(maze[point->x][target->y]==0&&maze[target->x][point->y]==0)
return true;
else
return isIgnoreCorner;
}
}
}
std::vector<Point *> Astar::getSurroundPoints(const Point *point,bool isIgnoreCorner) const
{
std::vector<Point *> surroundPoints;
for(int x=point->x-1;x<=point->x+1;x++)
for(int y=point->y-1;y<=point->y+1;y++)
if(isCanreach(point,new Point(x,y),isIgnoreCorner))
surroundPoints.push_back(new Point(x,y));
return surroundPoints;
}
using namespace std;
int main()
{
//初始化地图,用二维矩阵代表地图,1表示障碍物,0表示可通
vector<vector<int>> maze={
{1,1,1,1,1,1,1,1,1,1,1,1},
{1,0,0,1,1,0,1,0,0,0,0,1},
{1,0,0,1,1,0,0,0,0,0,0,1},
{1,0,0,0,0,0,1,0,0,1,1,1},
{1,1,1,0,0,0,0,0,1,1,0,1},
{1,1,0,1,0,0,0,0,0,0,0,1},
{1,0,1,0,0,0,0,1,0,0,0,1},
{1,1,1,1,1,1,1,1,1,1,1,1}
};
Astar astar;
astar.InitAstar(maze);
//设置起始和结束点
Point start(1,1);
Point end(6,10);
//A*算法找寻路径
list<Point *> path=astar.GetPath(start,end,false);
//打印
for(auto &p:path)
cout<<'('<<p->x<<','<<p->y<<')'<<endl;
system("pause");
return 0;
}最后
以上就是想人陪小天鹅最近收集整理的关于算法提升:图的启发式搜索算法(A算法、A*算法)的全部内容,更多相关算法提升:图内容请搜索靠谱客的其他文章。








发表评论 取消回复