一道图论神题(god)
Time Limit:1000ms Memory Limit:128MB
题目描述
LYK有一张无向图G={V,E},这张无向图有n个点m条边组成。并且这是一张带权图,只有点权。
LYK想把这个图删干净,它的方法是这样的。每次选择一个点,将它删掉,但删这个点是需要代价的。假设与这个点相连的还没被删掉的点是u1,u2,…,uk。LYK将会增加a[u1],a[u2],…,a[uk]的疲劳值。
它想将所有点都删掉,并且删完后自己的疲劳值之和最小。你能帮帮它吗?
输入格式(god.in)
第一行两个数n,m表示一张n个点m条边的图。
第二行n个数ai表示点权。
接下来m行每行三个数u,v,表示有一条连接u,v的边。数据保证任意两个点之间最多一条边相连,并且不存在自环。
输出格式(god.out)
你需要输出这个最小疲劳值是多少。
输入样例
输出样例
404 3
10 20 30 40
1 4
1 2
2 3
样例解释
一个合理的方法是先删4号点,此时有10点疲劳值。接下来删3号点,获得20点疲劳值,再删2号点,获得10点疲劳值,最后删1号点,没有疲劳值。总计40点疲劳值。
对于30%的数据n<=10。
对于60%的数据n,m<=1000。
对于100%的数据1<=n,m,ai<=100000
贪心,最开始写了个以每个点的删去以后的代价的贪心,结果发现样例都过不了。然后就该了种贪心的方法、、、
对于每个点不删去的话他会对删去其他的点造成它的点权的影响,我们要使代价降到最小,那么我们要先将这个造成影响最大的点删掉,这样在删其他的点时就先把这个代价最大的部分去掉了,这样应该是最优的·
#include<cstdio> #include<vector> #include<cstring> #include<iostream> #include<algorithm> #define N 100010 #define LL long long using namespace std; bool vis[N]; long long ans; int n,m,x,y,w[N],sum[N]; vector<int>vec[N]; int read() { int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar(); return x*f; } struct Node { int w,num; }a[N]; int cmp(Node a,Node b){return a.w>b.w;} int main() { freopen("god.in","r",stdin); freopen("god.out","w",stdout); n=read(),m=read(); for(int i=1;i<=n;i++) a[i].w=read(),a[i].num=i,w[i]=a[i].w; for(int i=1;i<=m;i++) { x=read(),y=read(); vec[x].push_back(y),vec[y].push_back(x); } sort(a+1,a+1+n,cmp); for(int i=1;i<=n;i++) { x=a[i].num;vis[x]=true; for(int j=0;j<vec[x].size();j++) if(!vis[vec[x][j]]) ans+=(LL)w[vec[x][j]]; } printf("%I64d",ans); return 0; }
位运算2(bit)
Time Limit:1000ms Memory Limit:128MB
题目描述
LYK拥有一个十进制的数N。它赋予了N一个新的意义:不考虑N的符号,将N每一位都拆开来后再加起来就是N所拥有的价值。例如数字123拥有6的价值,数字999拥有27的价值,数字-233拥有8的价值。
假设数字N的价值是K,LYK想找到一个价值是K+1的数字,当然这个答案实在太多了,LYK想使得这个价值为K+1的数字尽可能大,并且需要保证这个数字小于N。
输入格式(bit.in)
一个整数N。
输出格式(bit.out)
一个数表示答案。你需要输出一个整数,且这个数不包含前导0。
输入样例1
199
输出样例1
-299
输入样例2
1520
输出样例2
1512
对于20%的数据|N|<=10
对于40%的数据|N|<=100
对于60%的数据|N|<=10^9
对于80%的数据|N|<=10^1000
对于100%的数据|N|<=10^100000。
啊啊啊,得了40分,然后改了一个小时以后才把它改成50、、、(呜呜)
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define N 100010 #define maxn 0x7fffffff using namespace std; bool flag; char a[N]; int q,s,num1,num2,minn=maxn; int main() { freopen("bit.in","r",stdin); freopen("bit.out","w",stdout); cin>>a;int l=strlen(a); if(a[0]=='-') s=1; else s=0; for(int i=l-1;i>=s;i--) { if(a[i]<'9'&&minn==maxn) { if(a[i]!='0') a[i]++; num1=i,minn=a[i]; } if(a[i]>minn) if(minn!=48){q=a[i],a[i]=minn,flag=true,a[num1]=q,num2=i; break;} else {a[i]++,flag=true,num2=i;break;} } if(flag) { if(minn=='0') { if(num2==0) for(int i=0;i<l-num2-1;i++) cout<<a[i]; else { q=a[num1],a[num1]=a[num2],a[num2]=q; for(int i=0;i<=num1;i++) cout<<a[i]; } } else for(int i=0;i<l;i++) cout<<a[i]; } else if(a[0]=='-') { if(minn!=maxn)for(int i=0;i<l;i++) cout<<a[i]; else { printf("-1"); for(int i=1;i<l;i++) cout<<a[i]; } } else { printf("-"); for(int i=0;i<l;i++) cout<<a[i]; } return 0; }
分类讨论
分为正数和负数两种情况,当为负数时,最优解一定是倒着数第一个不为9的数+1
当为正数时,又有两种情况,一种是答案为正数,一种是答案为负数。
我们先找到除最后一个数以外第一个(倒着)大于0的数,如果这个数往后的数都大于8并且8的个数小于1个,那么这个数不满足条件,因为如果这样的话我们后面没法使后面的位置总共加上2(因为要价值+1,那么原数的每位数的和就要+1,并且我们找到的这个合法的位置上的数要-1所以后面的数的和要比原数多2),这样我们就继续往前找,找到一个合法的位置,让这个位置上的数-1,前面的数不变,后面的数最高位上尽量放最大的数,但是这个数的和等于sum,如果没有数了就补零
#include<cstdio> #include<cstring> #include<cstdlib> #include<iostream> #include<algorithm> #define N 100010 using namespace std; bool flag; char ch[N]; int t,num[N]; int main() { // freopen("bit.in","r",stdin); // freopen("bit.out","w",stdout); cin>>ch+1; int l=strlen(ch+1),s=1; if(ch[1]=='-')//分类讨论,为负数的情况,这种情况比较好做,我们找到第一个小于9的位置,这个位置上的数+1,然后其余的不变,这就是最小值, { for(int i=l;i>s;i--)//找到第一个小于9的位置 if(ch[i]<'9') {ch[i]++,flag=true;break;} //+1 if(!flag) ch[1]='1',ch[0]='-',s=0;//判断是否在原序列中找到这样的位置,如果不能,我们要在最前面+1 for(int i=s;i<=l;i++) cout<<ch[i]; } else//正数 ,我们需要找到除最后一个数以外第一个(这里为倒着的)大于零的数,然后使这个-1,这个位置前面的数不变,后面的数按最高位上放最大的,没有可以放的数时补零 { for(int i=1;i<=l;i++) num[i]=ch[i]-'0'; int sum=num[l]+2,s; for(int i=l-1;i>=1;i--)//我们可能会遇到这样的情况例如99,98,998我们在第一个不为零得数上-1后面的数加不开了怎么办,这样的话一定是输出负数,且为在这个数前面多了一个1 { if(num[i]!=0) //找第一个不为零的数 { if(num[i+1]==9||(num[i+1]==8&&t==0)) {if(num[i+1]==8) t++;sum+=num[i];}//上面的那种情况对于329这样的书就不满足条件了,这样我们要找第二个大于0的数并且这个数往后最小的数一定不为9,8为最小的话至少两个8,然后在进行操作 else {flag=true,num[i]--,s=i;break;} } else sum+=num[i]; } if(!flag) { printf("-"); if(num[l]==9) { printf("1"); for(int i=1;i<=l;i++) cout<<num[i]; } else //当为98这种数时我们的结果为-99 { num[l]++; for(int i=1;i<=l;i++) cout<<num[i]; } } else { flag=false; while(sum) { num[++s]=min(sum,9); sum-=min(sum,9); } for(int i=1;i<=s;i++) if(num[i]>0||flag) flag=true,printf("%d",num[i]); for(int i=s+1;i<=l;i++) printf("0"); } } return 0; }
逆序对(pair)
Time Limit:1000ms Memory Limit:128MB
题目描述
LYK最近在研究逆序对。
这个问题是这样的。
一开始LYK有一个2^n长度的数组ai。
LYK有Q次操作,每次操作都有一个参数k。表示每连续2^k长度作为一个小组。假设n=4,k=2,则a[1],a[2],a[3],a[4]为一个小组,a[5],a[6],a[7],a[8]为一个小组,a[9],a[10],a[11],a[12]为一个小组,a[13],a[14],a[15],a[16]也为一个小组。
然后LYK对于每个小组都翻转,也就是说原数组会变成a[4],a[3],a[2],a[1],a[8],a[7],a[6],a[5],a[12],a[11],a[10],a[9],a[16],a[15],a[14],a[13]。之后它想求出这2^n个数的逆序对是多少。
因此你需要输出对于每次操作,操作完后这2^n个数的逆序对有多少对。
两个数ai,aj被称为逆序对当且仅当i<j且ai>aj。
输入格式(pair.in)
第一行一个数n。
接下来一行2^n个数ai表示一开始的数组。
接下来一行一个数Q,表示操作的次数。
接下来一行Q个数,表示每次操作的参数k。
输出格式(pair.out)
Q行,表示每次操作后的答案。
输入样例
2
2 1 4 3
4
1 2 0 2
输出样例
0
6
6
0
样例解释
第一次操作,{2,1,4,3}->{1,2,3,4}
第二次操作,{1,2,3,4}->{4,3,2,1}
第三次操作,{4,3,2,1}->{4,3,2,1}
第四次操作,{4,3,2,1}->{1,2,3,4}
对于30%的数据n<=10,Q<=10。
对于50%的数据n<=10,Q<=1000。
对于80%的数据n<=10,Q<=200000。
对于100%的数据n<=17,Q<=200000,1<=ai<=2^n。
还有不知道怎么求逆序对的童鞋吗?http://www.cnblogs.com/z360/p/6921604.html(对逆序对了解不是很清楚的可以看一下这个博客)
又不懂st表的同学吗?http://m.blog.csdn.net/BerryKanry/article/details/70177006(st表讲解)
把1左移m位,相当于1扩大了2^m
(参考博客http://www.cnblogs.com/TheRoadToTheGold/p/7638794.html)
例:1 2 3 4 5 6 7 8 k=3
翻转结果为 8 7 6 5 4 3 2 1
将翻转过程拆分:
第一步: 2 1 4 3 6 5 8 7
第二步:4 3 2 1 8 7 6 5
第三步:8 7 6 5 4 3 2 1
所以每一次翻转都可以拆分,而拆分的过程就是交换相邻的2^(步数-1)
所以归并排序求逆序对的时候,用st表维护从第i个位置,长为2^j的区间的逆序对个数
然后求出对应区间的顺序对个数
维护所有长为2^i的区间的逆序对个数rev[i]和顺序对个数pos[i]
统计答案的时候,拆分就是swap(rev,pos)
在这里顺序对个数是用总个数-逆序对个数求的
所以就会有一个问题,例:
2 2 3 3
实际上的:
pos : 0 0
rev : 0 0
但求的时候,pos :2 4
因为用总个数-逆序对个数=顺序对个数+相等的数对
所以归并过程中,还要预处理从第i个位置,长为2^j的区间的相等数对个数
计算rev,pos时,同时计算same[i],表示所有长为2^i的区间相等的数对个数
求解的时候 先swap(rev,pos),然后rev-=same,再 pos=总的-rev
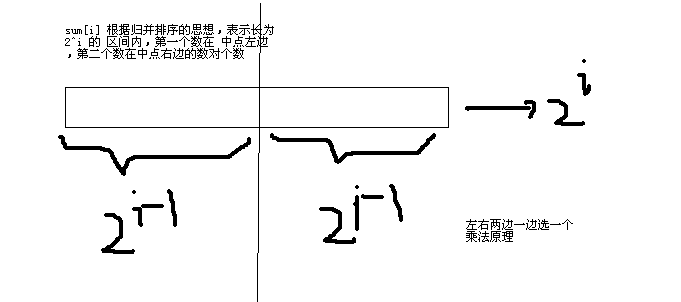
分析详见代码
#include<cstdio> #include<cstring> #include<cstdlib> #include<iostream> #include<algorithm> #define N (1<<17)+10 #define LL long long using namespace std; int n,Q,x,tot,a[N],P[N],tmp[N],bit[N]; LL ans,ni[N],sum[N],shun[N],same[N],st[N][20],ST[N][20]; int read() { int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar(); return x*f; } void qsort(int l,int r)//求逆序对,逆序对的求法都会吧?不会的直接去哪个链接里面看吧 { if(l==r) return; int mid=(l+r)>>1; qsort(l,mid); qsort(mid+1,r); for(int i=r;i>=l;i--) P[i]=i;//p赋初值,P数组表示的是一段连续的区间内相同的数的最大标号。 for(int i=r-1;i>=l;i--) if(a[i]==a[i+1]) P[i]=P[i+1]; int i=l,j=mid+1,k=l; while(i<=mid&&j<=r)//归并排序,先左边的跟右边的比较大小,在一边的没有了以后在直接把另一边的复制到tmp数组中,tmp数组是我们已经排好序的数组 {//归并排序是基于二分的思想,先将小的区间合并然后在合并大的区间,也就是说我们在合并一个大的区间的时候他的左右这两段小区间是已经排好序的 if(a[i]<a[j]) tmp[k++]=a[i++];//前面的数小于后面的数,对逆序对的个数没有影响 else if(a[i]==a[j]) ST[l][bit[r-l+1]]+=P[j]-j+1,tmp[k++]=a[i++]; //统计区间内的数相等的区间,ST数组储存的是以i为开头的,长度为r-l+1的相同的区间, //为什么个数为P[j]-j?p[j]为是当前数的最大的在数组内的编号,这一段数的个数为p[j]-j这些数可以和a[i]组成相等的区间 else st[l][bit[r-l+1]]+=mid-i+1,tmp[k++]=a[j++]; //st数组储存的是以i为开头的,长度为r-l+1的区间内的逆序对的个数,如果a[i]比a[j]大说明i后面的所有的数都会比j大,那么能组成的逆序对的个数即为mid-i+1 } while(i<=mid) tmp[k++]=a[i++]; while(j<=r) tmp[k++]=a[j++]; for(k=l;k<=r;k++) a[k]=tmp[k]; } int work() { for(int i=1;i<=n;i++) sum[i]=1LL*(1<<i-1)*(1<<i-1);//sum数组表示长为i的区间的,i小于mid,j大于mid的区间的个数 for(int i=1,len=2;i<=n;i++,len<<=1)//2^i为区间的长度,也就是len for(int j=1;j<=tot;j+=len)//j为区间的头结点 ni[i]+=st[j][i],shun[i]+=sum[i]-st[j][i],same[i]+=ST[j][i];//ni表示在长度为2^i区间里的逆序对的个数,shun为顺序对的个数,顺序对的个数等于总区间的个数减去逆序对的个数 } int main() { freopen("pair.in","r",stdin); freopen("pair.out","w",stdout); n=read(),tot=1<<n; for(int i=2;i<=tot;++i) bit[i]=bit[i>>1]+1;//bit数组储存的是2^bit[i]=i,也就是lg i的大小,为什么要处理一个bit数组?因为我们在后面要用st表记录一段区间内的逆序对的个数,而st表的st[i][j]表示以i为头结点,以2^j为结尾的一段区间 for(int i=1;i<=tot;++i) a[i]=read(); qsort(1,tot);work();//求逆序对以及处理逆序对的个数 Q=read(); while(Q--) { x=read();ans=0;//总个数-逆序对的个数=顺序对的个数,逆序对的个数=顺序对的个数-相同的个数 for(int i=1;i<=x;i++) swap(ni[i],shun[i]),ni[i]-=same[i],shun[i]=sum[i]*tot/(1<<i)-ni[i];//对于每一个反转,我们都可以将其拆分成交换相邻的2^(步数-1) for(int i=1;i<=n;i++) ans+=ni[i];//统计答案 printf("%I64dn",ans); } return 0; }

距 NOIp2017 还剩 29 天
你可以做的事情还有很多,即使到最后一秒也不要放弃,因为不到结束的那一刻谁也不知道结果会怎样。
转载于:https://www.cnblogs.com/z360/p/7649217.html
最后
以上就是烂漫铃铛最近收集整理的关于10.1综合强化刷题 Day2 morning的全部内容,更多相关10.1综合强化刷题内容请搜索靠谱客的其他文章。








发表评论 取消回复