（已转首都师范大学汇编，该记录停更）

日志：2022.03.04 first

汇编语言程序设计_电子科技大学_中国大学MOOC(慕课)

学习课程链接 ↑

目录

概念

学习目的

进位计数制及其相互转换

二进制和十进制的互相转换

01.十进制整数转换为二进制数

001.减权定位法

002.除基取余法

02.十进制小数转换为二进制数

001.减权定位法

002.乘基取整法

03.二进制整数转换为十进制数

 001.按权相加法

 002.逐次乘基相加法

 04.二进制小数转换为十进制数

001.按权相加法

 002.逐次除基相加法

带符号数的表示

原码表示

补码

意义

定义

由真值、原码变换为补码

 补码数的表示范围

补码的加减运算

字符的表示

基本逻辑运算

几种常见的基本逻辑运算

概念

汇编语言是为了便于记忆和阅读，使用字母和符号来表示机器语言的命令，用十进制数或十六进制数来表示数据的计算机程序设计语言。

汇编语言的语句与机器语言指令一一对应，汇编语言程序与机器语言程序效率相同

注意，不同类型计算机有不同的机器指令系统和汇编语言描述。

学习目的

1. 学习和使用汇编语言可以从根本上认识、理解计算机的工作过程。

2.可以更充分地利用机器硬件的全部功能，发挥机器的长处。

3. 机器自检、系统初始化、实际的输入输出设备等等操作必须使用汇编语言。

4. 汇编语言程序的效率高于高级语言程序。

5. CTF小白必学

6. ……

4 中“效率”有两个方面的含义：程序的目标代码长度和运行的速度。在某些要求节省内存空间和提高程序运行速度的应用场合，如实时过程控制、智能仪器仪表等，常常用汇编语言来编制程序。

进位计数制及其相互转换

进位计数制是使用一定个数的数码的组合来表示数字的表示方法。

不同的进位计数制使用的“数码”的数量不同。

不同的进位制和不同的位置其位权是不同的。

位权乘以对应位置上的数码就等于该数位上数值的大小。

如：十进制数，用0、1、2、…… 8、9 十个数码的组合来表示数字。

每个数码所表示的数值大小和其所在的位置相关。

例如：123这个数，个位的3代表3个1，十位的2代表2个10，百位的1代表1个100.

位权（简称：位）是 各个位置上所表示的基本数值。

基数 是 每个数位上能使用不同数码的个数。

如：

十进制有十个数码 0～9，基数为10；

二进制基数为2。

每个数位能取的最大数码值=基数-1。（如十进制为10-1=9）

因为在计算机中最容易被表示和存储，且适合于逻辑值的表达与运算，在计算机中数据表示一般采用二进制数，但是对人来说二进制不便于书写和阅读，因此书写时常使用10进制、8进制和16进制。

其中二进制与8进制、16进制的转换关系：

3位二进制数与一位8进制数对应，4位二进制数与一位16进制数对应。

为了区别，在数的尾部用一个字母来表示不同的进位计数制

B（Binary）                 ——二进制数
O (Octal)或Q                ——八进制数
D (Decimal)                  ——十进制数
H (Hexadecimal)          ——十六进制数。
未使用字母，则默认表示为 十进制

二进制和十进制的互相转换

01.十进制整数转换为二进制数

001.减权定位法

从二进制数高位起，依次用待转换的十进制数与各位权值进行比较，如够减，则该数位系数Ki=1，同时减去该位权值，余数作为下一次比较的值；如不够减，则Ki=0 ；（是不是没看懂，没事，我自己也看不懂，直接看例子就明白了）

例：将325转换为二进制数，直到余数为0。

首先确定二进制数的最高位

因为 2^9 = 512 > 325 > 2^8 = 256，因此从K8位开始比较

减数比较	ki	对应二进制数
325-256=69	k8	1
69<128	k7	0
69-64=5	k6	1
5<32	k5	0
5<16	k4	0
5<8	k3	0
5-4=1	k2	1
1<2	k1	0
1-1=0	k0	1

所以 325D=101000101B

002.除基取余法

将十进制数除以基数2，其余数为二进制数的最低位，再用其商除2，其余数为次低位，反复做下去，直到商等于0.

02.十进制小数转换为二进制数

001.减权定位法

转换时应根据程序要求的精度或计算机的字长来确定二进制的位数。

减权比较	Ki	对应二进制数
0.645 - 0.5 = 0.145	k-1	1
0.145 < 0.25 (0.5^2)	k-2	0
0.145 - 0.125 = 0.02	k-3	1
0.02 < 0.0625  (0.5^4)	k-4	0
0.02<0.03125	k-5	0
0.02-0.015625	k-6	1

所以 0.645D=0.101001B

002.乘基取整法

例 将0.8125D转换为二进制数

乘以基数	Ki	整数部分
0.8125×2＝1.625	k-1	1
0.625×2＝1.25	k-2	1
0.25×2＝0.5	k-3	0
0.5×2＝1.0	k-4	1

所以 0.8125D＝0.1101B

03.二进制整数转换为十进制数

 001.按权相加法

例：101000101B＝1×2^8＋1×2^6＋1×2^2＋1×2^0
                            ＝256＋64＋4＋1
                            ＝325

 002.逐次乘基相加法

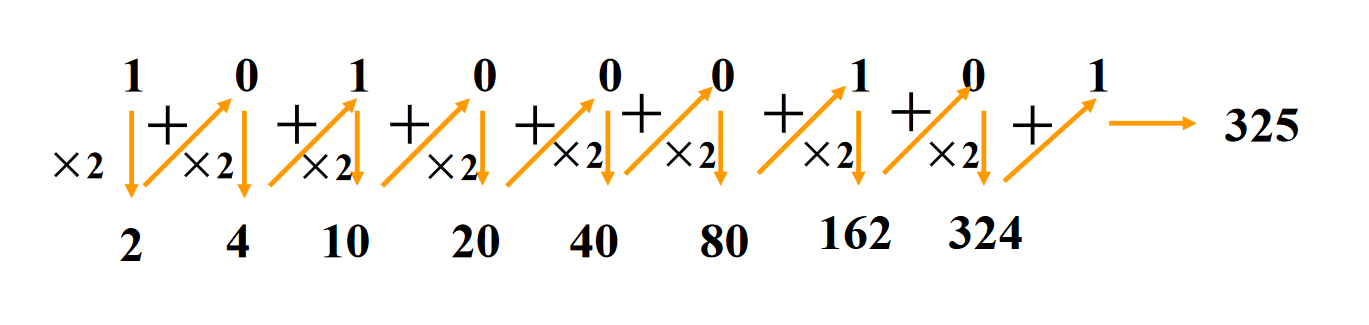
 04.二进制小数转换为十进制数

001.按权相加法

例: 0.101001B   = 1×2-1＋1×2-3＋1×2-6
                        ＝0.5+0.125+0.0156
                        ＝0.640625D

 002.逐次除基相加法

说白了就是先 除以2， 再加上上面的0或者1（0的时候也就等于不加），然后再将相加后的结果除以2，如此往复。

带符号数的表示

一般算术中使用”“+”和“-”来表示正数与负数            在计算机中则使用“0”和“1”来表示正数和负数

用“＋”或“－”表示正负的数叫真值                           用“0”或“1”表示正负的数叫机器数

带符号的机器数可以用 原码、反码和补码 三种不同码制来表示。

一般计算机中大多采用补码表示。

原码表示

二进制数的最高位表示符号，0表示正，1表示负。数值部分用二进制数绝对值表示。

8位二进制数原码的          最大数为    01111111  （+127）
                                         最小数为    11111111  （-127）
8位二进制数表示范围      －127 ≤ X ≤ +127

0的原码有两种表示形式：00000000和10000000（+0和-0）

补码

补码_百度百科

意义

        补码“模”概念的引入、负数补码的实质、以及补码和真值之间的关系所揭示的补码符号位所具有的数学特征，无不体现了补码在计算机中表示数值型数据的优势，和原码、反码等相比可表现在如下方面

(1)解决了符号的表示的问题

(2)可以将减法运算转化为补码的加法运算来实现，克服了原码加减法运算繁杂的弊端，可有效简化运算器的设计

(3)在中计算机中利用电子器件的特点实现补码和真值、原码之间的相互转换，非常容易

(4)补码表示统一了符号位和数值位，使得符号位可以和数值位一起直接参与运算，这也为后面设计乘法器、除法器等运算器件提供了极大的方便。总之，补码概念的引入和当时运算器设计的背景不无关系，从设计者角度，既要考虑表示的数的类型 (小数、整数、实数和复数)、数值范围和精确度，又要考虑数据存储和处理所需要的硬件代价。因此，使用补码来表示机器数并得到广泛的应用，也就不难理解了。

反正意思就是计算机用补码更好，效率更高

定义

带符号数X的补码表示 [X]补 定义为：

​

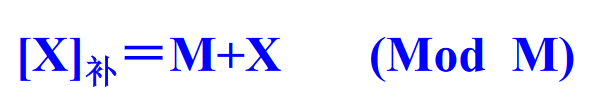
      其中模数M根据机器数的位数而定，如位数为8则M=2^8,用补码表示的机器数，符号位仍然表示数的符号：0为正,1为负。对于正数，补码与原码相同，对于负数需要进行变换。

由真值、原码变换为补码

负数的 真值 变换为 补码：        将                          各位取反，然后 最低位加1。
负数的 原码 变换为 补码：        保持符号位不变， 其余各位变反， 最低位加1。

​

 补码数的表示范围

当位数为8时，  最大补码为        01111111  = [+127]补
                          最小补码为        10000000 = [-128]补

0 的补码只有一个，[0]补 = 00000000，10000000 是  [-128]补，11111111  是  [-1]补

对于当位数为16时，补码表示范围是  -32768  ~  +32767

补码的加减运算

​

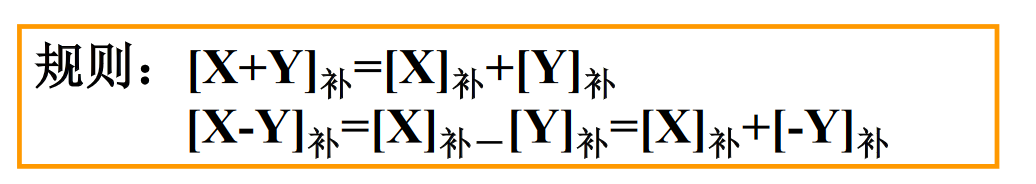
其中 [-Y]补 是对 [Y]补 执行一次求补运算 

求补运算 是 将原数 连同符号位一起（不管是正还是负）按位求反，再在最低位加1

加法运算：

​

减法运算：

​

因为这个 计算过程 对 格式 的要求太高了，就偷懒截图了……; )

过程很好理解……

字符的表示

在计算机内部，各种字符（字母、符号、数字码）都是按一定的方式编写成二进制信息。不同的计算机以及不同的场合所采用的编码方式可能是不一样的。

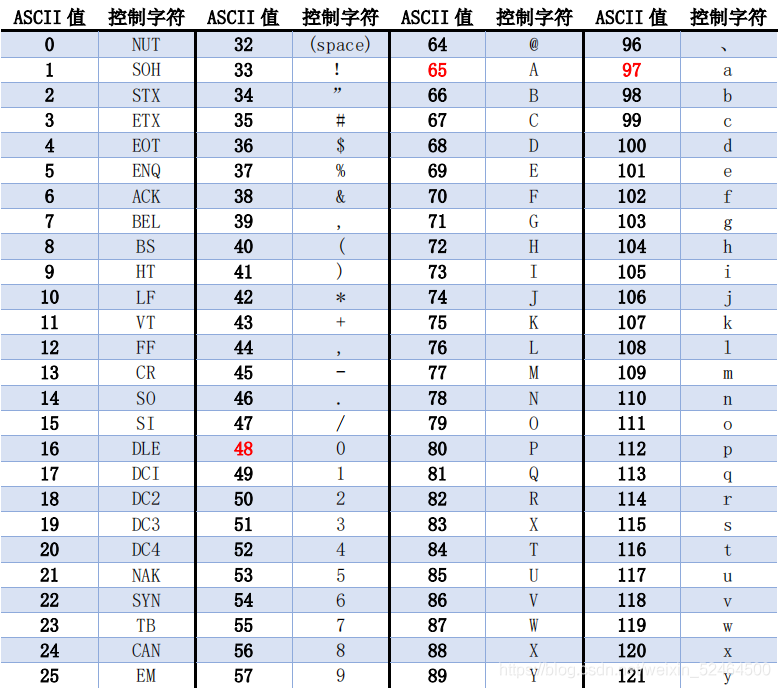
最广泛采用的是 ASCII 码 （American Standard Code for Information Interchange）

标准ASCII码为一字节，其中用低七位表示字符编码, 用最高位表示奇偶数验位

​

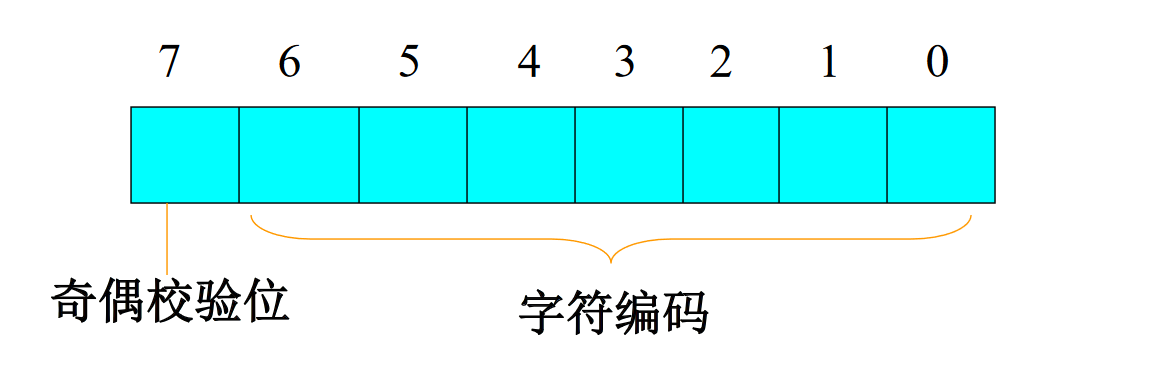
 标准ASCII码共有128个，可分为两类：

非打印ASCII码共33个，用于控制操作, 如BEL(响铃07H),DEL(删除7FH),CR(回车,0DH)。

可打印ASCII码共95个，如数字符0~9，大小写字母等。

ASCII表

​

基本逻辑运算

计算机内部采用二进制数表示信息，具有物理实现容易、可靠性高的优点，且由于状态“0”和“1”正好与逻辑运算中的逻辑“真”和“假”对应，因此可以用“0”和“1”来表示逻辑变量的取值，很容易地实现各种复杂的逻辑运算。

几种常见的基本逻辑运算

与

或

非

异或

……

都是上学期学C语言的时候就应该要掌握的东西

最后

以上就是纯真镜子最近收集整理的关于汇编语言 学习记录（详细）汇编语言程序设计_电子科技大学_中国大学MOOC(慕课) 概念 学习目的 进位计数制及其相互转换 二进制和十进制的互相转换  带符号数的表示 字符的表示基本逻辑运算的全部内容，更多相关汇编语言内容请搜索靠谱客的其他文章。