数字逻辑基础
数制
数制:数的表示方法,包括基数和位权。比如十进制、二进制、十六进制等。
基数:一个数位上可能出现的数码的个数,比如十进制的基数为0、1、2、3、4、5、6、7、8、9,基数R=10
位权:基数的幂,比如十进制137=1*10^2+3 *10^1+7 *10^0。
数制之间的相互转换
除基取余法:适用于将十进制数的整数部分转换成其他进制的数
例子如下:

乘基数取整法:适用于将十进制数的小数部分转换成其他进制的数
例子如下:

综合练习,求解一下:
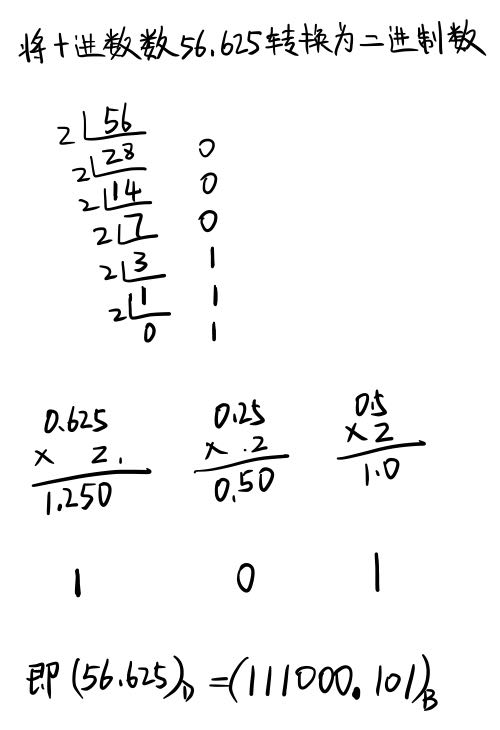
按位权展开相加法:适合于非十进制数转换成十进制数。
例子如下:

分组法:适合于二进制、八进制、十六进制之间的相互转换。
例子如下:

码制
一定规律排列的多位二进制数码表示某种信息,称为编码。形成代码的规律法则,称为码制。n位二进制可有2^n种不同的组合,可以代表2^n种不同的信息,以下是几种常见的编码方法:
二-十进制编码:用四位二进制数码表示一位十进制数的代码,BCD码。
有权码:每一位都有固定的权值。
无权码:每一位都没有固定的权值。
奇偶校验码:是一种可以检测出一位错误的代码,由信息位和校验位组成。
三种基本逻辑运算
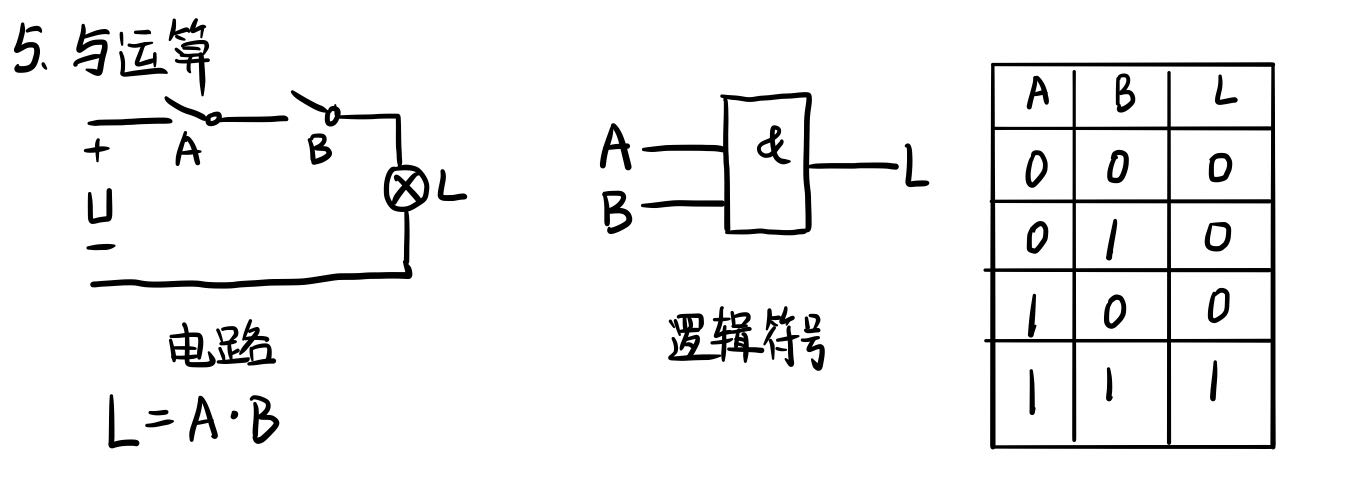
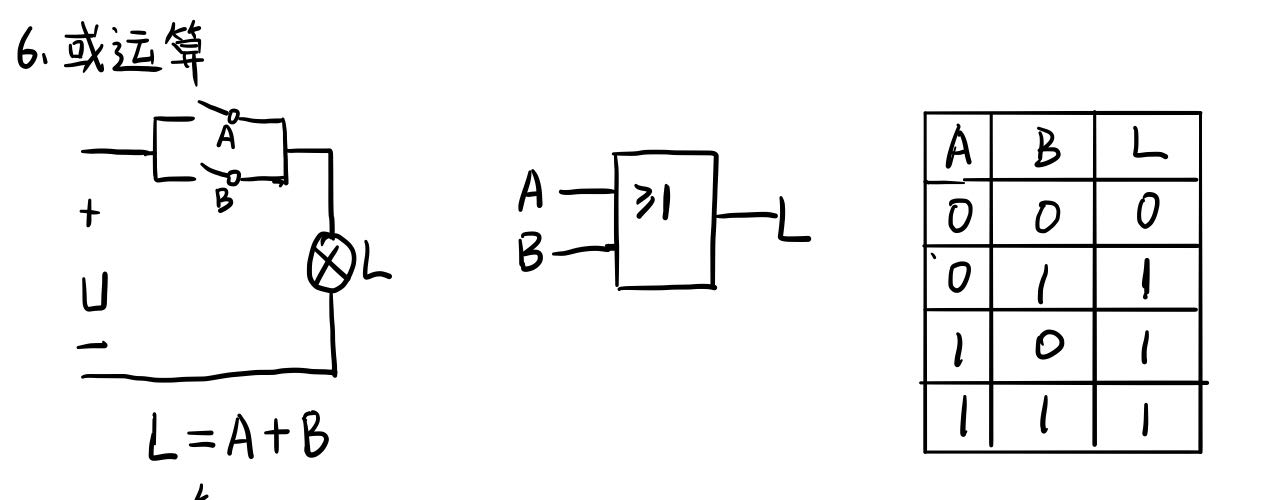
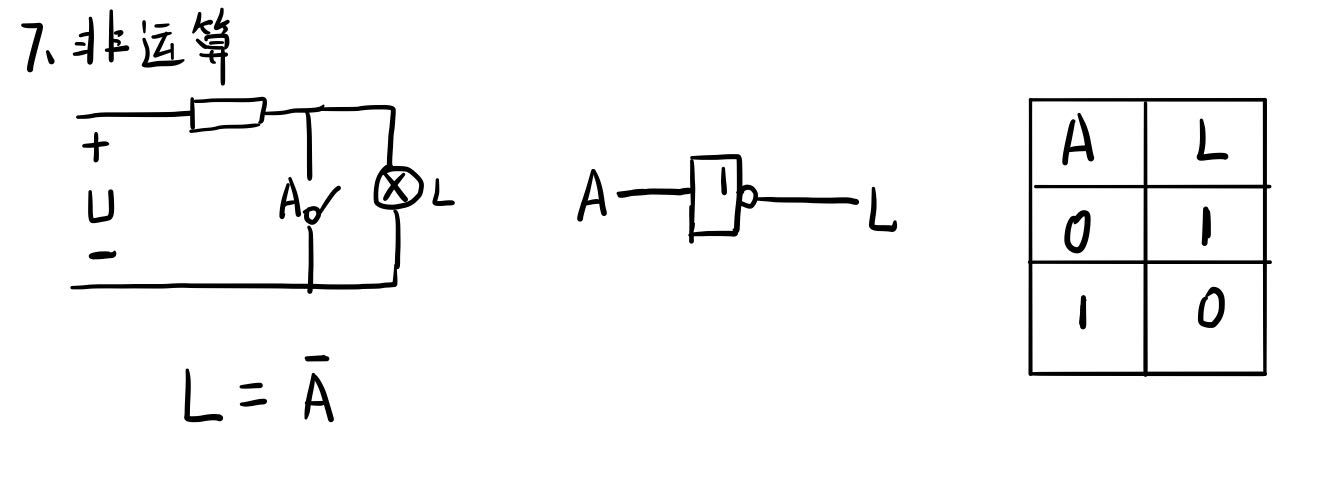
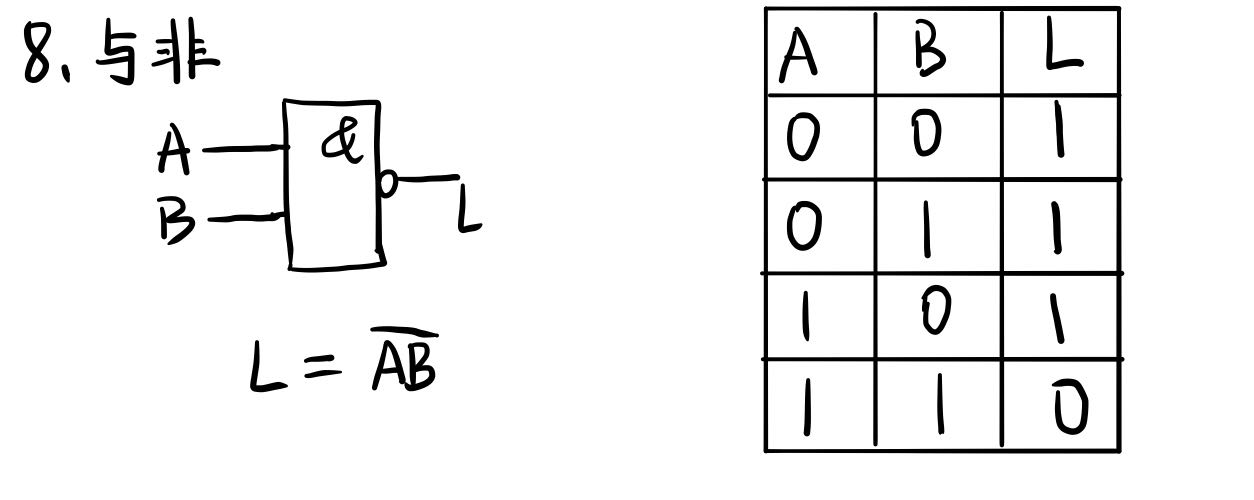
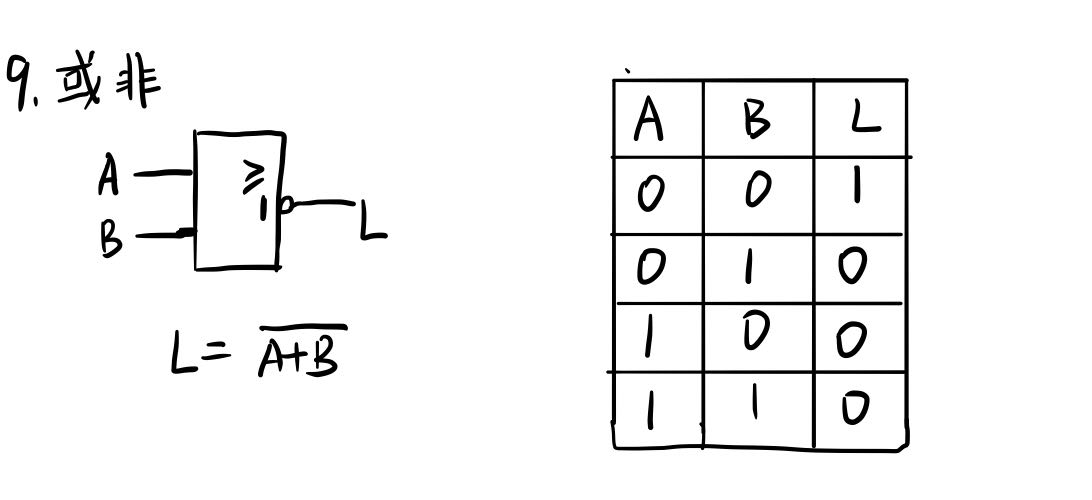

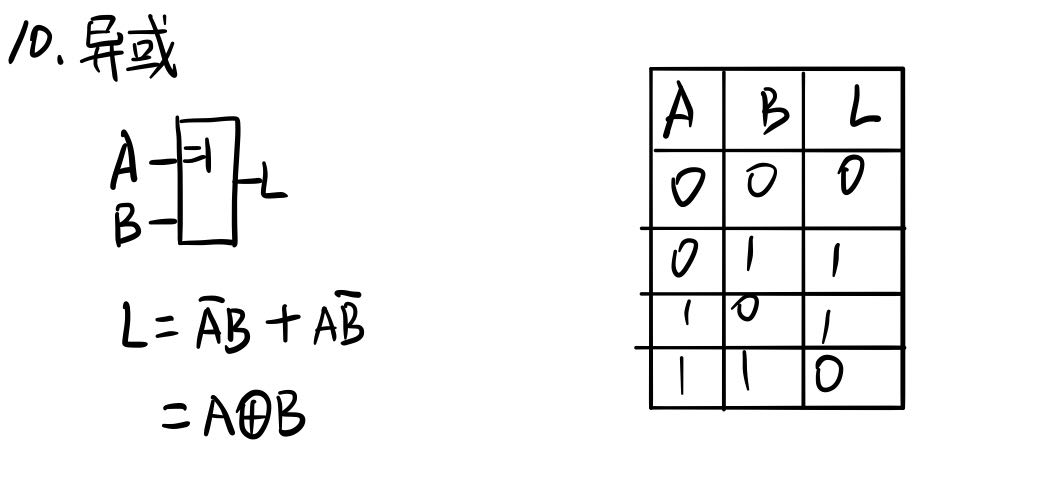
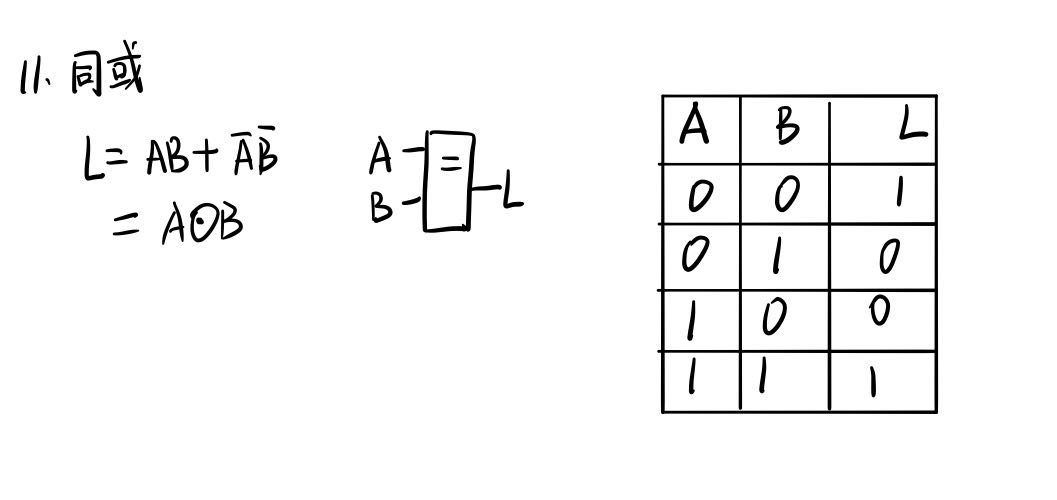
最后
以上就是虚幻蜗牛最近收集整理的关于数字逻辑基础数字逻辑基础的全部内容,更多相关数字逻辑基础数字逻辑基础内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复