matlab2014a如何画电机效率云图,maxwell电机转矩扫描与使用MTPA策略绘制效率map图...

1.电机转矩扫描

电机用的ipm_1工具

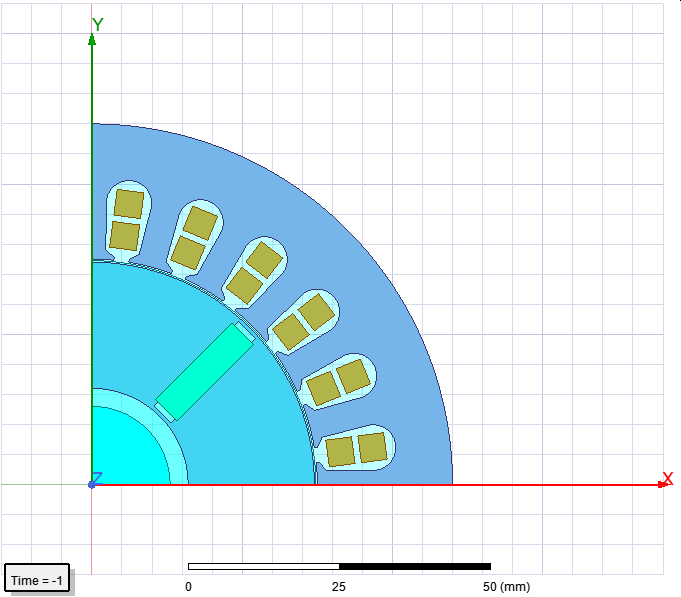
电流激励设置：3d

A相：Im*sin(2*pi*fs*time+th)

B相：Im*sin(2*pi*fs*time+th-2*pi/3)

C相：Im*sin(2*pi*fs*time+th+2*pi/3)

初始机械角度：blog

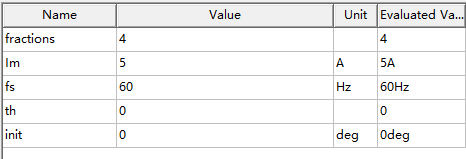
电机参数：(先保持init和th都为0)ip

A相轴线位置：it

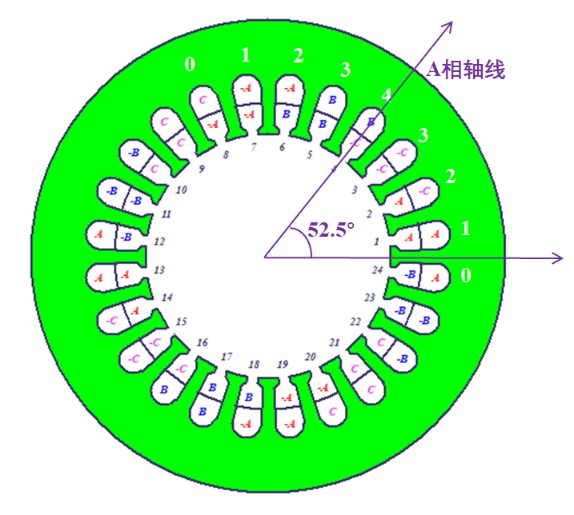
N极轴线：io

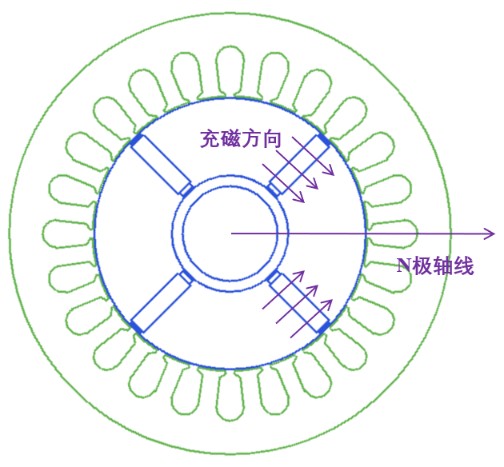
1.1初始机械角度

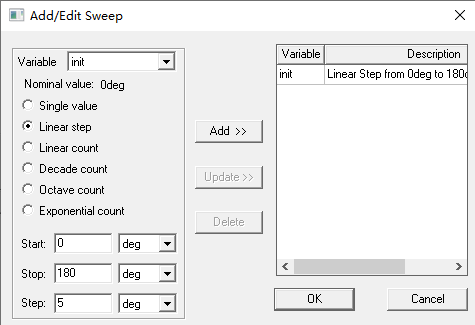
首先扫描init(原始设置是52.5deg)，因为电机有两对极，因此扫描范围是0到180度，间隔5度。table

观察转矩图：class

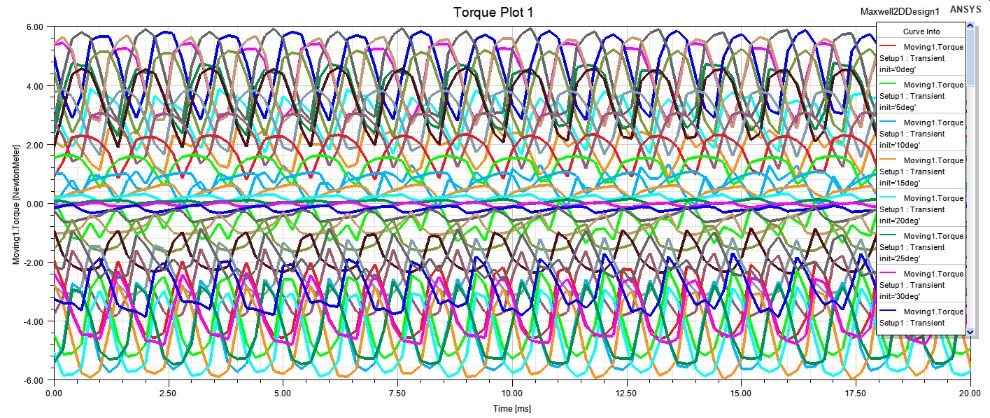
能够看到，不一样init下转矩有明显变化。下面以init为横轴，平均转矩为纵轴，进行进一步观察。效率

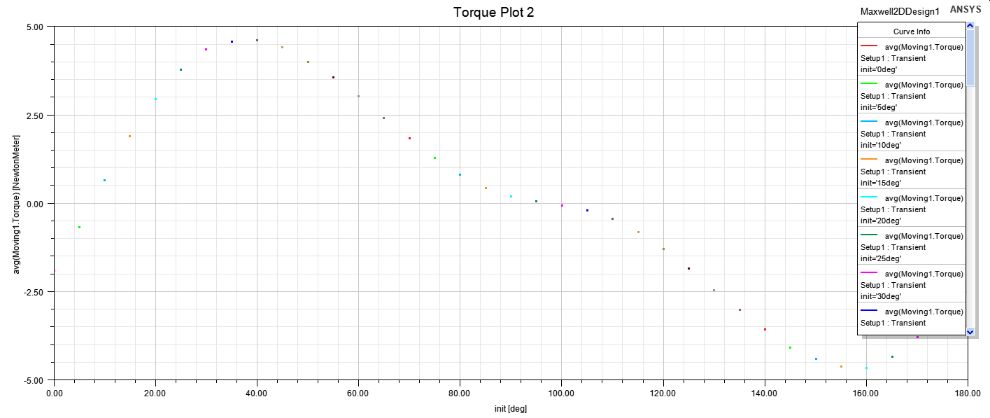
能够看到，在5~95deg区间内转矩为正，电机工做在电动状态，其余区间转矩为负，电机工做在发电状态。40deg时电机转矩达到最大值。csv

在35~45deg进行进一步扫描，以下图。

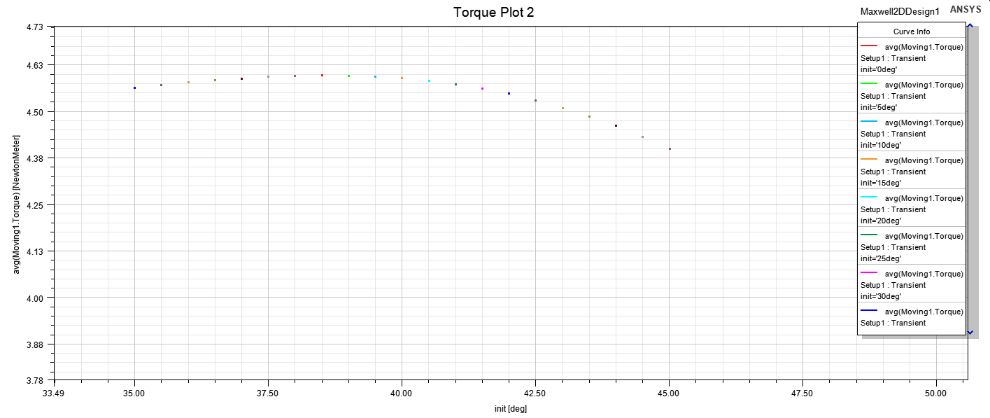
init为38.5deg时，转矩达到最大，为4.5956Nm。

1.2电流角

对th进行扫描。

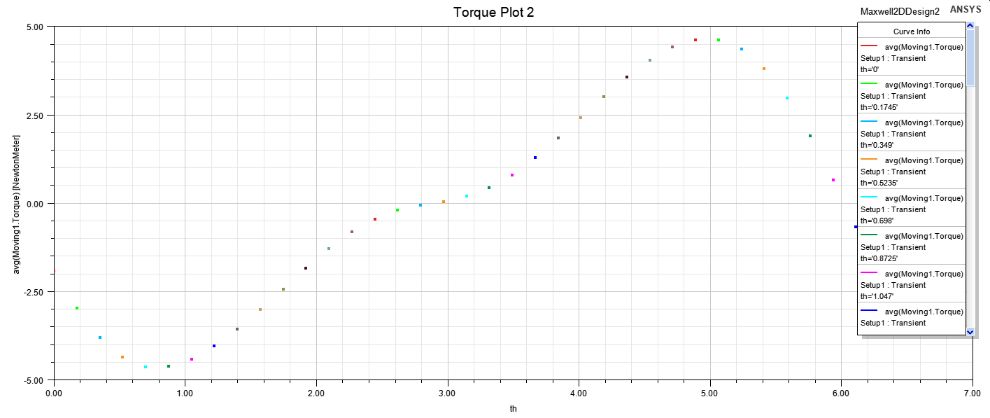
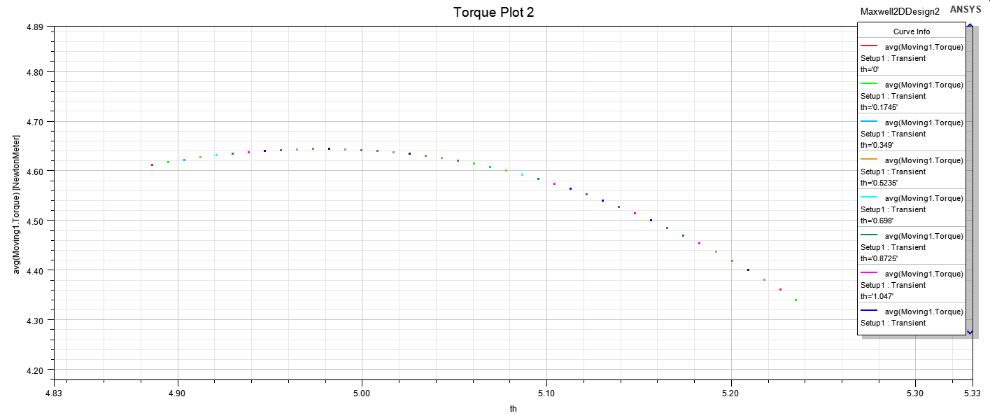
th为4.97327(285度)时转矩最大，最大值为4.643Nm。

1.3小结

能够看到，上面的两幅图有轴对称关系，即设置init和设置th是等价的，当th为285度时，即再通过75度电角度才到达零点，也能够说成让转子先转约38度机械角度。略小于52.5度，及定子磁场超前于转子磁场。

画出下图，能更好地说明这一问题。

data1

data2

plot(data1$init..deg.,data1$avg.Moving1.Torque...deg.,type="l",col="red")

par(new=TRUE)

plot((2*pi-data2$th...)/pi*90,data2$avg.Moving1.Torque....,type="l",col="blue")

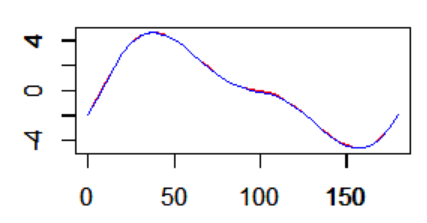
能够看到，两者几乎彻底重合。

若是开启机械瞬态分析，则能够看到转速的波动，但此时没有添加外电路，因此不能设定控制策略。

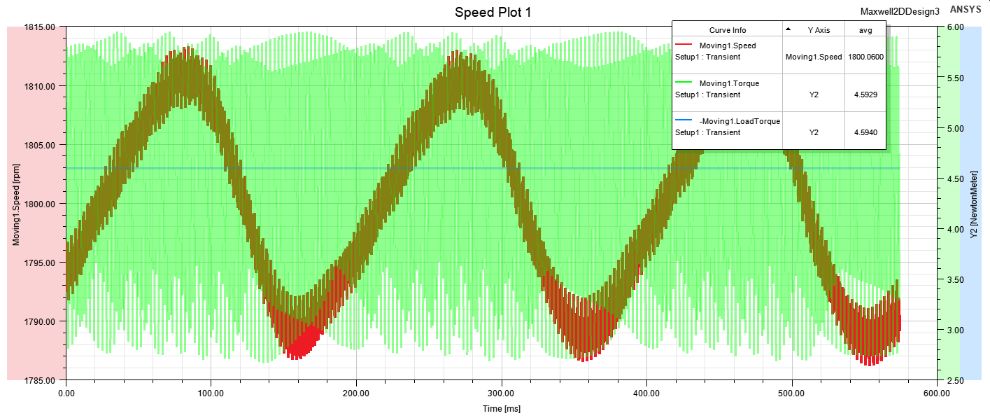
2.MTPA

2.1dq变换

下面对不一样的电流进行扫描，在此以前先回顾一下Clark和Park变换，即Id和Iq的计算。

以前在matlab中搭建的模型：

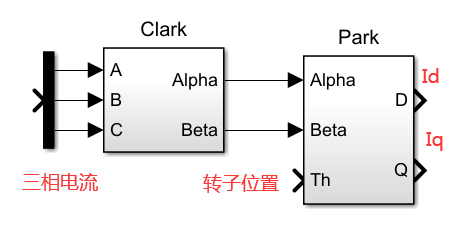
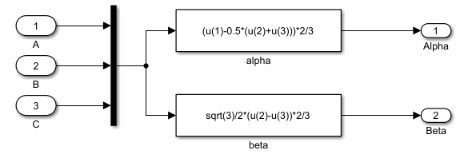
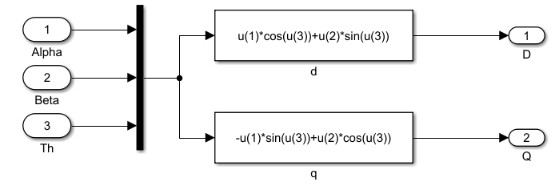
即

[I_d=I_alphacos(th)+I_betasin(th)\=frac{2}{3}(I_a-0.5(I_b+I_c))cos(th)+frac{2}{3}frac{sqrt3}{2}(I_b-I_c)sin(th)\=frac{2}{3}(I_acos(th)+I_bcos(th-frac{2pi}{3})+I_ccos(th+frac{2pi}{3}))]

同理

[I_q=-I_alphasin(th)+I_betacos(th)\=-frac{2}{3}(I_a-0.5(I_b+I_c))sin(th)+frac{2}{3}frac{sqrt3}{2}(I_b-I_c)cos(th)\=-frac{2}{3}(I_asin(th)+I_bsin(th-frac{2pi}{3})+I_csin(th+frac{2pi}{3}))]

在maxwell的Output Variables中能够进行这样的设置：

2.2MTPA

保持init=52.5deg，即d轴和A相轴线对齐，扫描Im和th，其中th扫描范围0~2*pi，步长0.1745(10deg)，Im扫描范围0~7.5A，步长0.5A。

获得下图：

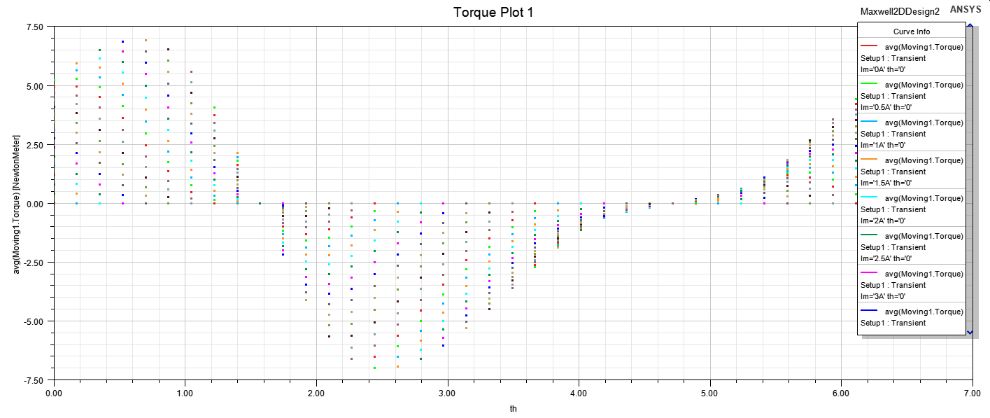
导出表格

获得下表：

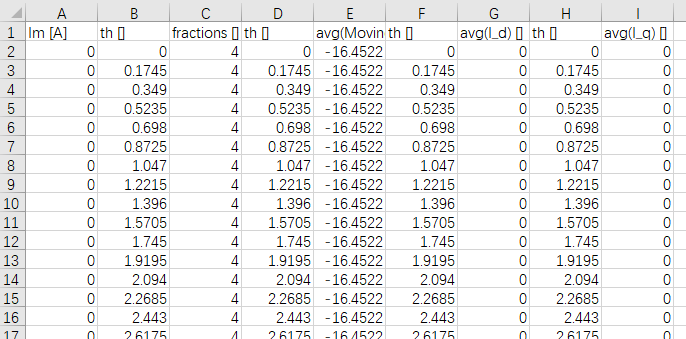
绘图观察一下：

data

data

library(ggplot2)

ggplot(data,aes(th...,avg.Moving1.Torque....,col=factor(Im..A.)))+geom_line()

ggplot(data,aes(th...,avg.Moving1.Torque....,col=factor(Im..A.)))+geom_line()+

xlim(0,1.7)+ylim(-1000,7000)

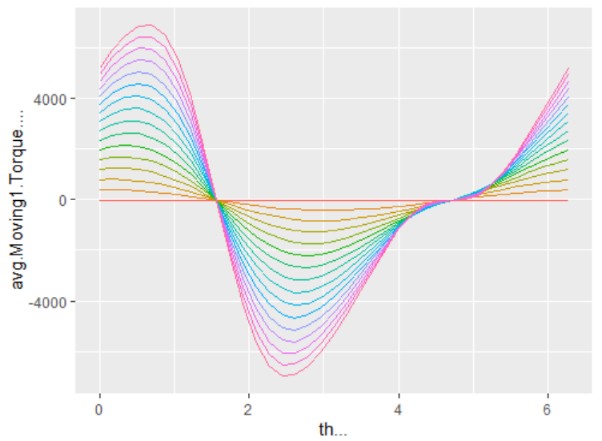
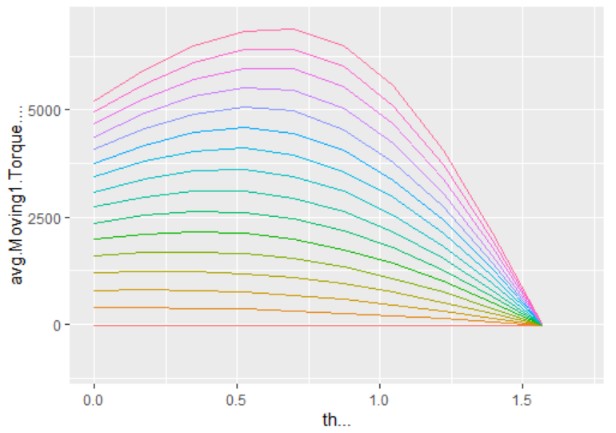
寻找每一个电流下的最大转矩：

I

n

temp

table

for(i in 1:n){

dataI

index

table[i,]

}

获得表格：

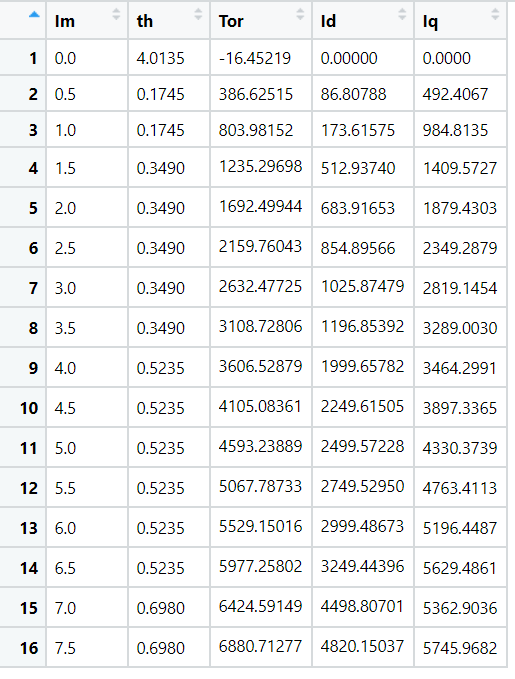
这就是这一转速下的转矩指令表。

2.3效率MAP

下面利用maxwell中的工具绘制效率map，与上面的扫描结果进行对比。

在View菜单栏中打开ACT Extensions工具。

选择Machine Toolkit进入。

选择待求解的工程，并进行相应设置。

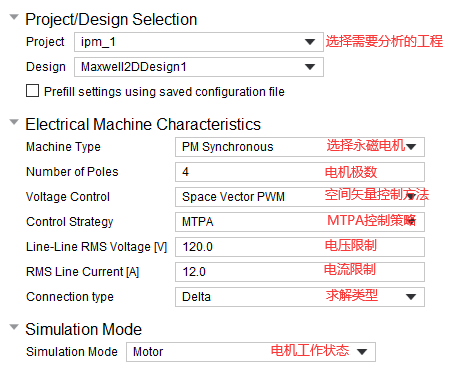
其中极数是为了肯定电流频率和电机转速的关系。

设置求解精度。

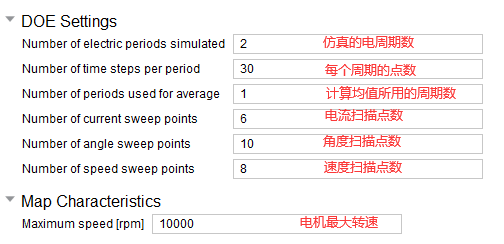
进一步设置：(通常保持默认便可)

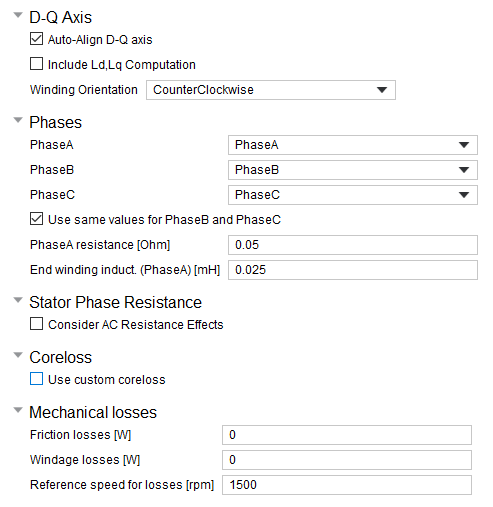
完成设置后点击Finish开始计算。

计算完成后获得下列图像。

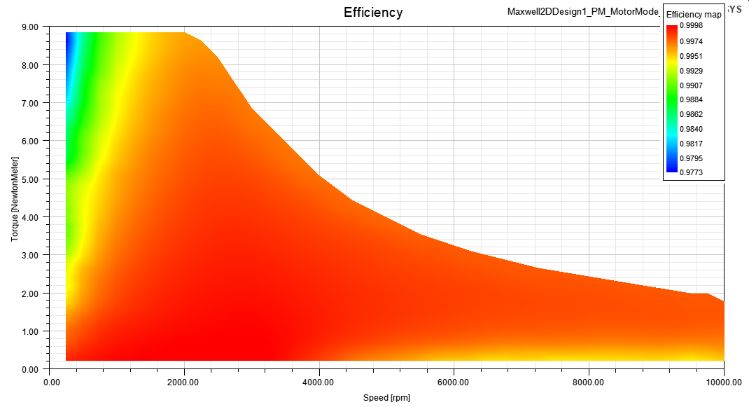
由于损耗中只考虑了StrandedLoss，因此效率很高。

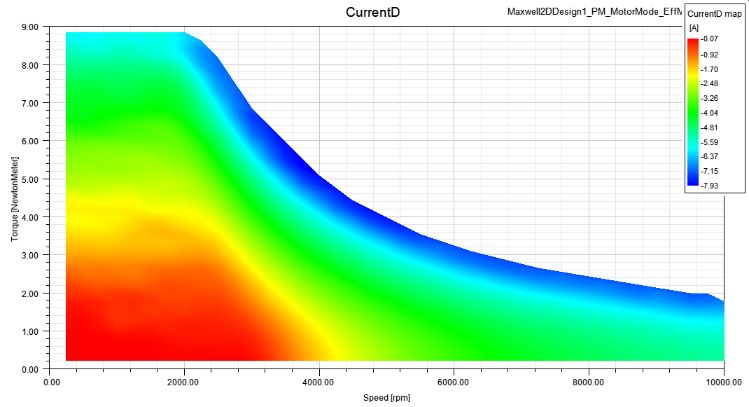
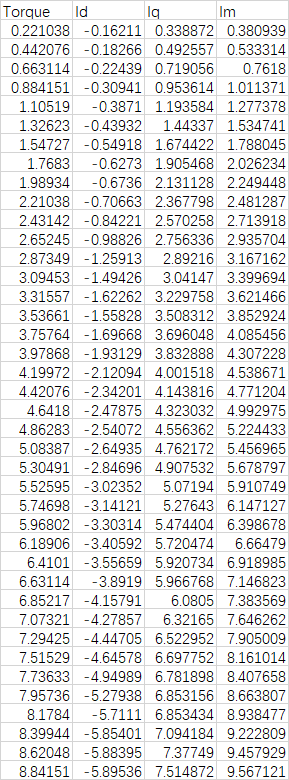
ID：

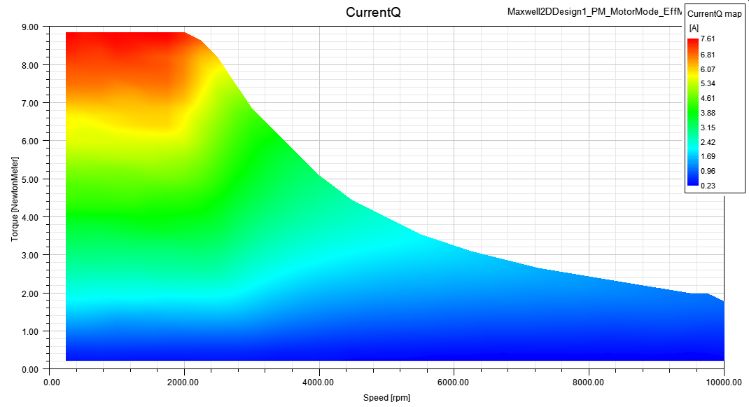
IQ：

Im/1.414=Irms：

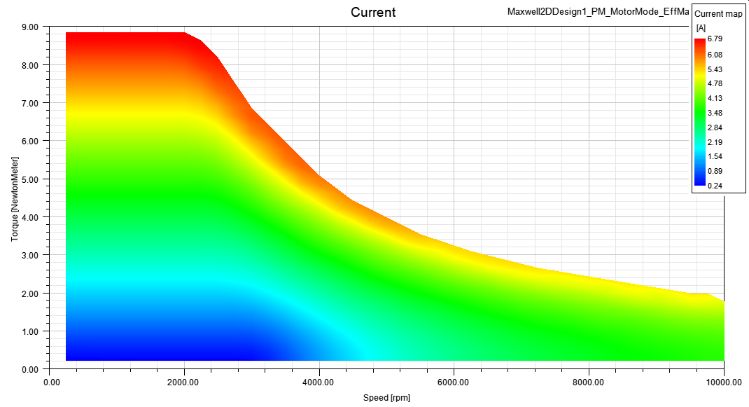
提取转速为1800rpm处的值：

并与扫描法获得的结果对比，以下图：

library(readxl)

table2

layout(matrix(c(1,1,2,3), 2, 2, byrow = FALSE),

widths=c(1, 1), heights=c(1, 1))

plot(table$Tor,table$Im,type="l",col="red",xlim=c(0,7000),ylim=c(0,8),xlab="Torque/mNm",ylab="Im/A")

par(new=TRUE)

plot(1000*table2$Torque,table2$Im,type="l",col="blue",xlim=c(0,7000),ylim=c(0,8),xlab="",ylab="")

legend("topleft",legend=c("sweep","toolkit"),

col=c("red","blue"),lty=1,lwd=2)

plot(table$Tor,-table$Id,type="l",col="red",xlim=c(0,7000),ylim=c(-5000,0),xlab="Torque/mNm",ylab="Id/mA")

par(new=TRUE)

plot(1000*table2$Torque,1000*table2$Id,type="l",col="blue",xlim=c(0,7000),ylim=c(-5000,0),xlab="",ylab="")

legend("bottomleft",legend=c("sweep","toolkit"),

col=c("red","blue"),lty=1,lwd=2)

plot(table$Tor,table$Iq,type="l",col="red",xlim=c(0,7000),ylim=c(0,6000),xlab="Torque/mNm",ylab="Iq/mA")

par(new=TRUE)

plot(1000*table2$Torque,1000*table2$Iq,type="l",col="blue",xlim=c(0,7000),ylim=c(0,6000),xlab="",ylab="")

legend("topleft",legend=c("sweep","toolkit"),

col=c("red","blue"),lty=1,lwd=2)

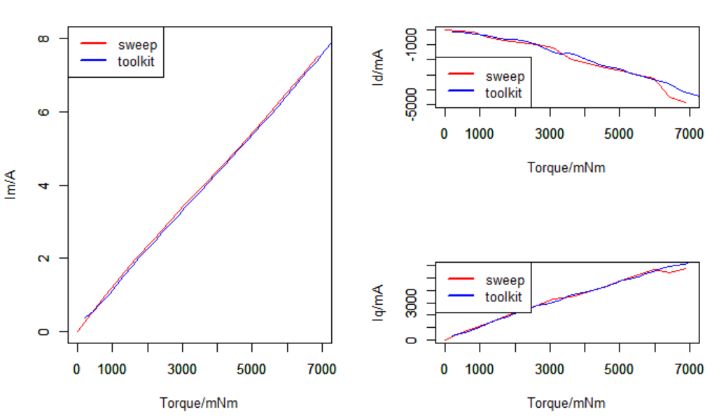
可见两者很是接近，从方法上说是一致的。也就是说，使用扫描法多考虑几个转速取值，并兼顾电流和电压限制，一样能够手动绘出效率map图。