umap入门定义实现使用 umap 用于聚类

定义

 该算法基于关于数据的三个假设：

• 数据均匀分布在黎曼流形上（Riemannian manifold）；
• 黎曼度量是局部恒定的（或可以这样近似）；
• 流形是局部连接的。

一种降维技术，假设可用数据样本均匀（Uniform）分布在拓扑空间（Manifold）中，可以从这些有限数据样本中近似（Approximation）并映射（Projection）到低维空间。

实现

1. 学习高维空间中的流形结构

1.1 寻找最近的邻居

nearest-neighbor-descent算法找邻居

n_neighbors 参数指定想要的近邻点数量【要进行不断验证---控制这数据的局部和全局结构】

1.2 构建图

UMAP通过连接来确定最近邻来构建图，图的形成过程分为

1.2.1 变化距离

假设在流形上均匀分布，表明空间根据数据看起来稀疏/密集的位置拉伸和收缩的

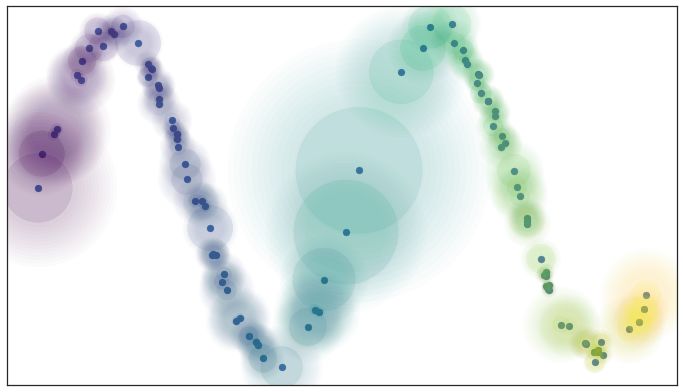
它本质上意味着距离度量不是在整个空间中通用的，而是在不同区域之间变化的。我们可以通过在每个数据点周围绘制圆圈/球体来对其进行可视化，由于距离度量的不同，它们的大小似乎不同

1.2.2 local_connectivity

接下来，我们要确保试图学习的流形结构不会导致许多不连通点。所以需要使用另一个超参数local_connectivity(默认值= 1)来解决这个潜在的问题

当我们设置local_connectivity=1 时，我们告诉高维空间中的每一个点都与另一个点相关联。

1.2.3 模糊区域

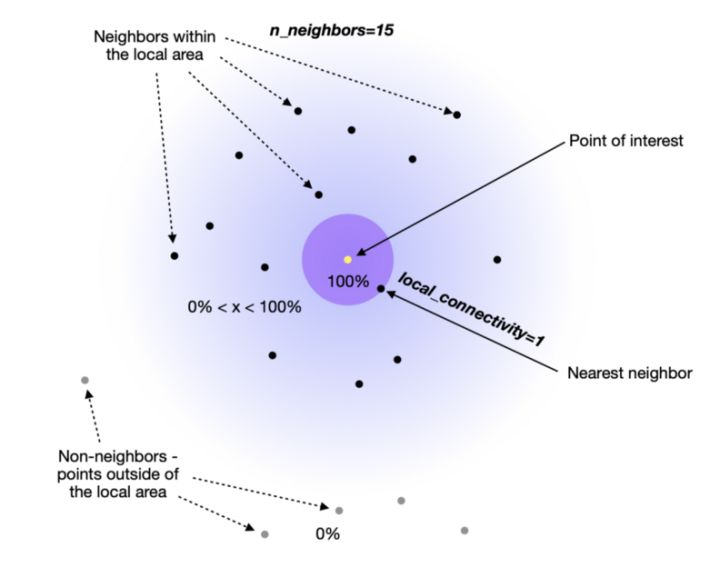
你一定已经注意到上面的图也包含了模糊的圆圈延伸到最近的邻居之外。这告诉我们，当我们离感兴趣的点越远，与其他点联系的确定性就越小。

这两个超参数（local_connectivity 和 n_neighbors）最简单的理解就是可以将他们视为下限和上限：

Local_connectivity(默认值为1)：100%确定每个点至少连接到另一个点(连接数量的下限)。

n_neighbors(默认值为15)：一个点直接连接到第 16 个以上的邻居的可能性为 0%，因为它在构建图时落在 UMAP 使用的局部区域之外。

2 到 15 ： 有一定程度的确定性（>0% 但 <100%）一个点连接到它的第 2 个到第 15 个邻居。

1.2.4 边的合并

连接确定性是通过边权重（w）来表达的。由于我们采用了不同距离的方法，因此从每个点的角度来看，我们不可避免地会遇到边缘权重不对齐的情况。 例如，点 A→B 的边权重与 B→A 的边权重不同。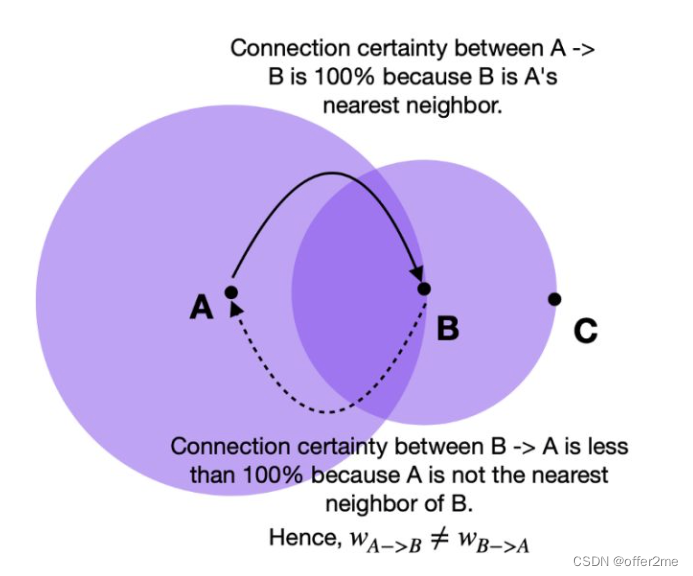

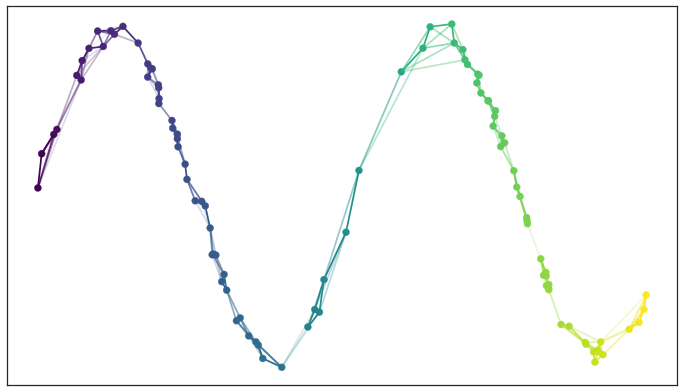
 如果我们想将权重为 a 和 b 的两条不同的边合并在一起，那么我们应该有一个权重为 + − ⋅ 的单边。 考虑这一点的方法是，权重实际上是边（1-simplex）存在的概率。 组合权重就是至少存在一条边的概率。

2. 找到该流形的低维表示

从高维空间学习近似流形后，UMAP 的下一步是将其投影（映射）到低维空间。

2.1.最小距离

与第一步不同，我们不希望在低维空间表示中改变距离。相反，我们希望流形上的距离是相对于全局坐标系的标准欧几里得距离。

从可变距离到标准距离的转换的转换也会影响与最近邻居的距离。因此，我们必须传递另一个名为 min_dist（默认值=0.1）的超参数来定义嵌入点之间的最小距离。

本质上，我们可以控制点的最小分布，避免在低维嵌入中许多点相互重叠的情况。

2.2.最小化成本函数（Cross-Entropy）

指定最小距离后，该算法可以开始寻找较好的低维流形表示。 UMAP 通过最小化以下成本函数（也称为交叉熵 (CE)）来实现：

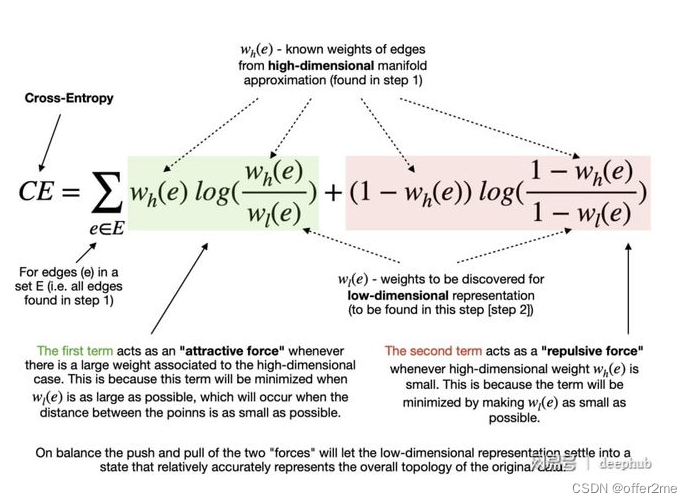
最终目标是在低维表示中找到边的最优权值。这些最优权值随着上述交叉熵函数的最小化而出现，这个过程是可以通过随机梯度下降法来进行优化的

使用

1. 超参数

• n_neighbor---- 平衡 local versus global structure 

它控制 UMAP 在构建流形时为每个样本查看的本地邻域的区域。较小的值将关注点缩小到局部结构，考虑到特性和小模式，可能会失去全局。

较高的值可n_neighbors提供更大的灵活性，并允许 UMAP 专注于相应维度中数据的更广泛“视图”。当然，这是以丢失结构的细节为代价的。此参数的默认值为 15。

• min_dist

另一个关键参数是min_dist控制数据点之间的字面距离。您可以调整默认值 0.1 以控制不同点云的紧密度。较低的值将导致嵌入更密集，可更轻松地查看单个集群。这在聚类期间可能很有用。相比之下，接近 1 的值会给点更多的喘息空间，让您能够看到更广泛的拓扑结构。

• n_components

控制想要压缩的维度，默认设置为2；

对于超过100个特征的数据集，2D不能完全保留数据拓扑结构，5步尝试2-20之间的值，并评估不同基线模型 查看准确性的变化

• metric

metric表示计算点之间距离的公式。默认值为euclidean，但您可以在许多其他选项中进行选择，manhattan包括minkowski和chebyshev。

 fit = umap.UMAP(
        n_neighbors=n_neighbors,
        min_dist=min_dist,
        n_components=n_components,
        metric=metric
    )
    u = fit.fit_transform(data);

 umap 用于聚类

利用 UMAP 执行非线性流形感知降维，可以将数据集降低到足够小的维度，以便基于密度的聚类算法取得进展。UMAP 的一个优点是它不需要您只减少到两个维度 - 您可以减少到 10 个维度，因为目标是聚类，而不是可视化，并且 UMAP 的性能成本最小。碰巧 MNIST 是一个非常简单的数据集，我们真的可以将它一直推到只有两个维度，但通常你应该探索不同的嵌入维度选项。

接下来要注意的是，当使用 UMAP 进行降维时，您将需要选择与使用 UMAP 进行可视化不同的参数。首先，我们需要一个较大的 n_neighbors值——较小的值将更多地关注非常局部的结构，并且更容易产生细粒度的集群结构，这可能是数据中噪声模式的结果，而不是实际类别。在这种情况下，我们会将其从默认的 15 加倍到 30。

其次，将其设置min_dist为非常低的值是有益的。由于我们实际上希望将点密集地打包在一起（毕竟密度是我们想要的），因此较低的值会有所帮助，并且可以在集群之间进行更清晰的分离。在这种情况下，我们将简单地设置 min_dist为 0。

最后

以上就是明理店员为你收集整理的umap入门定义实现使用 umap 用于聚类的全部内容，希望文章能够帮你解决umap入门定义实现使用 umap 用于聚类所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。