简介
误差反向传播算法简称反向传播算法(即BP算法)。
使用反向传播算法的多层感知器又称为BP神经网络。BP算法是一个迭代算法,它的基本思想为:
-
1、先计算每一层的状态和激活值,直到最后一层(前向传播)
-
2、计算每一层的误差,误差的计算过程是从最后一层向前推进的
-
3、更新参数(目标是误差变小)。迭代前面两个步骤,直到满足停止准则(比如相邻两次迭代的误差的差别很小)
本文约定
对于M-P神经元和感知机(简单的前馈神经网络)都在上一篇博文中介绍了,现在先规定一下下面讲解推到过程的时候的一些记号
-
n l n_l nl表示第 l l l层的神经元个数
-
f ( ⋅ ) f(·) f(⋅) 表示神经元的激活函数(激活函数我另外会再开一篇博文来记录)
-
W ( l ) ∈ R n l × n l W^{(l)} in mathbb{R}^{n_l times n_l} W(l)∈Rnl×nl 表示第 l − 1 l-1 l−1 层到第 l l l 层的权重矩阵
-
w i j ( l ) w^{(l)}_{ij} wij(l)表示第 l l l层的第 j j j个神经元与上一个,即 ( l − 1 ) (l-1) (l−1)层的第 i i i个神经元的连接权重
-
b i ( l ) b^{(l)}_i bi(l)表示第 l l l层的第 i i i个神经元的偏置
-
b ( l ) = ( b 1 ( l ) , b 2 ( l ) , . . . , b n l ( l ) ) T ∈ R l n b^{(l)} = (b^{(l)}_1, b^{(l)}_2,...,b^{(l)}_{n_l})^Tinmathbb{R}^n_l b(l)=(b1(l),b2(l),...,bnl(l))T∈Rln表示第 l − 1 l-1 l−1层到第 l l l层的偏置
-
z i ( l ) z^{(l)}_i zi(l) 表示第 l l l层中第 i i i个神经元节点的输入值
-
z ( l ) = ( z 1 ( l ) , z 2 ( l ) , . . . , z n l ( l ) ) T ∈ R l n z^{(l)} = (z^{(l)}_1, z^{(l)}_2,...,z^{(l)}_{n_l})^Tinmathbb{R}^n_l z(l)=(z1(l),z2(l),...,znl(l))T∈Rln表示第 l − 1 l-1 l−1层到第 l l l层的输入
-
a i ( l ) a^{(l)}_i ai(l)表示第 l l l层中第 i i i个神经元节点的激活值(输出值)
使用的图片来源网络,部分符号约定不同自行变通
本文以三层感知机为例
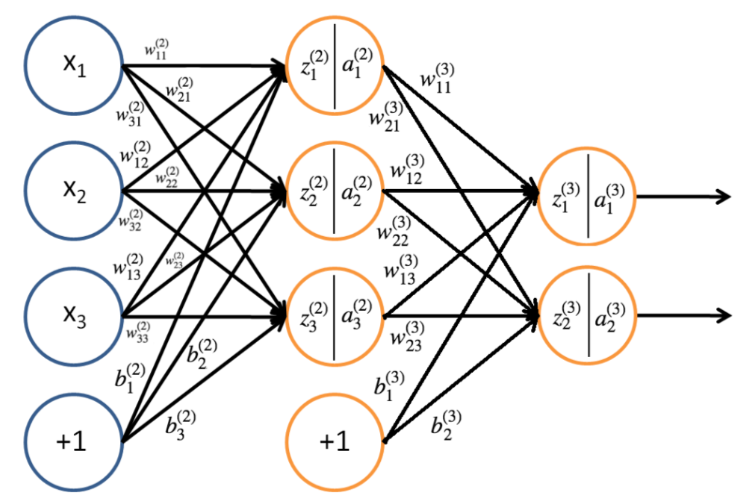
信息前向传播
由该神经网络可以得出第二层的参数
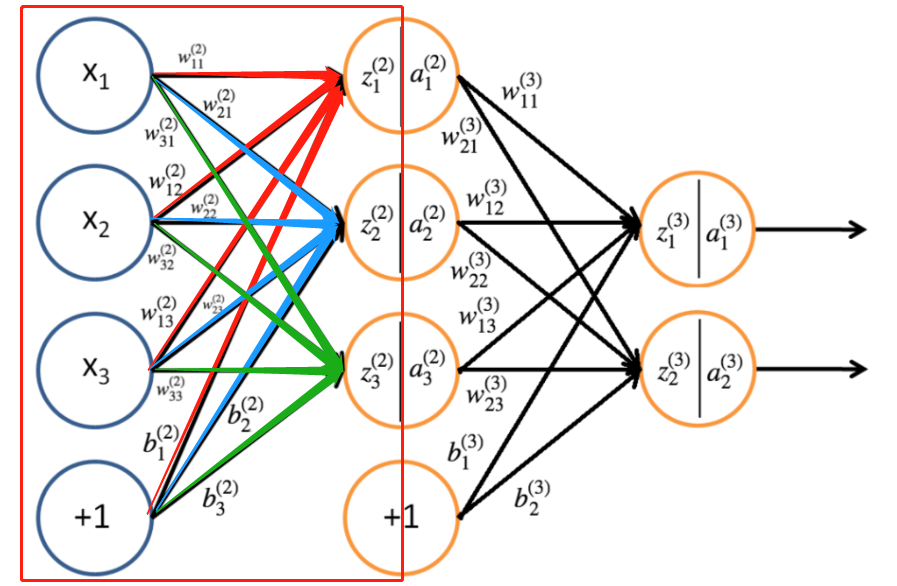
并且,我们能够用相同的方法计算第三层的参数
所以可以总结出,第
l
(
2
≤
l
≤
L
)
l(2leq l leq L)
l(2≤l≤L) 层神经元的输入和激活值(输出值)
所以对于前馈神经网络的信息前向传播的传递过程入下:
误差反向传播
目的:调整 w 、 b w 、 b w、b权重和偏置直到最优,知道损失函数最小为止
使用方法:梯度下降法(本文使用批量梯度下降、随机梯度下降)
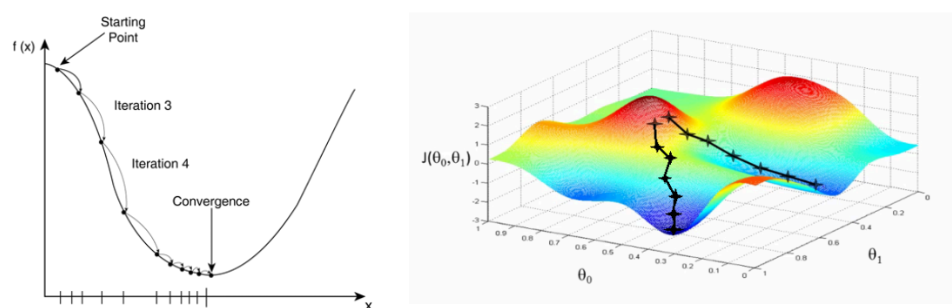
权重和偏置的更新规则为:
-
w n e w 、 w o l d w_{new}、w_{old} wnew、wold 表示该连接的新权重和旧的权重
-
b n e w 、 b o l d b_{new}、b_{old} bnew、bold 表示该连接的新偏置和旧的偏置
-
J t o t a l J_{total} Jtotal表示每个 ( x ( i ) , y ( i ) ) (x_{(i)},y_{(i)}) (x(i),y(i)) 数据计算出的损失函数的平均
μ mu μ 代表学习率,即“步长”
下面我们求损失函数(本文使用平均损失,交叉熵损失函数暂无)
对于训练数据为 ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , . . . , ( x ( N ) , y ( N ) ) {(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(N)},y^{(N)})} (x(1),y(1)),(x(2),y(2)),...,(x(N),y(N))即总共由 N N N组训练数据(不含测试数据),所以它最后的输出的训练实际值就有 y ( i ) = ( y 1 ( i ) , ⋅ ⋅ ⋅ , y n L ( i ) ) T y^{(i)} = (y^{(i)}_1,···,y^{(i)}_{nL})^T y(i)=(y1(i),⋅⋅⋅,ynL(i))T
对于某一个数训练数据 ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i))来说就有一个损失函数:
-
y ( i ) y^{(i)} y(i)代表期望的输出,也就是我们自己给出的数据中的 y y y值
-
o ( i ) o^{(i)} o(i) 为网络的实际输出
所以一个epoch下来,的平均损失:
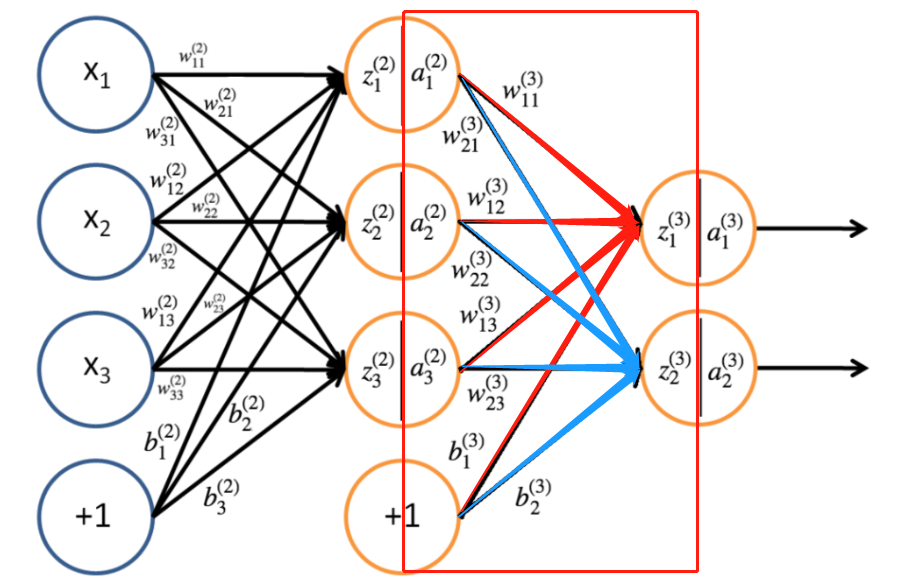
输出层权重更新
还是用本文前那个神经网络进行示例进行输出层权重的更新
$ J_{(3)} = frac{1}{2}parallel y{(3)}-o{(3)}parallel qquad = frac{1}{2}parallel y{(3)}-a{(3)}parallel qquad =frac{1}{2}left [(y{(3)}_1-a{(3)}_1)2+(y{(3)}_2-a{(3)}_1)2 right ] qquad =frac{1}{2}left {left [y{(3)}_1-f(z{(3)}_1)right]^2+left [y{(3)}_2-f(z{(3)}2)right]^2right } qquad =frac{1}{2}left {left [y{(3)}_1-f(w{3}{11}a^{(2)}_1 + w{3}_{21}a{(2)}_2 + w{3}_{31}a{(2)}3 + b{(3)}_1)right]2+left [y{(3)}_2-f(w{3}{12}a^{(2)}_1 + w{3}_{22}a{(2)}_2 + w{3}_{32}a{(2)}_3 + b{(3)}_2)right]2right } $
由链式求导法则去分别对 w 11 ( 3 ) 、 w 21 ( 3 ) 、 w 31 ( 3 ) w^{(3)}_{11}、w^{(3)}_{21}、w^{(3)}_{31} w11(3)、w21(3)、w31(3)求偏导
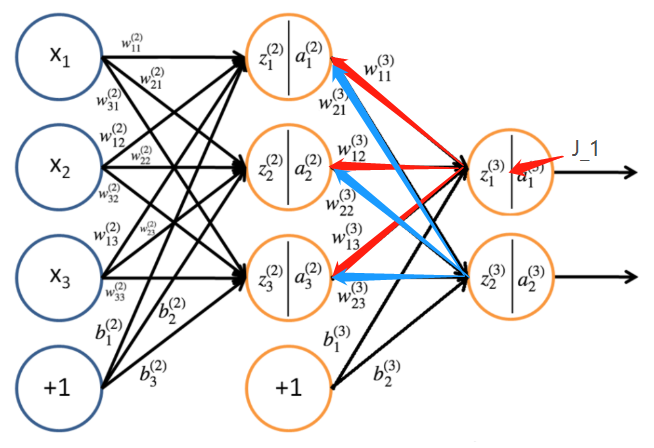
∂
J
3
∂
w
11
(
3
)
=
∂
J
3
∂
a
1
(
3
)
∂
a
1
(
3
)
∂
z
1
(
3
)
∂
z
1
(
3
)
∂
w
11
(
3
)
frac{partial J_3}{partial w^{(3)}_{11}}=frac{partial J_{3}}{partial a^{(3)}_1}frac{partial a^{(3)}_1}{partial z^{(3)}_1}frac{partial z^{(3)}_1}{partial w^{(3)}_{11}}
∂w11(3)∂J3=∂a1(3)∂J3∂z1(3)∂a1(3)∂w11(3)∂z1(3)
∂
J
3
∂
w
21
(
3
)
=
∂
J
3
∂
a
1
(
3
)
∂
a
1
(
3
)
∂
z
1
(
3
)
∂
z
1
(
3
)
∂
w
21
(
3
)
frac{partial J_3}{partial w^{(3)}_{21}}=frac{partial J_{3}}{partial a^{(3)}_1}frac{partial a^{(3)}_1}{partial z^{(3)}_1}frac{partial z^{(3)}_1}{partial w^{(3)}_{21}}
∂w21(3)∂J3=∂a1(3)∂J3∂z1(3)∂a1(3)∂w21(3)∂z1(3)
∂
J
3
∂
w
31
(
3
)
=
∂
J
3
∂
a
1
(
3
)
∂
a
1
(
3
)
∂
z
1
(
3
)
∂
z
1
(
3
)
∂
w
31
(
3
)
frac{partial J_3}{partial w^{(3)}_{31}}=frac{partial J_{3}}{partial a^{(3)}_1}frac{partial a^{(3)}_1}{partial z^{(3)}_1}frac{partial z^{(3)}_1}{partial w^{(3)}_{31}}
∂w31(3)∂J3=∂a1(3)∂J3∂z1(3)∂a1(3)∂w31(3)∂z1(3)
∂
J
3
∂
w
12
(
3
)
=
∂
J
3
∂
a
2
(
3
)
∂
a
2
(
3
)
∂
z
2
(
3
)
∂
z
1
(
3
)
∂
w
12
(
3
)
frac{partial J_3}{partial w^{(3)}_{12}}=frac{partial J_{3}}{partial a^{(3)}_2}frac{partial a^{(3)}_2}{partial z^{(3)}_2}frac{partial z^{(3)}_1}{partial w^{(3)}_{12}}
∂w12(3)∂J3=∂a2(3)∂J3∂z2(3)∂a2(3)∂w12(3)∂z1(3)
∂
J
3
∂
w
22
(
3
)
=
∂
J
3
∂
a
2
(
3
)
∂
a
2
(
3
)
∂
z
2
(
3
)
∂
z
1
(
3
)
∂
w
22
(
3
)
frac{partial J_3}{partial w^{(3)}_{22}}=frac{partial J_{3}}{partial a^{(3)}_2}frac{partial a^{(3)}_2}{partial z^{(3)}_2}frac{partial z^{(3)}_1}{partial w^{(3)}_{22}}
∂w22(3)∂J3=∂a2(3)∂J3∂z2(3)∂a2(3)∂w22(3)∂z1(3)
∂
J
3
∂
w
32
(
3
)
=
∂
J
3
∂
a
2
(
3
)
∂
a
2
(
3
)
∂
z
2
(
3
)
∂
z
1
(
3
)
∂
w
32
(
3
)
frac{partial J_3}{partial w^{(3)}_{32}}=frac{partial J_{3}}{partial a^{(3)}_2}frac{partial a^{(3)}_2}{partial z^{(3)}_2}frac{partial z^{(3)}_1}{partial w^{(3)}_{32}}
∂w32(3)∂J3=∂a2(3)∂J3∂z2(3)∂a2(3)∂w32(3)∂z1(3)
再拿 w 11 ( 3 ) w^{(3)}_{11} w11(3)为例,带入求偏导得:
∂ J 3 ∂ w 11 ( 3 ) = 1 2 ⋅ 2 ( y 1 ( 3 ) − a 1 ( 3 ) ) ( − ∂ a 1 ( 3 ) ∂ w 11 ( 3 ) ) = − ( y 1 ( 3 ) − a 1 ( 3 ) ) f ′ ( z 1 ( 3 ) ) ∂ z 1 ( 3 ) ∂ w 11 ( 3 ) = − ( y 1 ( 3 ) − a 1 ( 3 ) ) f ′ ( z 1 ( 3 ) ) a 1 ( 2 ) frac{partial J_3}{partial w^{(3)}_{11}}=frac{1}{2}cdot 2(y^{(3)}_1-a^{(3)}_1)(-frac{partial a^{(3)}_1}{partial w^{(3)}_{11}}) \ qquad quad = -(y^{(3)}_1-a^{(3)}_1) f'(z^{(3)}_1)frac{partial z^{(3)}_1}{partial w^{(3)}_{11}} \ qquad = -(y^{(3)}_1-a^{(3)}_1)f'(z^{(3)}_1)a^{(2)}_1 ∂w11(3)∂J3=21⋅2(y1(3)−a1(3))(−∂w11(3)∂a1(3))=−(y1(3)−a1(3))f′(z1(3))∂w11(3)∂z1(3)=−(y1(3)−a1(3))f′(z1(3))a1(2)
根据上面的公式,我们令:
δ i ( l ) = ∂ J ∂ z i ( l ) = ∂ J ∂ a i ( l ) ∂ a i ( l − 1 ) ∂ z i ( l ) = − ( y i ( l ) − a i ( l ) ) f ′ ( z i ( l ) ) delta^{(l)}_i = frac{partial J}{partial z^{(l)}_i}= frac{partial J}{partial a^{(l)}_i}frac{partial a^{(l-1)}_i}{partial z^{(l)}_i} = -(y^{(l)}_i-a^{(l)}_i)f'(z^{(l)}_i) δi(l)=∂zi(l)∂J=∂ai(l)∂J∂zi(l)∂ai(l−1)=−(yi(l)−ai(l))f′(zi(l))
所以:
∂
J
∂
w
11
(
3
)
=
δ
1
(
3
)
a
1
(
2
)
frac{partial J}{partial w^{(3)}_{11}}=delta^{(3)}_1a^{(2)}_1
∂w11(3)∂J=δ1(3)a1(2)
∂
J
∂
w
21
(
3
)
=
δ
1
(
3
)
a
2
(
2
)
frac{partial J}{partial w^{(3)}_{21}}=delta^{(3)}_1a^{(2)}_2
∂w21(3)∂J=δ1(3)a2(2)
∂
J
∂
w
31
(
3
)
=
δ
1
(
3
)
a
3
(
2
)
frac{partial J}{partial w^{(3)}_{31}}=delta^{(3)}_1a^{(2)}_3
∂w31(3)∂J=δ1(3)a3(2)
∂
J
∂
w
12
(
3
)
=
δ
2
(
3
)
a
1
(
2
)
frac{partial J}{partial w^{(3)}_{12}}=delta^{(3)}_2a^{(2)}_1
∂w12(3)∂J=δ2(3)a1(2)
∂
J
∂
w
22
(
3
)
=
δ
2
(
3
)
a
2
(
2
)
frac{partial J}{partial w^{(3)}_{22}}=delta^{(3)}_2a^{(2)}_2
∂w22(3)∂J=δ2(3)a2(2)
∂
J
∂
w
32
(
3
)
=
δ
2
(
3
)
a
3
(
2
)
frac{partial J}{partial w^{(3)}_{32}}=delta^{(3)}_2a^{(2)}_3
∂w32(3)∂J=δ2(3)a3(2)
所以,假设神经网络一共由 L L L层,那么对一般式而言:
δ
i
(
L
)
=
−
(
y
i
(
L
)
−
a
i
(
L
)
)
f
′
(
z
i
(
L
)
)
delta^{(L)}_i = -(y^{(L)}_i-a^{(L)}_i)f'(z^{(L)}_i)
δi(L)=−(yi(L)−ai(L))f′(zi(L))
∂
J
w
i
j
(
L
)
=
δ
i
(
L
)
a
i
(
L
−
1
)
frac{partial J}{w^{(L)}_{ij}} = delta^{(L)}_ia^{(L-1)}_i
wij(L)∂J=δi(L)ai(L−1)
对向量/矩阵运算:
δ
(
L
)
=
−
(
y
(
L
)
−
a
(
L
)
)
⊙
f
′
(
z
(
L
)
)
delta^{(L)} = -(y^{(L)}-a^{(L)})odot f'(z^{(L)})
δ(L)=−(y(L)−a(L))⊙f′(z(L))
▽
W
(
L
)
J
=
δ
(
L
)
(
a
(
L
−
1
)
)
T
bigtriangledown_{W^{(L)}}J = delta^{(L)}(a^{(L-1)})^T
▽W(L)J=δ(L)(a(L−1))T
再用这个式子进行权重的更新即可
隐藏层权重更新
隐藏层的权重更新也是使用链式法则求偏导数,只不过平时使用的都是向量而已:
对 w 11 ( 2 ) w^{(2)}_{11} w11(2)更新:
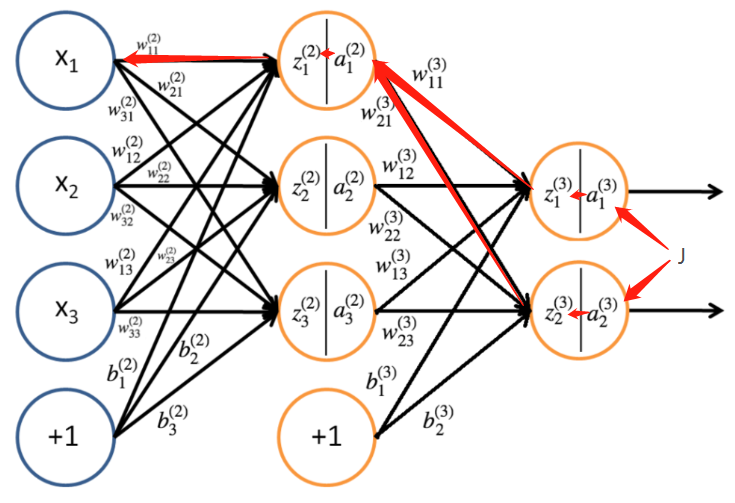
∂ J 3 ∂ w 11 ( 2 ) = ∂ J 3 ∂ a 1 ( 3 ) ∂ a 1 ( 3 ) ∂ z 1 ( 3 ) ∂ z 1 ( 3 ) ∂ a 1 ( 2 ) ∂ a 1 ( 2 ) ∂ z 1 ( 2 ) z 1 ( 2 ) w 11 ( 2 ) + ∂ J 3 ∂ a 2 ( 3 ) ∂ a 2 ( 3 ) ∂ z 2 ( 3 ) ∂ z 2 ( 3 ) ∂ a 1 ( 2 ) ∂ a 1 ( 2 ) ∂ z 1 ( 2 ) z 1 ( 2 ) w 11 ( 2 ) frac{partial J_3}{partial w^{(2)}_{11}}=frac{partial J_{3}}{partial a^{(3)}_1}frac{partial a^{(3)}_1}{partial z^{(3)}_1}frac{partial z^{(3)}_1}{partial a^{(2)}_{1}}frac{partial a^{(2)}_{1}}{partial z^{(2)}_1}frac{z^{(2)}_1}{w^{(2)}_{11}}+frac{partial J_{3}}{partial a^{(3)}_2}frac{partial a^{(3)}_2}{partial z^{(3)}_2}frac{partial z^{(3)}_2}{partial a^{(2)}_{1}}frac{partial a^{(2)}_{1}}{partial z^{(2)}_1}frac{z^{(2)}_1}{w^{(2)}_{11}} ∂w11(2)∂J3=∂a1(3)∂J3∂z1(3)∂a1(3)∂a1(2)∂z1(3)∂z1(2)∂a1(2)w11(2)z1(2)+∂a2(3)∂J3∂z2(3)∂a2(3)∂a1(2)∂z2(3)∂z1(2)∂a1(2)w11(2)z1(2)
再结合
其他隐藏层权重更新同理,在这里不再过多赘述
接着使用刚刚我们定义的 δ i ( l ) delta^{(l)}_i δi(l)推导公式
∂ J ∂ w i j ( l ) = ∂ J ∂ z i ( l ) = δ i ( l ) ∂ z i ( l ) w i j ( l ) = δ i ( l ) a j ( l − 1 ) frac{partial J}{partial w^{(l)}_{ij}}=frac{partial J}{partial z^{(l)}_i}=delta^{(l)}_ifrac{partial z^{(l)}_i}{w^{(l)}_{ij}}=delta^{(l)}_ia^{(l-1)}_j ∂wij(l)∂J=∂zi(l)∂J=δi(l)wij(l)∂zi(l)=δi(l)aj(l−1)
当在隐藏层时,又链式法则和函数和求导公式就有:
∂ J ∂ z i ( l ) = ∂ J ∂ z 1 ( l − 1 ) ∂ z 1 ( l − 1 ) ∂ z ( i ) + ∂ J ∂ z 2 ( l − 1 ) ∂ z 2 ( l − 1 ) ∂ z ( i ) + ⋅ ⋅ ⋅ + ∂ J ∂ z n l + 1 ( l − 1 ) ∂ z n l + 1 ( l − 1 ) ∂ z ( i ) = ∑ j = 1 n l + 1 ∂ J ∂ z j ( l + 1 ) ∂ z j l + 1 ∂ z i l frac{partial J}{partial z^{(l)}_i} = frac{partial J}{partial z^{(l-1)}_1}frac{partial z^{(l-1)}_1}{partial z^{(i)}}+frac{partial J}{partial z^{(l-1)}_2}frac{partial z^{(l-1)}_2}{partial z^{(i)}}+···+frac{partial J}{partial z^{(l-1)}_{n_l+1}}frac{partial z^{(l-1)}_{n_l+1}}{partial z^{(i)}}=sum^{n_l+1}_{j=1}frac{partial J}{partial z^{(l+1)}_j}frac{partial z^{l+1}_j}{partial z^{l}_i} ∂zi(l)∂J=∂z1(l−1)∂J∂z(i)∂z1(l−1)+∂z2(l−1)∂J∂z(i)∂z2(l−1)+⋅⋅⋅+∂znl+1(l−1)∂J∂z(i)∂znl+1(l−1)=j=1∑nl+1∂zj(l+1)∂J∂zil∂zjl+1
所以
$$ delta^{(l)}_i = frac{partial J}{partial z^{(l)}_i}=sum^{n_l+1}_{j=1}frac{partial J}{partial z^{(l+1)}_j}frac{partial z^{l+1}_j}{partial z^{l}_i}=sum^{n_l+1}_{j=1}delta^{(l+1)}_jfrac{partial z^{l+1}_j}{partial z^{l}_i} $$又因为
z j ( l + 1 ) = ∑ i = 1 n l w j i ( l + 1 ) a i ( l ) + b j ( l + 1 ) = ∑ i = 1 n l w j i ( l + 1 ) f ( z i ( l ) ) + b j ( l + 1 ) z^{(l+1)}_j=sum^{n_l}_{i=1}w^{(l+1)}_{ji}a^{(l)}_i+b^{(l+1)}_j = sum^{n_l}_{i=1}w^{(l+1)}_{ji}f(z^{(l)}_i)+b^{(l+1)}_j zj(l+1)=i=1∑nlwji(l+1)ai(l)+bj(l+1)=i=1∑nlwji(l+1)f(zi(l))+bj(l+1)
所以有:
∂ z j ( l + 1 ) ∂ z i ( l ) = ∂ z j ( l + 1 ) ∂ a i ( l ) ∂ a i ( l ) ∂ z j ( l ) = w j i ( l + 1 ) f z i ( l ) frac{partial z^{(l+1)}_j}{partial z^{(l)}_i}= frac{partial z^{(l+1)}_j}{partial a^{(l)}_i}frac{partial a^{(l)}_i}{partial z^{(l)}_j}=w^{(l+1)}_{ji}f{z^{(l)}_i} ∂zi(l)∂zj(l+1)=∂ai(l)∂zj(l+1)∂zj(l)∂ai(l)=wji(l+1)fzi(l)
再带入前面的 δ i ( l ) delta^{(l)}_i δi(l):
$$ delta^{(l)}_i = f'(z^{(l)}_i)sum^{n_l+1}_{j=1}delta^{(l+1)}_{j}w^{(l+1)}_{ji} $$ 对向量/矩阵运算: $$ delta^{(l)}_i = f'(z^{(l)}_i)odot (W^{(l+1)})^Tdelta^{(l+1)} $$输出层偏置更新
偏置的更新其实和权重更新是一样的
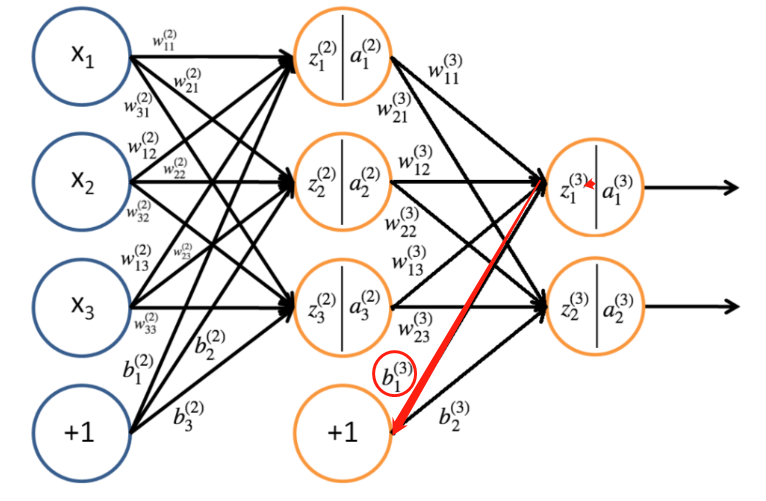
输出层的偏置比较好算
∂
J
∂
b
1
(
3
)
=
∂
J
∂
a
1
(
3
)
∂
a
1
(
3
)
∂
z
1
(
3
)
z
1
(
3
)
b
1
(
3
)
frac{partial J}{partial b^{(3)}_1} = frac{partial J}{partial a^{(3)}_1}frac{partial a^{(3)}_1}{partial z^{(3)}_1}frac{z^{(3)}_1}{b^{(3)}_1}
∂b1(3)∂J=∂a1(3)∂J∂z1(3)∂a1(3)b1(3)z1(3)
∂
J
∂
b
2
(
3
)
=
∂
J
∂
a
2
(
3
)
∂
a
2
(
3
)
∂
z
2
(
3
)
z
2
(
3
)
b
2
(
3
)
frac{partial J}{partial b^{(3)}_2} = frac{partial J}{partial a^{(3)}_2}frac{partial a^{(3)}_2}{partial z^{(3)}_2}frac{z^{(3)}_2}{b^{(3)}_2}
∂b2(3)∂J=∂a2(3)∂J∂z2(3)∂a2(3)b2(3)z2(3)
再结合
隐藏层偏执更新
隐藏层偏置更新和权重更新也是一个道理
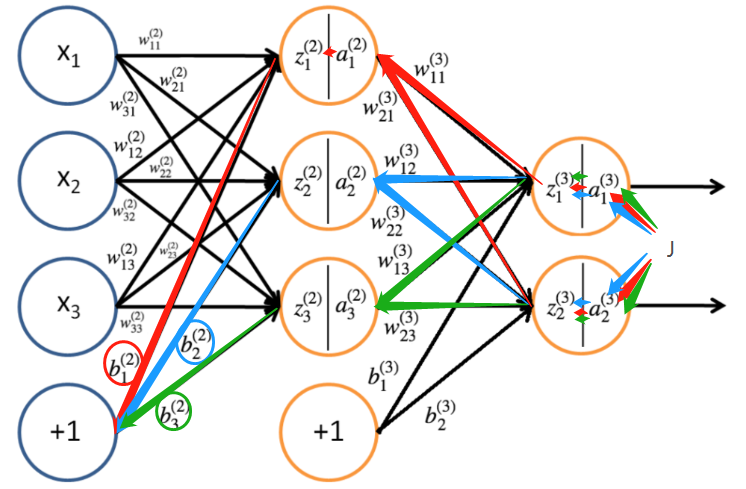
∂
J
∂
b
1
(
2
)
=
∂
J
∂
a
1
(
3
)
∂
a
1
(
3
)
∂
z
1
(
3
)
z
1
(
3
)
a
1
(
2
)
a
1
(
2
)
z
1
(
2
)
z
1
(
2
)
b
1
(
2
)
+
∂
J
∂
a
2
(
3
)
∂
a
2
(
3
)
∂
z
2
(
3
)
z
2
(
3
)
a
1
(
2
)
a
1
(
2
)
z
1
(
2
)
z
1
(
2
)
b
1
(
2
)
frac{partial J}{partial b^{(2)}_1} = frac{partial J}{partial a^{(3)}_1}frac{partial a^{(3)}_1}{partial z^{(3)}_1}frac{z^{(3)}_1}{a^{(2)}_1}frac{a^{(2)}_1}{z^{(2)}_1}frac{z^{(2)}_1}{b^{(2)}_1}+frac{partial J}{partial a^{(3)}_2}frac{partial a^{(3)}_2}{partial z^{(3)}_2}frac{z^{(3)}_2}{a^{(2)}_1}frac{a^{(2)}_1}{z^{(2)}_1}frac{z^{(2)}_1}{b^{(2)}_1}
∂b1(2)∂J=∂a1(3)∂J∂z1(3)∂a1(3)a1(2)z1(3)z1(2)a1(2)b1(2)z1(2)+∂a2(3)∂J∂z2(3)∂a2(3)a1(2)z2(3)z1(2)a1(2)b1(2)z1(2)
∂
J
∂
b
2
(
2
)
=
∂
J
∂
a
1
(
3
)
∂
a
1
(
3
)
∂
z
1
(
3
)
z
1
(
3
)
a
2
(
2
)
a
2
(
2
)
z
2
(
2
)
z
2
(
2
)
b
2
(
2
)
+
∂
J
∂
a
2
(
3
)
∂
a
2
(
3
)
∂
z
2
(
3
)
z
2
(
3
)
a
2
(
2
)
a
2
(
2
)
z
2
(
2
)
z
2
(
2
)
b
2
(
2
)
frac{partial J}{partial b^{(2)}_2} = frac{partial J}{partial a^{(3)}_1}frac{partial a^{(3)}_1}{partial z^{(3)}_1}frac{z^{(3)}_1}{a^{(2)}_2}frac{a^{(2)}_2}{z^{(2)}_2}frac{z^{(2)}_2}{b^{(2)}_2}+frac{partial J}{partial a^{(3)}_2}frac{partial a^{(3)}_2}{partial z^{(3)}_2}frac{z^{(3)}_2}{a^{(2)}_2}frac{a^{(2)}_2}{z^{(2)}_2}frac{z^{(2)}_2}{b^{(2)}_2}
∂b2(2)∂J=∂a1(3)∂J∂z1(3)∂a1(3)a2(2)z1(3)z2(2)a2(2)b2(2)z2(2)+∂a2(3)∂J∂z2(3)∂a2(3)a2(2)z2(3)z2(2)a2(2)b2(2)z2(2)
∂
J
∂
b
3
(
2
)
=
∂
J
∂
a
1
(
3
)
∂
a
1
(
3
)
∂
z
1
(
3
)
z
1
(
3
)
a
3
(
2
)
a
3
(
2
)
z
3
(
2
)
z
3
(
2
)
b
3
(
2
)
+
∂
J
∂
a
2
(
3
)
∂
a
2
(
3
)
∂
z
2
(
3
)
z
2
(
3
)
a
3
(
2
)
a
3
(
2
)
z
3
(
2
)
z
3
(
2
)
b
3
(
2
)
frac{partial J}{partial b^{(2)}_3} = frac{partial J}{partial a^{(3)}_1}frac{partial a^{(3)}_1}{partial z^{(3)}_1}frac{z^{(3)}_1}{a^{(2)}_3}frac{a^{(2)}_3}{z^{(2)}_3}frac{z^{(2)}_3}{b^{(2)}_3}+frac{partial J}{partial a^{(3)}_2}frac{partial a^{(3)}_2}{partial z^{(3)}_2}frac{z^{(3)}_2}{a^{(2)}_3}frac{a^{(2)}_3}{z^{(2)}_3}frac{z^{(2)}_3}{b^{(2)}_3}
∂b3(2)∂J=∂a1(3)∂J∂z1(3)∂a1(3)a3(2)z1(3)z3(2)a3(2)b3(2)z3(2)+∂a2(3)∂J∂z2(3)∂a2(3)a3(2)z2(3)z3(2)a3(2)b3(2)z3(2)
再根据对权重的推论,同理可得:
$$ delta^{(l)}_i = frac{partial J}{partial b^{(l)}_i}=frac{partial J}{partial z^{(l)}_i}frac{partial z^{(l)}_i}{b^{(l)}_i} $$ 对向量/矩阵运算: $$ delta^{l}=bigtriangledown_b^{(l)}J $$再结合:
最后
以上就是虚拟海燕最近收集整理的关于【学习笔记】BP神经网络学习简介信息前向传播误差反向传播的全部内容,更多相关【学习笔记】BP神经网络学习简介信息前向传播误差反向传播内容请搜索靠谱客的其他文章。








发表评论 取消回复