【人工神经网络学习笔记】理解BP算法——简单实例【人工神经网络】学习笔记BP算法讲解：前向映射+误差反向传播

68 阅读 0 评论 45 点赞

我是靠谱客的博主威武音响，最近开发中收集的这篇文章主要介绍【人工神经网络学习笔记】理解BP算法——简单实例【人工神经网络】学习笔记BP算法讲解：前向映射+误差反向传播，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

【人工神经网络】学习笔记

BP算法讲解：前向映射+误差反向传播

关键点：链式求导法则反复用

本文以一个实例理解误差反向传播过程。

转自https://blog.csdn.net/zhaomengszu/article/details/77834845感谢作者

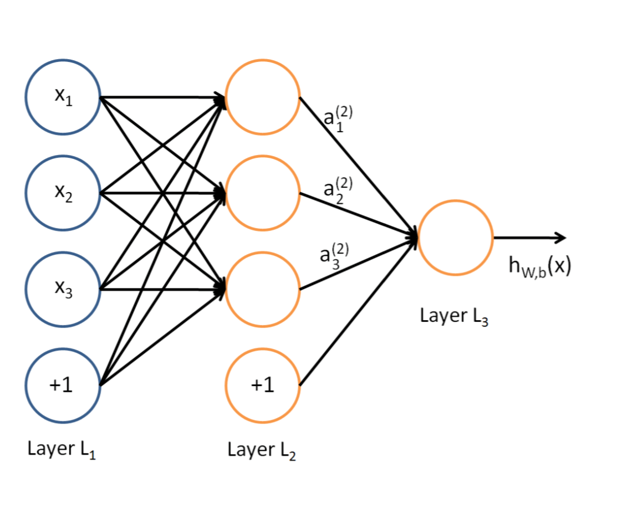
这是典型的三层神经网络的基本构成，Layer L1是输入层，Layer L2是隐含层，Layer L3是隐含层，我们现在手里有一堆数据{x1,x2,x3,…,xn},输出也是一堆数据{y1,y2,y3,…,yn},现在要他们在隐含层做某种变换，让你把数据灌进去后得到你期望的输出。如果你希望你的输出和原始输入一样，那么就是最常见的自编码模型（Auto-Encoder）。可能有人会问，为什么要输入输出都一样呢？有什么用啊？其实应用挺广的，在图像识别，文本分类等等都会用到，我会专门再写一篇Auto-Encoder的文章来说明，包括一些变种之类的。如果你的输出和原始输入不一样，那么就是很常见的人工神经网络了，相当于让原始数据通过一个映射来得到我们想要的输出数据，也就是我们今天要讲的话题。

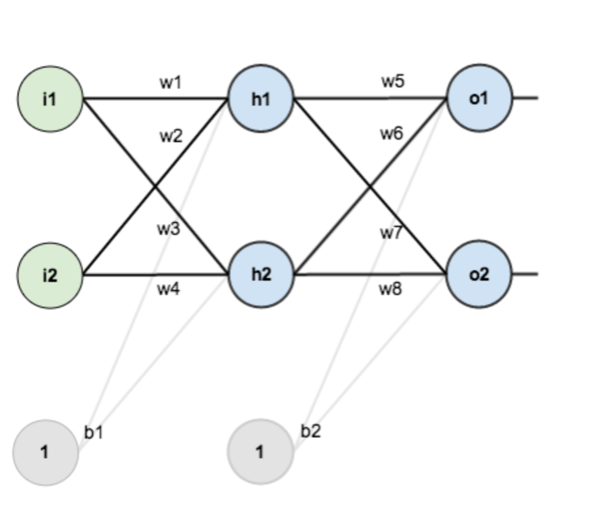
第一层是输入层，包含两个神经元i1，i2，和截距项b1；第二层是隐含层，包含两个神经元h1,h2和截距项b2，第三层是输出o1,o2，每条线上标的wi是层与层之间连接的权重，激活函数我们默认为sigmoid函数。

现在对他们赋上初值，如下图：

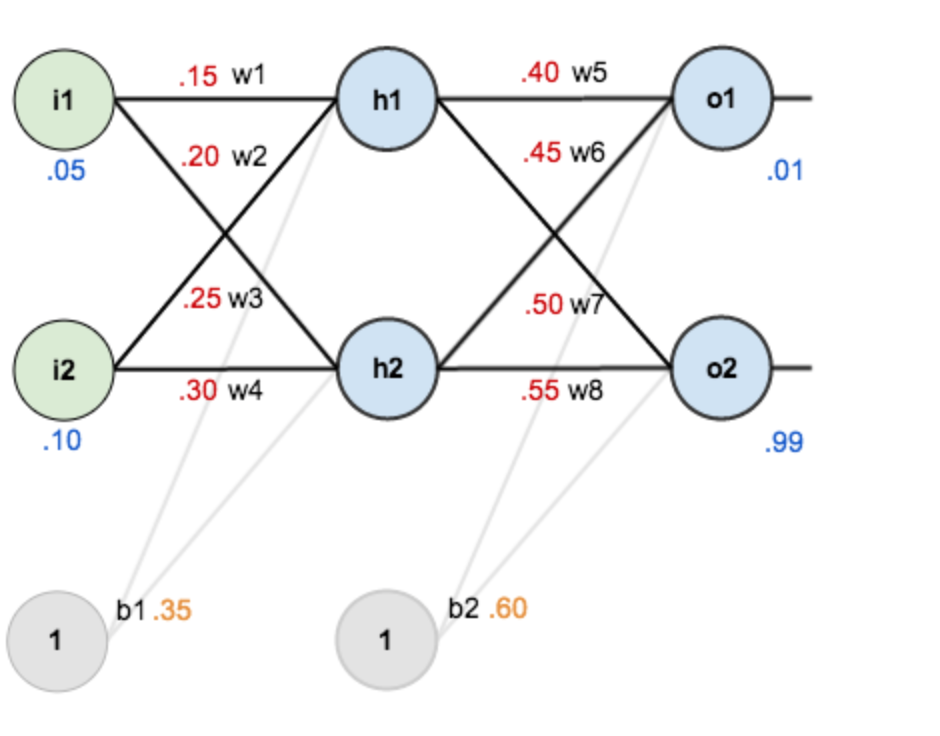
其中，输入数据 i1=0.05，i2=0.10;

输出数据 o1=0.01,o2=0.99;

初始权重 w1=0.15,w2=0.20,w3=0.25,w4=0.30;

w5=0.40,w6=0.45,w7=0.50,w8=0.55

　　目标：给出输入数据i1,i2(0.05和0.10)，使输出尽可能与原始输出o1,o2(0.01和0.99)接近。

Step 1 前向传播

　　1.输入层—->隐含层：

　　计算神经元h1的输入加权和：

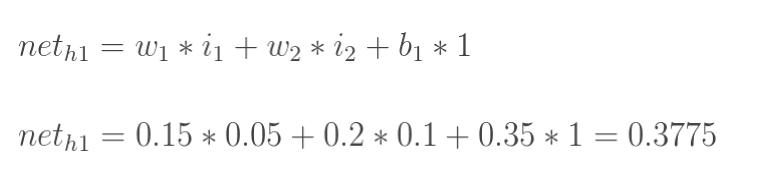
神经元h1的输出o1:(此处用到激活函数为sigmoid函数)：

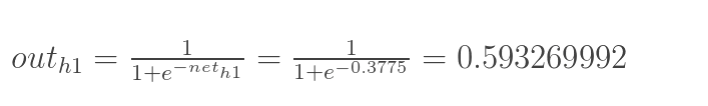
　　同理，可计算出神经元h2的输出o2：

　　2.隐含层—->输出层：

　　计算输出层神经元o1和o2的值：

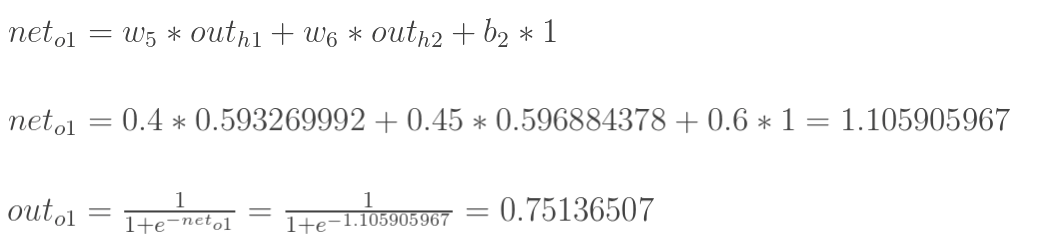
这样前向传播的过程就结束了，我们得到输出值为[0.75136079 , 0.772928465]，与实际值[0.01 , 0.99]相差还很远，现在我们对误差进行反向传播，更新权值，重新计算输出。

Step 2 反向传播

1.计算总误差

总误差：(square error)

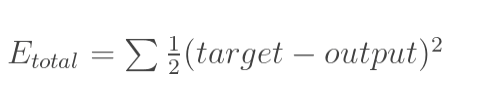
但是有两个输出，所以分别计算o1和o2的误差，总误差为两者之和：

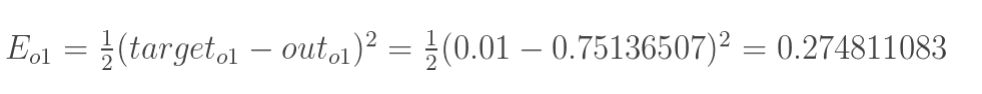
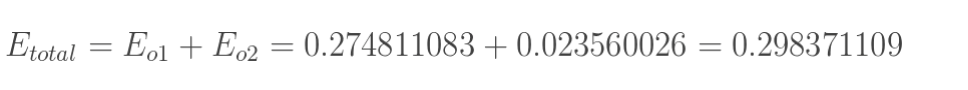
2.隐含层—->输出层的权值更新：

以权重参数w5为例，如果我们想知道w5对整体误差产生了多少影响，可以用整体误差对w5求偏导求出：（链式法则）

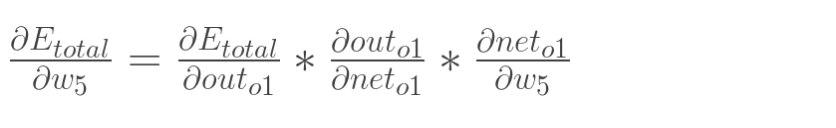
下面的图可以更直观的看清楚误差是怎样反向传播的：

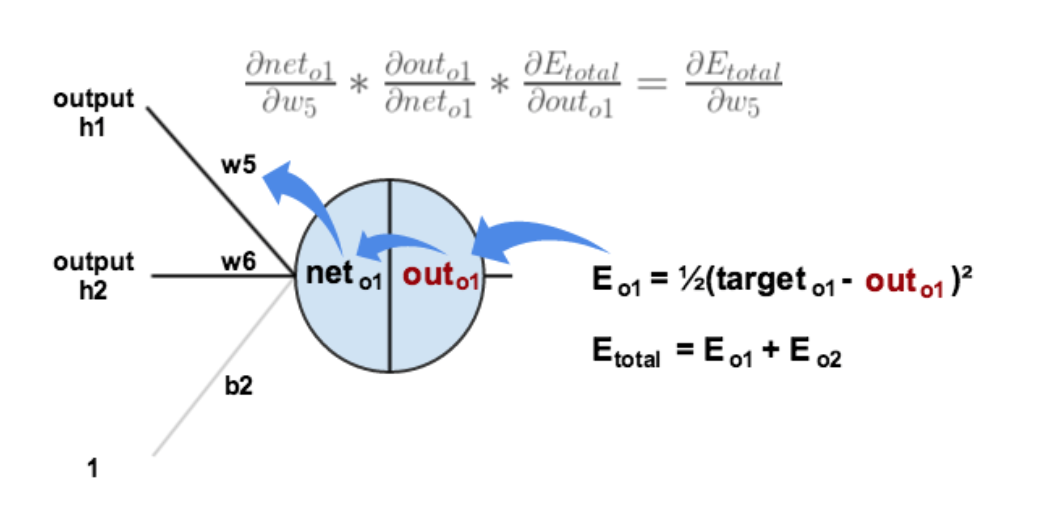
现在我们来分别计算每个式子的值：

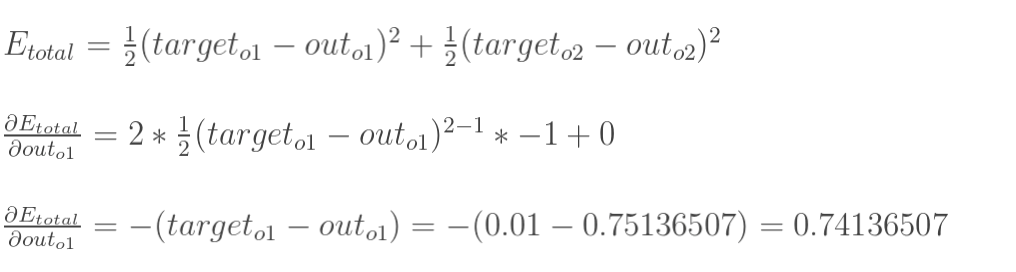
计算：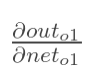

采用S型函数的好处：其导数是其本身的函数，避免计算机求导计算。

（这一步实际上就是对sigmoid函数求导，比较简单，可以自己推导一下）

计算：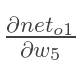

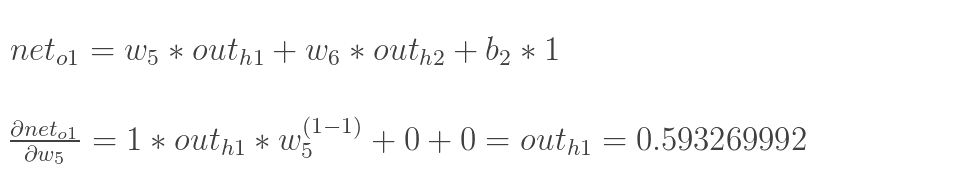
最后三者相乘：

这样我们就计算出整体误差E(total)对w5的偏导值。

回过头来再看看上面的公式，我们发现：

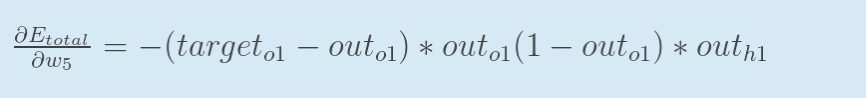
为了表达方便，用来表示输出层的误差：

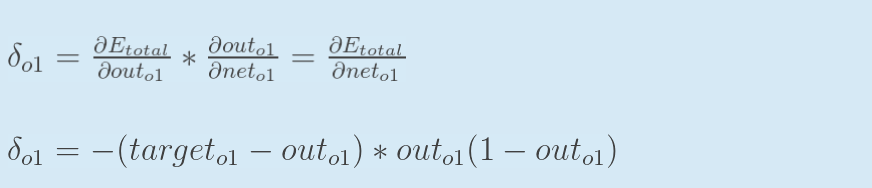
因此，整体误差E(total)对w5的偏导公式可以写成：

如果输出层误差计为负的话，也可以写成：

最后我们来更新w5的值：

（其中，是学习速率，这里我们取0.5）

同理，可更新w6,w7,w8:

3.隐含层—->隐含层的权值更新：

　方法其实与上面说的差不多，但是有个地方需要变一下，在上文计算总误差对w5的偏导时，是从out(o1)—->net(o1)—->w5,但是在隐含层之间的权值更新时，是out(h1)—->net(h1)—->w1,而out(h1)会接受E(o1)和E(o2)两个地方传来的误差，所以这个地方两个都要计算。

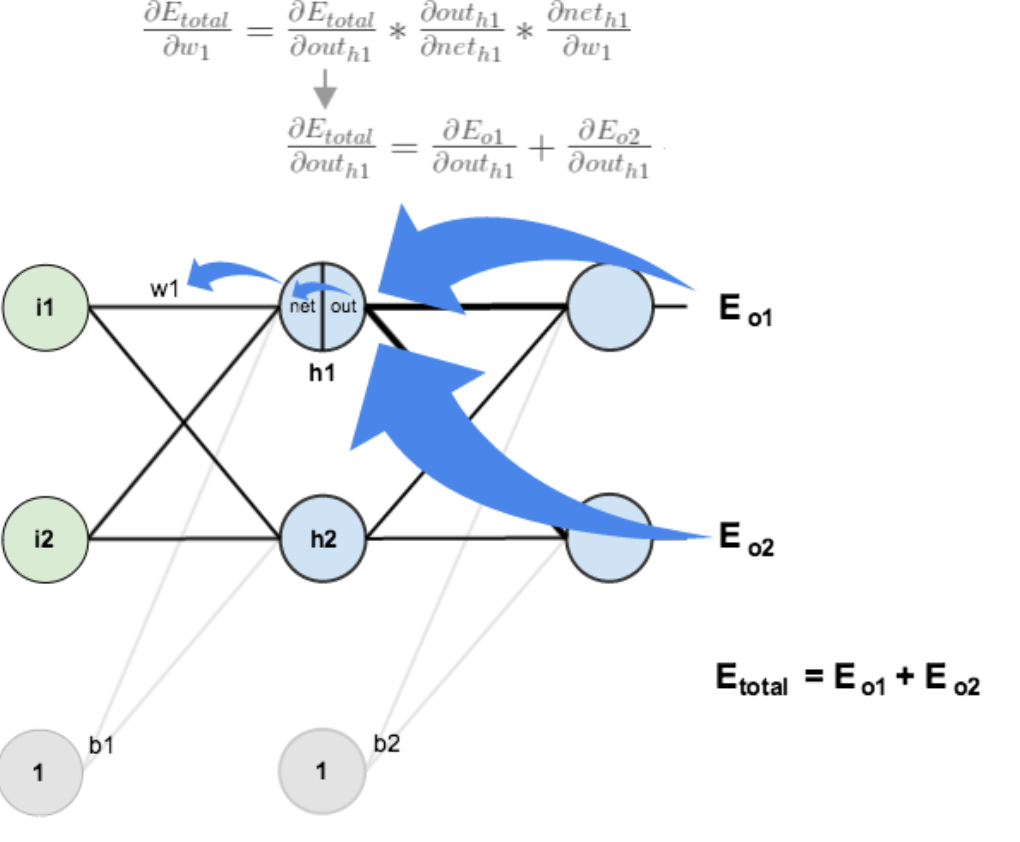
计算：

先计算：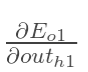

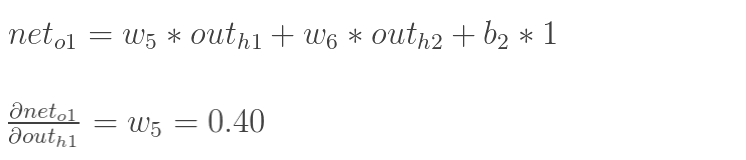
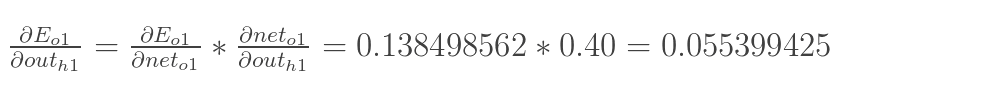
同理，计算出：

两者相加得到总值：

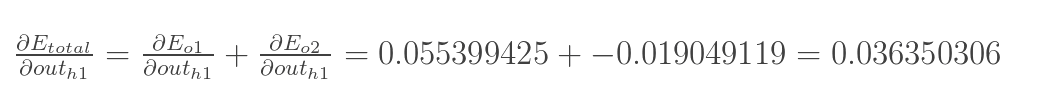
再计算：

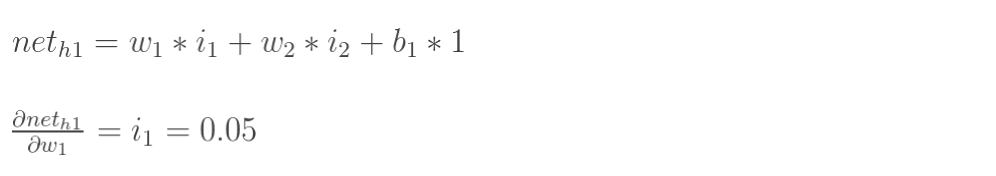
最后，三者相乘：

为了简化公式，用sigma(h1)表示隐含层单元h1的误差：

最后，更新w1的权值：

同理，额可更新w2,w3,w4的权值：

　　这样误差反向传播法就完成了，最后我们再把更新的权值重新计算，不停地迭代，在这个例子中第一次迭代之后，总误差E(total)由0.298371109下降至0.291027924。迭代10000次后，总误差为0.000035085，输出为[0.015912196,0.984065734](原输入为[0.01,0.99]),证明效果还是不错的。

补充：

权值更新的过程中更新规则是：

1.当误差对权值的偏导数大于0时，权值调整量为负，实际输出大于期望输出，权值向减少的方向调整，使得实际输出与期望输出的差减小。

2.当误差对权值的偏导数小于0时，权值调整量为正，实际输出小于期望输出，权值向增大的方向调整，使得实际输出与期望输出的差减小。

总结：

BP神经网络实现了输入到输出的非线性映射，给了新的非样本数据依然可以做出正确的映射，具有一定的泛化能力和容错能力。
有监督的学习算法，学习算法采用的梯度下降算法，权值越多，局部极小点越多。
全局逼近
权值调整的快慢与梯度搜索算法的步长有关，收敛速度与权值的初始值有关。
网络的结构设计（隐层的层数、隐层节点的个数等）无理论指导。
激活函数采用S型函数时，存在平坦区域即误差下降缓慢的区域，影响收敛速度。因此有大范围样本的时候，常常对输入样本进行归一化，使得数据分布在梯度下降较大的区域，加快其收敛速度。最终的输出也做相应处理。

目前改进的BP网络的学习算法有：消除样本输入顺序影响的改进算法、附加动量的改进算法、采用自适应调整参数的改进算法、使用弹性方法的改进算法等。