麦克纳姆轮

图1

图2

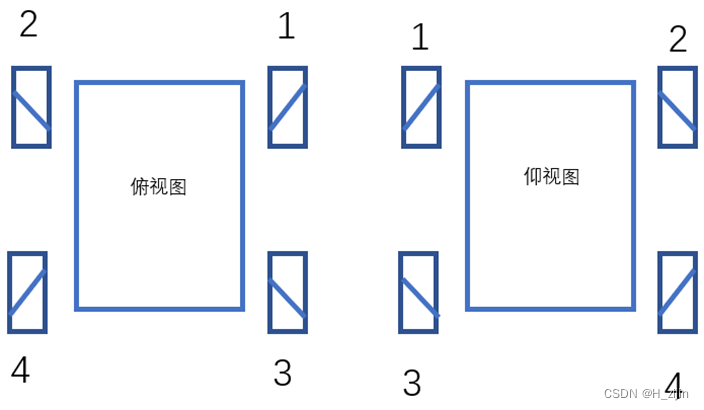
图3

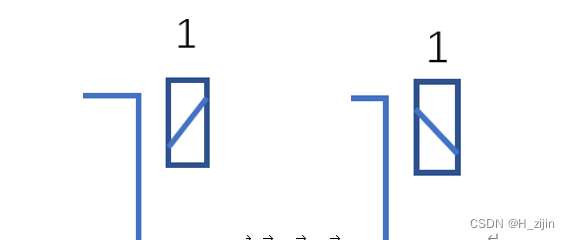
                                                       图4                                 图5

        麦克纳姆轮的安装如图1所示。暂定以图1中向上为小车的正方向（即前方），右上角为1号车轮、左上角为2号车轮、右下角为3号车轮、左下角为4号车轮。每号车轮上的小滚轮称对应车轮的小轮。图2是对图1绕小车正方向的轴旋转180°的结果。

简化后如图3所示（注意看每号车轮上小轮的方向）。对麦克纳姆轮的观察我们可以知道，1号轮子的俯视图如图4所示。但是1号轮的小轮与地面的接触那一侧的方向与我们俯视小车看到的不同。在俯视图上标记1号轮子的小轮接触地面这一平面的方向，如图5所示。我们在小车俯视图中的每号车轮上标记出与地面接触这一平面的小轮方向如图6所示。

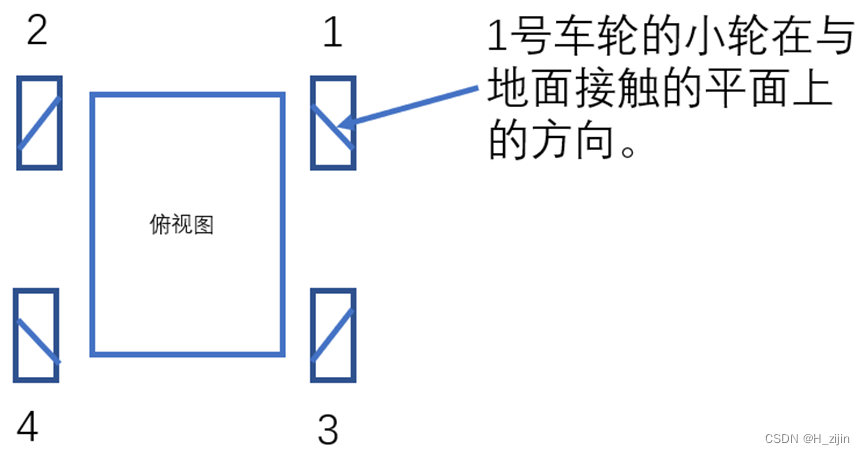
图6

运动分析及反求轮速

在分析过程中提出几点假设：

1. 车轮与地面不存在打滑。
2. 小轮倾斜的角度为45°。

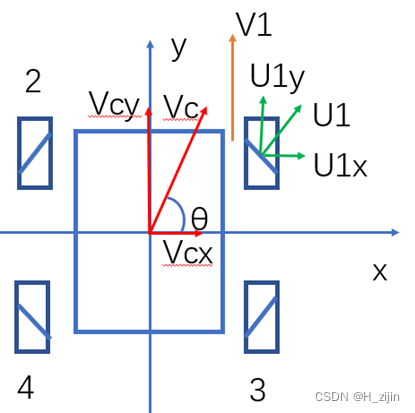
图7

如图7所示。小车的速度为Vc(读作V车)，的方向是θ。在x轴的分量为Vcx，在y轴的分量为Vcy。

设小车1号轮子的转速为V1，1号车轮上的小轮的转速为u1（它是朝向右前方45°的）同样u1也有x和y轴的分量u1x和u1y。

由于整个小车的速度是由V1和u1合成。

且V1没有x轴分量。

所以有小车x轴方向速度分量等于小轮的x轴方向速度分量。

Vcx=u1x=u1cos45                                                              (1)

小车y轴方向速度分量等于小轮的y轴方向速度分量与1号车轮的速度叠加。

Vcy=V1+u1y=V1+u1sin45                                                       (2)

由（1）（2）式化简消去u1

V1=Vcy-Vcx                                                                    (3)

显然有

                                                             Vcx=Vccosθ 

                                                             Vcy=Vcsinθ 

所以

                                                      V1=（sinθ-cosθ）Vc

同理可得2号车轮得速度为

                                                      V2=（cosθ+sinθ）Vc 

当保持小车车头方向不变，向任意θ角度方向移动是，1号车轮和4号车轮的运动情况一致，2号车轮和3号车轮的运动情况一致。他们的速度与θ的关系如图8所示

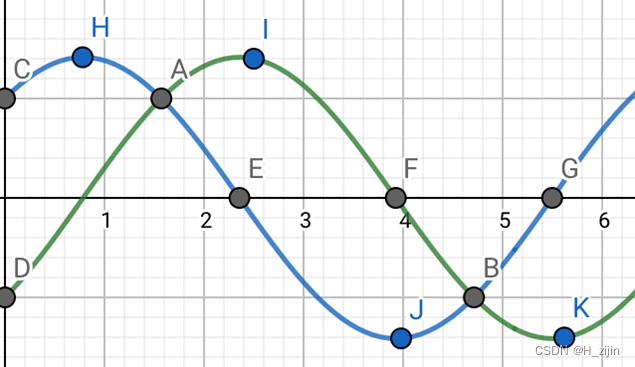
图8横坐标为Vc与x轴的夹角θ，纵轴为（1号和2号）车轮的速度

到此，理论上可以实现小车保持车头方向不变的情况下做360度平动。

然而事实上，我们还需要加上PID控制来保证车轮达到我们预期的速度。同时为了确保小车的朝向不发生改变，还要利用传感器（如mpu）对小车朝向进行调整。

最后

以上就是虚拟海燕最近收集整理的关于麦克纳姆轮小车360°平动的全部内容，更多相关麦克纳姆轮小车360°平动内容请搜索靠谱客的其他文章。