摘自：

https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/classes/cs294_f99/notes/lec7/lec7.htm

Gibbs Distribution

            

 

Proving Gibbs Distribution Implies Markov Random Field

 

1. 

 

Trivial because of exponential

 

1. 

 

 

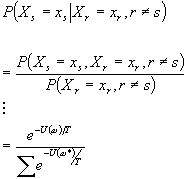
            Look at the handout given in class for a detailed proof.

            In summary, at the end of the day, sites without s cancel.

 

 

Back to the Image Segmentation Problem

                                                      

Our image model

 

	true image f

 

 

 

 

 

            line process l not observed

 

Goal

 

• Given observed image g, find a probability distribution of true image f, and the line process l.

 

            The line process estimate solves the image segmentation problem.

            The true image estimate solves the image restoration problem.

            Both problems are simultaneously solved!

 

• Note: only works for piecewise smoothe images Þ no textures

 

 

Our model assumes:

 

            

 

Our solution:

 

 

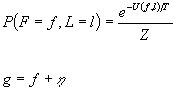
prior distribution

            

 

 

 

 

 

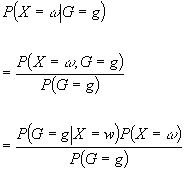
Interesting term:

 

 

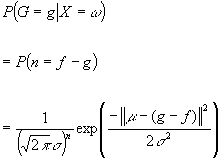
            Where we assume every pixel has independent noise h ~ N ( m , s )

            e.g. Poisson process noise in CCDs

 

Result:

            

 

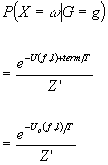
            is the posterior probability of a particular f, l given g. Note this is also a Gibbs distribution!

 

MAP (maximum a posteriori) Estimate

 

            If you insist on a single answer then return f*,  l* that maximizes

                        

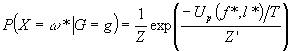
            or equivalently, minimizes the energy function

           

                        

 

            Problem:           f , l space is very large!!

Solution:           Construct samples of f , l in this space with high probablity

Technique:        Markov Chain Monte Carlo (MCMC) lets you sample the posterior distribution

 

 

Sampling a Distribution

 

            Q:        How do we represent a probability distribution with sampling?

            A:         Create many samples drawn from that distribution and count!

 

            Example:

 

            Q:        P(X > 17) = ?

            A:         Create samples Xi drawn from the distribution of X.

                        

            Count the number of samples greater than 17 and divide by total number of samples.

 

Generating the Samples

 

            Primitive random number generator X ~ U(0,1).

            To create Y ~ U(a,b) use

           

            Y = a + ( b – a ) X

 

            In general we can use the cumulative distribution function

 

            

 

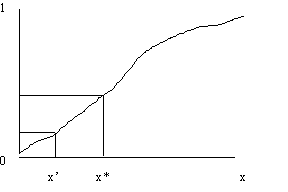
            1987 – Stochastic Simulation (Ripley) for generating samples for “standard stuff” in textbooks

 

Markov Chain Monte Carlo (MCMC) Technique

 

• Define a suitable Markov Chain whose equilibrium distribution is the desired posterior distribution
• Generate samples from the Markov Chain

 

Markov Chain Basics

 

            

 

            Example:

            

 

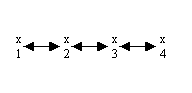
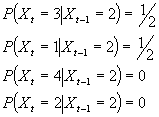
This transition probabilities can be written as a matrix

 

 

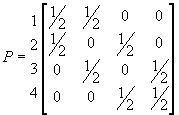
            If we write the probability distribution at time t as p(t) then

 

            p(t+1) = p(t)P

           

            For example if the drunk’s walk starts at position 2 we denote

            p( t = 0 ) = [0 1 0 0]

 

            p(t) is an evolving probability distribution which is a row vector that sums to one

 

            The equilibrium distribution p(infinity) = p satisfies

                        pP = p

            and is a left eigenvector of P with eigenvalue one.

           

Finding the Markov Chain Corresponding to the Posterior Distribution

                                                       

            Metropolis Sampler – Rosenberg, Teller, Teller

            Heat Bath ( Gibbs Sampler ) – “rapidly mixing” determines convergence rate

 

Metropolis Sampler

 

            We are given that the posterior distribution is of the form f(x)/Z

 

1.      We have a proposal kernal satisfying K(x,y) = K(y,x)

2.      Calculate f(y)

3.      Accept transition with probability = min {1, f(y)/f(x) }

4.      This eventually converges to the “right thing”

最后

以上就是粗犷小甜瓜为你收集整理的Gibbs Distribution, MRF, MCMCGibbs Distribution            Proving Gibbs Distribution Implies Markov Random Field的全部内容，希望文章能够帮你解决Gibbs Distribution, MRF, MCMCGibbs Distribution            Proving Gibbs Distribution Implies Markov Random Field所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。