MCMC与GIBBS算法学习记录

首先网上有很多资料，看了好久才看懂，现在把当时的不解强调一下，并大概把算法思路描述如下：

MCMC算法

第一个MC: Monte Carlo(蒙特卡洛)。第二个MC：Markov Chain(马尔科夫链)。

算法的目的是：在知道某一随机分布的概率密度函数和有一些它的采样情况下用计算机来生成这个随机分布的样本。比如用python的函数可以生成均匀分布、高斯分布的数据，现在我给你一个其它分布的概率密度函数，你用计算机给我写一个函数，这个函数可以生成随机数，随机数是目标分布。

基本原理与思路：

主要统计性质不随时间而变的马尔科夫链就可以认为是平稳的。数学上有马氏链收敛定理，当步长n足够大时，一个非周期且任意状态联通的马氏链可以收敛到一个平稳分布π(x)。这个定理就是所有的MCMC方法的理论基础。

定义：Markov链有转移概率矩阵P，如果有一个概率分布{πi}满足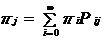,则称为这个Markov链的平稳分布。这个定义用矩阵形式写出来就是π*P=π.

具体操作方法：

假如目标分布是T（x），那么你要写一个生成这个分布的代码。首先要有概率密度，有了概率密度肯定就有值域.然后网上的方法是，从值域取出一个数据，由于我有概率密度，我自然知道这个数据的概率密度。然后用正太分布以这个数据为期望，方差为1，生成另外一个数，然后用构造出来的马尔科夫链转移矩阵来计算转移概率，再用均匀分布生成一个【0，1】随机数。若转移概率大于随机数则接受转移后的数，持续此过程5000次。基本上网上的代码就是这样编写的。

参考资料：http://blog.csdn.net/google19890102/article/details/51755242

Metropolis-Hastings是MCMC的改进，MCMC只能采样对称分布，而改进后无此要求，此算法只是对构造转移矩阵的函数进行了改进，其它不变。

以上是单维随机变量采样，可以推广到多维情况。说到推广则涉及到算法的本质。

算法的本质是，比如我想得到分布A的样本，并且我有一个A的样本，我认为A的变化有马尔科夫性，因此构造一个A的平稳马尔科夫链，然后不断的模拟它转移的过程，转移必然有一个转移后的值和转移概率。转移后的值如何选取来说其实网上的大多数中文文献都没有说明，只是有的代码里是用以待转移数据为期望、方差为1的高斯分布作为转移后的值的选取方式，当然你有转移后的值以后就有了转移概率，那么虽然我有概率，但是我仍旧决定不了我是否接受转移，这个阈值到底是多大也没有人说明，看代码是采用【0，1】均匀分布随机取值。然后就是接受转移或不接受。

因此多维情况下，同样是随机生成转移值，计算转移概率，生成转移阈值，接受或不接受。多维情况不同就是可以实施两种策略，一维一维的转移还是所有维度一起转移。基本思路还是算法的本质没变。

————————————————————————————————————————————————————

GIBBS算法

看了多篇文献后这个感觉最好：http://blog.sina.com.cn/s/blog_13dd6d82a0102vcio.html

通过改造转移矩阵，让每次的转移概率都是1，这样会使收敛速度变快。我的疑问是那为什么我不直接修改接受转移的概率？

最后

以上就是清脆胡萝卜为你收集整理的MCMC与GIBBS算法学习记录的全部内容，希望文章能够帮你解决MCMC与GIBBS算法学习记录所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。