模拟退火算法浅析

53 阅读 0 评论 35 点赞

我是靠谱客的博主苗条柚子，最近开发中收集的这篇文章主要介绍模拟退火算法浅析，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

模拟退火是一个比较好理解的算法。简单来讲就是模拟一个金属融化前温度很高，之后在空气中慢慢降温，同时内部的能量也越来越小，分子越来越趋于有序的这样一个模型。

初始温度为t0

结束温度tend

降温速率q（0<q<1）

初始温度为t0（这个参数是自己设立的，要尽量大一点，直接决定了训练次数，直观上讲训练次数越大得到的解应该越好），然后这个温度下对应有组参数（这个是系统自动生成的，随机生成的规则也能自己定），他们组成了矩阵x，首先判断当前温度是否小于等于结束温度tend,如果小于等于则结束程序，如果大于，则代入一个函数f(x0)后，算出函数值，就叫适应度函数吧，表达的意义和遗传算法类似。然后通过一个newanswer的函数去改变你输入的x矩阵，得到一个新的矩阵x1可以是打乱顺序啊，也可以是某一部分x上加上一个值，这个是根据具体问题来自己定的一个函数，这是最关键的函数，直接决定了这个模型的性能怎么样。然后算出来的新的f(x1)，判断适应度函数比之前大还是小，如果小就用保留x1，不再用x0,如果比之前大，则采用metropolis法则产生一个概率去决定是否保留。一个过程完成后，t0*q降温变成t1，变成了新的当前温度，,之后再重复上述过程，直到满足当前温度小于tend。

（手机版上的日志显示有格式bug...，好像会有文字错位和重叠的毛病。）

我们接下来解决一个很简单的问题，有十四个城市，x,y坐标固定，找到一个顺序旅行所有城市并最后回到自己的出发点，使得旅行的总距离最短。（当然这对聪明的小伙伴们来说是分分钟的事，但现在咱们让计算机自己算，看看会怎么样）

主程序代码（只是main.m，阐释主逻辑）：

%% I. 清空环境变量

clear all

clc

%% II. 导入城市位置数据

X = [16.4700 ...

96.1000

16.4700 94.4400

20.0900 92.5400

22.3900 93.3700

25.2300 97.2400

22.0000 96.0500

20.4700 97.0200

17.2000 96.2900

16.3000 97.3800

14.0500 98.1200

16.5300 97.3800

21.5200 95.5900

19.4100 97.1300

20.0900 92.5500];

%% III. 计算距离矩阵

D = Distance(X); %计算距离矩阵

N = size(D,1); %城市的个数

%% IV. 初始化参数

T0 = 1e10; % 初始温度

Tend = 1e-30; % 终止温度

L = 2; % 各温度下的迭代次数

q = 0.9; %降温速率

Time = ceil(double(solve([num2str(T0) '*(0.9)^x = ',num2str(Tend)]))); % 计算迭代的次数

% Time = 132;

count = 0; %迭代计数

Obj = zeros(Time,1); %目标值矩阵初始化

track = zeros(Time,N); %每代的最优路线矩阵初始化

%% V. 随机产生一个初始路线

S1 = randperm(N);

DrawPath(S1,X)

disp('初始种群中的一个随机值:')

OutputPath(S1);

Rlength = PathLength(D,S1);

disp(['总距离：',num2str(Rlength)]);

%% VI. 迭代优化

while T0 > Tend

count = count + 1; %更新迭代次数

temp = zeros(L,N+1);

% 1. 产生新解

S2 = NewAnswer(S1);

% 2. Metropolis法则判断是否接受新解

[S1,R] = Metropolis(S1,S2,D,T0); %Metropolis 抽样算法

% 3. 记录每次迭代过程的最优路线

if count == 1 || R < Obj(count-1)

Obj(count) = R; %如果当前温度下最优路程小于上一路程则记录当前路程

else

Obj(count) = Obj(count-1);%如果当前温度下最优路程大于上一路程则记录上一路程

end

track(count,:) = S1;

T0 = q * T0; %降温

end

%% VII. 优化过程迭代图

figure

plot(1:count,Obj)

xlabel('迭代次数')

ylabel('距离')

title('优化过程')

%% VIII. 绘制最优路径图

DrawPath(track(end,:),X)

%% IX. 输出最优解的路线和总距离

disp('最优解:')

S = track(end,:);

p = OutputPath(S);

disp(['总距离：',num2str(PathLength(D,S))]);

所有代码及其说明：

说明：%##到下一个%##，表示这一段在主文件里面本来没有，可能是在文档中新加的注释，也可能是另一个文件中的内容。PS:MATLAB里面要把函数单独放在一个函数文件中进行调用。

%% I. 清空环境变量

clear all

clc

%% II. 导入城市位置数据

X = [16.4700 96.1000

16.4700 94.4400

20.0900 92.5400

22.3900 93.3700

25.2300 97.2400

22.0000 96.0500

20.4700 97.0200

17.2000 96.2900

16.3000 97.3800

14.0500 98.1200

16.5300 97.3800

21.5200 95.5900

19.4100 97.1300

20.0900 92.5500];

%##

说明：这是城市的坐标数据，城市看成点，其实就是求14个点连起来的直线的最短长度。

%##

%% III. 计算距离矩阵

D = Distance(X); %计算距离矩阵

%##

说明：Distance函数单独列出一个函数文件来存放

%##

function D = Distance(citys)

%% 计算两两城市之间的距离，比如第一行第三列的数据表示的是第一个城市和第三个城市之间的距离。当然肯定有人会说第三行第一列不是一样的，确实是一样的，下面的循环有一个D(I,J)=D(J,I)的操作就是由此而来。

% 输入 citys 各城市的位置坐标

% 输出 D 两两城市之间的距离

n = size(citys,1);%citys指代的其实就是之前的x矩阵，把citys的行数返回给n,就是城市的个数。

D = zeros(n,n);%构造一个n*n的零阵。

for i = 1:n

for j = i+1:n

D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));%其实就是（x1-x2）^2+(y1-y2)^2之和开根号。

D(j,i) = D(i,j);%产生一个上三角对称矩阵，对角线上元素全为0。

end

N = size(D,1); %城市的个数

%% IV. 初始化参数

T0 = 1e10; % 初始温度

Tend = 1e-30; % 终止温度

L = 2; %各温度下的迭代次数(这个东西在程序里面没有用到，增加次数时可以用，程序里面其实L=1)

q = 0.9; %降温速率

Time = ceil(double(solve([num2str(T0) '*(0.9)^x = ',num2str(Tend)]))); % 计算迭代的次数

%##

这个solve函数是用来解方程的语法，非常重要。各个独立的字符串之间要有空格或者逗号。

%##

% Time = 132;

count = 0; %迭代计数

Obj = zeros(Time,1); %目标值矩阵初始化（就是用零阵创建一个矩阵，至于用1阵创建还是用0阵创建就随你了。）

track = zeros(Time,N); %每代的最优路线矩阵初始化（就是用零阵创建一个矩阵，至于用1阵创建还是用0阵创建就随你了。）

%% V. 随机产生一个初始路线

S1 = randperm(N);

DrawPath(S1,X)

%##

对DrawPath 函数文件做出说明：

function DrawPath(Route,citys)

%% 画路径函数

%输入

% Route 待画路径

% citys 各城市坐标位置

figure

plot([citys(Route,1);citys(Route(1),1)],... %‘...’是matlab里面的换行符号，相对于python来说就是

[citys(Route,2);citys(Route(1),2)],'o-');%在该行代码末尾加上续行符“”，即空格加上

grid on %grid on在图画上产生网格，’o-’是对图像特征的描述，后面

%会介绍。

for i = 1:size(citys,1) %for循环，i从1到citys的行数

text(citys(i,1),citys(i,2),[' ' num2str(i)]);%text函数，后面会介绍。

end

text(citys(Route(1),1),citys(Route(1),2),' 起点');

text(citys(Route(end),1),citys(Route(end),2),' 终点');

%x(end,1);x(end,2)分别表示x矩阵最后一行的第一列，和最后一行的第二列的元素

%##DrawPath函数文件结束

disp('初始种群中的一个随机值:')%在命令行窗口中打出这一行文字或者是字符。

OutputPath(S1);

%##说明该函数单独存在一个名为OutputPath.m的函数文件中

function p = OutputPath(R)

%% 输出路径函数

% 输入：R 路径

R = [R,R(1)];

N = length(R);

p = num2str(R(1));

for i = 2:N

p = [p,'—>',num2str(R(i))];%把p变为一个字符串，中括号里面用逗号隔开，这是一个非常

End %巧妙的算法，不断在一个区间后面加字符。

disp(p)

%##

Rlength = PathLength(D,S1);

%##

说明：该函数单独存在于一个PathLength.m的函数文件。

function Length = PathLength(D,Route)

%% 计算各个体的路径长度

% 输入：

% D 两两城市之间的距离

% Route 个体的轨迹

Length = 0;

n = size(Route,2);

for i = 1:(n - 1)

Length = Length + D(Route(i),Route(i + 1));

end

Length = Length + D(Route(n),Route(1));%最后一个是求最后一个到第一个的距离，违反了上面for循环

%## %的迭代规则，所以单独写出来。

disp(['总距离：',num2str(Rlength)]);

%% VI. 迭代优化

while T0 > Tend

count = count + 1; %更新迭代次数

temp = zeros(L,N+1); %

% 1. 产生新解

S2 = NewAnswer(S1);

%##

说明：该函数存在一个名为NewAnswer.m的函数文件中。

function S2 = NewAnswer(S1)

%% 输入

% S1:当前解

%% 输出

% S2：新解

N = length(S1);

S2 = S1;

a = round(rand(1,2)*(N-1)+1); %产生两个随机位置用来交换

W = S2(a(1));

S2(a(1)) = S2(a(2));

S2(a(2)) = W; %得到一个新路线

%##

% 2. Metropolis法则判断是否接受新解

%##

说明：

若在温度T，当前状态i → 新状态j

若Ej<Ei，则接受 j 为当前状态；

否则，若概率 p=exp[-(Ej-Ei)/KT] 大于[0,1)区间的随机数，则仍接受状态 j 为当前状态；若不成立，则保留状态 i 为当前状态。

%##

[S1,R] = Metropolis(S1,S2,D,T0); %Metropolis 抽样算法

%##

说明：以下存在于Metropolis.m函数文件中的函数Metropolis

function [S,R] = Metropolis(S1,S2,D,T)

%% 输入

% S1：当前解

% S2: 新解

% D: 距离矩阵（两两城市的之间的距离）

% T: 当前温度

%% 输出

% S：下一个当前解

% R：下一个当前解的路线距离

R1 = PathLength(D,S1); %计算前一条路线长度

N = length(S1); %得到城市的个数

R2 = PathLength(D,S2); %计算新的路线长度

dC = R2 - R1; %计算能力之差

if dC < 0 %如果能力降低接受新路线

S = S2;

R = R2;

elseif exp(-dC/T) >= rand %以exp(-dC/T)概率接受新路线

S = S2;

R = R2;

else %不接受新路线

S = S1;

R = R1;

end

%##

% 3. 记录每次迭代过程的最优路线

if count == 1 || R < Obj(count-1) %count==1是考虑到初始状态没有上一次路程。

Obj(count) = R; %如果当前温度下最优路程小于上一路程则记录当前路程

else

Obj(count) = Obj(count-1);%如果当前温度下最优路程大于上一路程则记录上一路程

end

track(count,:) = S1;%把当前的城市顺序记录下来

T0 = q * T0; %降温

end

%% VII. 优化过程迭代图

figure

plot(1:count,Obj)

xlabel('迭代次数')

ylabel('距离')

title('优化过程')

%% VIII. 绘制最优路径图

DrawPath(track(end,:),X)

%% IX. 输出最优解的路线和总距离

disp('最优解:')

S = track(end,:);

p = OutputPath(S);

disp(['总距离：',num2str(PathLength(D,S))]);

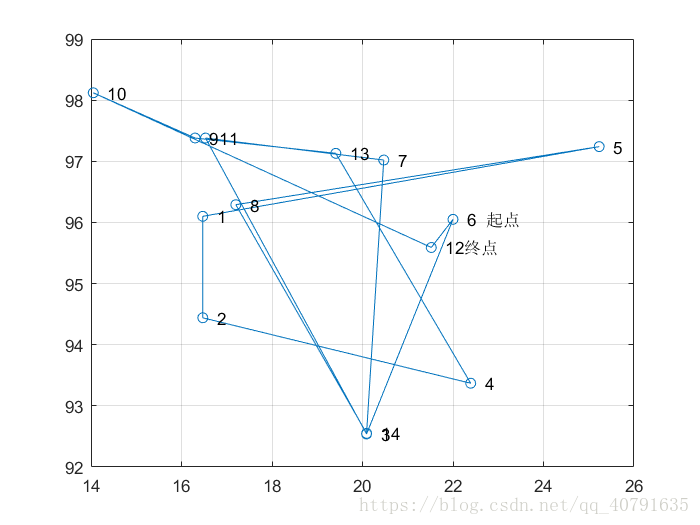
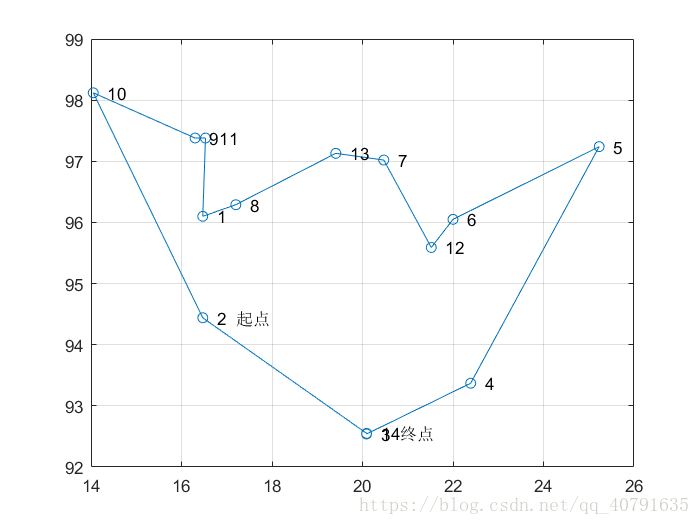
结果图片

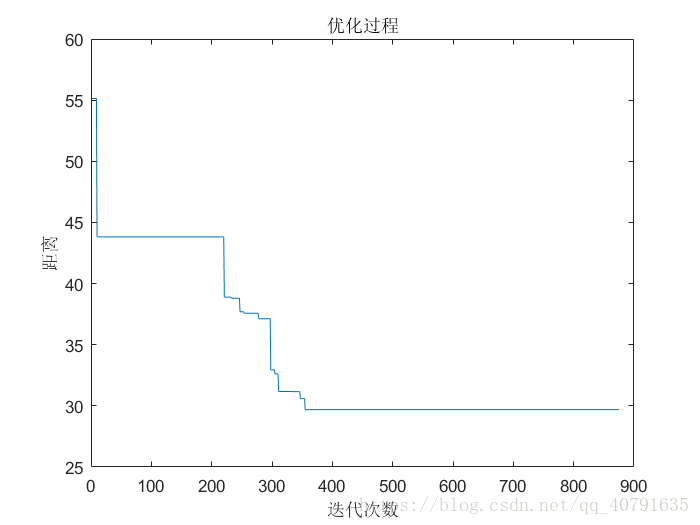
初始的排序：可见非常杂乱，距离也非常长。

最后的排序：可见距离已经得到了优化。

四、基本语法总结：

1、num2str 函数，其实是num to string,这个2是to的谐音，设计得很巧妙也容易看懂，恰好把num和str分开了。所有文本的显示都要把数字向string类型转换。

示例：num2str(x(maxIndex))把x矩阵中的第（maxindex）个变量变为string类型

2、text函数，在指定坐标插入文字。text就是文本的意思。

示例：text(x(minIndex), minVal, {[' X: ' num2str(x(minIndex))];[' Y: ' num2str(minVal)]})

前面两个是位置参数，后面“一个”是内容参数，它拿大括号括起来，

单引号前面不能带东西，要拿空格，逗号或者分号隔开，否则单引号会被看做和前面的字符一起是个整体。

示例：text(x(minIndex), minVal, {[' X: 'num2str(x(minIndex))]' Y: ' num2str(minVal)})在这个里面Y前面的引号就是错误的。

其次，在这个里面，X有中括号，Y没有，有没有中括号“表示在不在同一行”，没有中括号会自动分配到下一行。

最后' X: ' num2str(x(minIndex))这样写（只空了一个空格）

和' X: ' num2str(x(minIndex))这样写是没有区别的，在matlab里面，变量之间的空格再多和一个空格是没有区别的，但是变量之间至少要有一个空格（打逗号其实更直观）。文本里面空格数量上的差别要放到‘’字符串里面去体现。

size(X,1),返回矩阵X的行数；
size(X,2),返回矩阵X的列数；
N=size(X,2)，就是把矩阵X的列数赋值给N

4、对于一个矩阵x,x^2与x.^2（前面有一个点）是有区别的！

>> x=magic(3)

x =

     8     1     6
     3     5     7
     4     9     2

>> x.^2

ans =

    64     1    36
     9    25    49
    16    81     4

>> x^2

ans =

    91    67    67
    67    91    67
    67    67    91

>> x*x

ans =

    91    67    67
    67    91    67
    67    67    91

5、如何在矩阵A的某个位置插入一行

A=[ 1    12     7
     3      8       5
     4      3      6];
A=[A(1,:);[0    1      2];A(2:3,:)]

6、sum函数sum(x),输出x矩阵的列之和，但是如果x的矩阵只有一行，输出的是x的那一行的和。

sum(A(1:t,:),1) %对矩阵前1到t行按列求和

sum(A(1:t,:),2) %对矩阵前1到t行按行求和

b=sum(A,1) %对整个矩阵按列求和

b=sum(A,2) %对整个矩阵按行求和

c=sum(A(:)) %整个矩阵整体求和

Ceil 向上取整

floor 向下取整

Round 四舍五入

8、

solve([num2str(T0) '*(0.9)^x = ',num2str(Tend)])

%##这个solve函数是用来解方程的语法，非常重要。各个独立的字符串之间要有空格或者逗号。

9、随机函数randperm与randi

randperm:randperm返回一个从1-n的包含n个数的随机排列（每个数字只出现一次）——以行向量的形式

new = old( randperm( size(old,1) ) , : ); 打乱原来的数组的行序列，列序列没有改变，但是每一个列里面的元素的顺序变了。

randi:randi 生成均匀分布的伪随机整数(可能重复)

r = randi(imax)

返回一个介于1到imax的伪随机整数

r = randi(imax,n)

返回一个在[1,imax]范围内的n*n的伪随机整数矩阵

r = randi(imax,m,n)

返回一个在[1,imax]范围内的m*n的伪随机整数矩阵

r = randi(imax,[m,n])

同上，返回一个在[1,imax]范围内的的m*n的伪随机整数矩阵

r = randi(imax,m,n,p,...)

返回一个在[1,imax]范围内的m*n*p*...的伪随机整数矩阵

r = randi(imax,[m,n,p,...])

同上，返回一个在[1,imax]范围内的m*n*p*...的伪随机整数矩阵

r = randi(imax,size(A))

返回一个在[1,imax]范围内、和矩阵A一样大小的伪随机整数矩阵

r = randi([imin,imax],...)

返回一个在[imin,imax]范围内的伪随机整数

10、for i = 2:N

p = [p,'—>',num2str(R(i))];%把p变为一个字符串，中括号里面用逗号隔开，这是一个非常

end %巧妙的算法，不断在一个区间后面加字符。

11、disp函数即在命令行窗口打出所需要的显示的内容。

12、

Exploration 全局搜索

Exploitation 局部搜索

从根上面去想到底提升了哪个性能。

PS:模拟退火如果要求最大值，在目标函数面前加一个负号就行了。

找到一篇论文，里面对于遗传算法的重组过程有一个比较好的改进，那就是两个父代产生了两个子代，在这四个个体中选两个最优个体作为新的子代，而不是仅仅就单纯地选择产生的子代。这样产生的最优子代一定能原封不动地留下来，当然，还是失去了一些全局搜索的能力，通俗点说就是产生新个体，产生新组合，向补集探索的能力，新产生的一些子代肯定被淘汰，训练的时候更加“守旧”了，多样性变低了，你会说这些在当时比较的时候是劣势个体，应该要淘汰啊，但是劣势个体在当时是劣势的，说不定在以后的组合里面又凑成了一个很强势的个体呢？这都是有可能的。不过劣势个体还是能通过概率在选择的时候参与进来，只能说No free lunch定理吧。这个适用于群体优化，如果只想找最优解就没必要了，我觉得单独建一个数组保留最优个体，其余规则不变更好一些，找最优个体全局搜索能力不能削弱。

链接：https://wenku.baidu.com/view/82384501a6c30c2259019e23.html