数塔问题--动态规划问题--递推问题

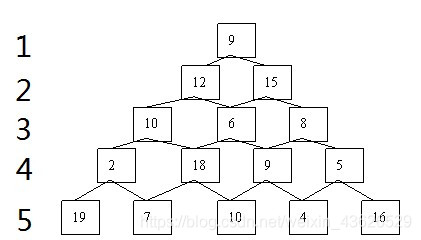
图是一个数塔，要求找出一条路径，使路径上的数组和最大

【Input】
第一行是一个整数N，表示数塔的高度，接下来用N行数字表示数塔，其中第i行有i个整数，且所有的整数均在区间[0，99]内

【Output】
输出可能得到的最大和

【Sample Input】
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

【Sample Output】
30

问题分析：
这道题目如果使用贪婪算法不能保证找到真正的最大和。
在用动态规划考虑数塔问题时可以自顶向下的分析，自底向上的计算。
从顶点出发时到底向左走还是向右走应取决于是从左走能取到最大值还是从右走能取到最大值，只要左右两道路径上的最大值求出来了才能作出决策。同样的道理下一层的走向又要取决于再下一层上的最大值是否已经求出才能决策。这样一层一层推下去，直到倒数第二层时就非常明了。
所以第一步对第五层的8个数据，做如下四次决策：
如果经过第四层2，则在第五层的19和7中肯定是19；
如果经过第四层18，则在第五层的7和10中肯定是10；
如果经过第四层9，则在第五层的10和4中肯定是10；
如果经过第四层5，则在第五层的4和16中肯定是16；
经过一次决策，问题降了一阶。5层数塔问题转换成4层数塔问题，如此循环决策…… 最后得到1阶的数塔问题。

#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int main(){
	int cnt[255][255];
	int n;
	cin >> n;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=i;j++){
			cin >> cnt[i][j];
		}
	} 
	for(int i=n-1;i>=1;i--){
		for(int j=1;j<=i;j++){
			if(cnt[i+1][j]>=cnt[i+1][j+1]) cnt[i][j]+=cnt[i+1][j];
			else cnt[i][j]+=cnt[i+1][j+1];
		}
	}
	cout << cnt[1][1];
	return 0;
} 

最后

以上就是魁梧紫菜为你收集整理的数塔问题--动态规划问题--递推问题的全部内容，希望文章能够帮你解决数塔问题--动态规划问题--递推问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。