动态规划（1）：数塔问题

题目

一些数字排成数塔的形状，其中第一层有一个数字，第二层有两个数字… 第n 层有n 个数字。现在要从第一层走到第n 层，每次只能走向下一层连接的两个数字中的一个，问：最后将路径上所有数字相加后得到的和最大是多少？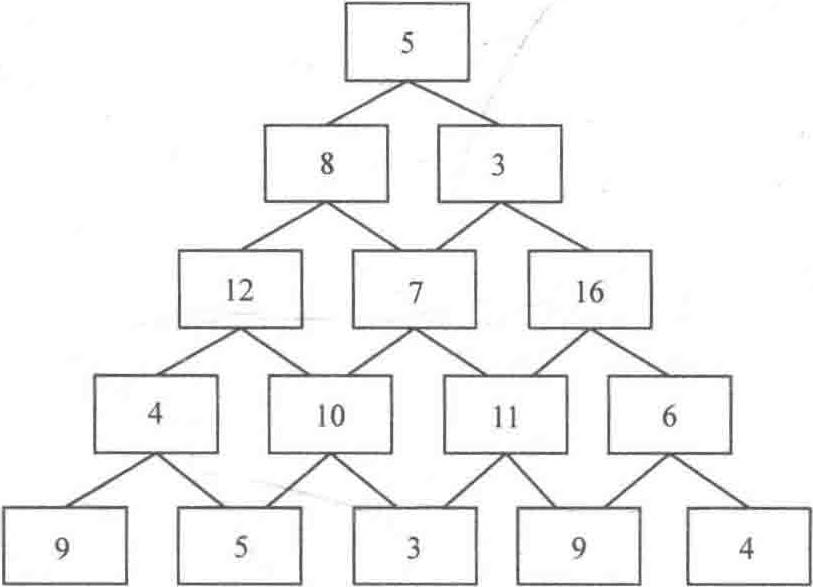

样例

5
5
8 3
12 7 16
4 10 11 6
9 5 3 9 4

题解

最优子结构：从5开始到结尾的最大和一定包含从8或者从3到结尾的最大和

重叠子问题：求8到结尾的，和从3到结尾的最大和都会用到从7到结尾的最大和

状态转移方程：
dp[n][j]=f[n][j];
dp[i][j]=max( dp[i+1][j],dp[i+1][j+1] )+f[i][j];

最优解：d[1][1]

C++代码

#include<cstdio>
#include"algorithm"
#include<iostream>
using namespace std;
#define N 100
int main(){
	int f[N][N],dp[N][N];//dp[i][j]表示从第i行j列的数开始到结尾的最大
	int n;
	cin>>n;
	//输入数塔
	for(int i=1;i<=n;i++)
			for(int j=1;j<=i;j++)
	{
		cin>>f[i][j];
	}
	//边界
	for(int j=1;j<=n;j++)
	{
		dp[n][j]=f[n][j];
	}
	
	for(int i=n-1;i>=1;i--)
			for(int j=1;j<=i;j++)
			{
				dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+f[i][j];
			}
    cout<<dp[1][1];
}

最后

以上就是称心含羞草为你收集整理的动态规划（1）：数塔问题的全部内容，希望文章能够帮你解决动态规划（1）：数塔问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。