数塔问题（动态规划

从数塔的顶层出发，在每一个结点可以选择向左走或向右走，一直走到底层，要求找出一条路径，使得路径上的数值和最大

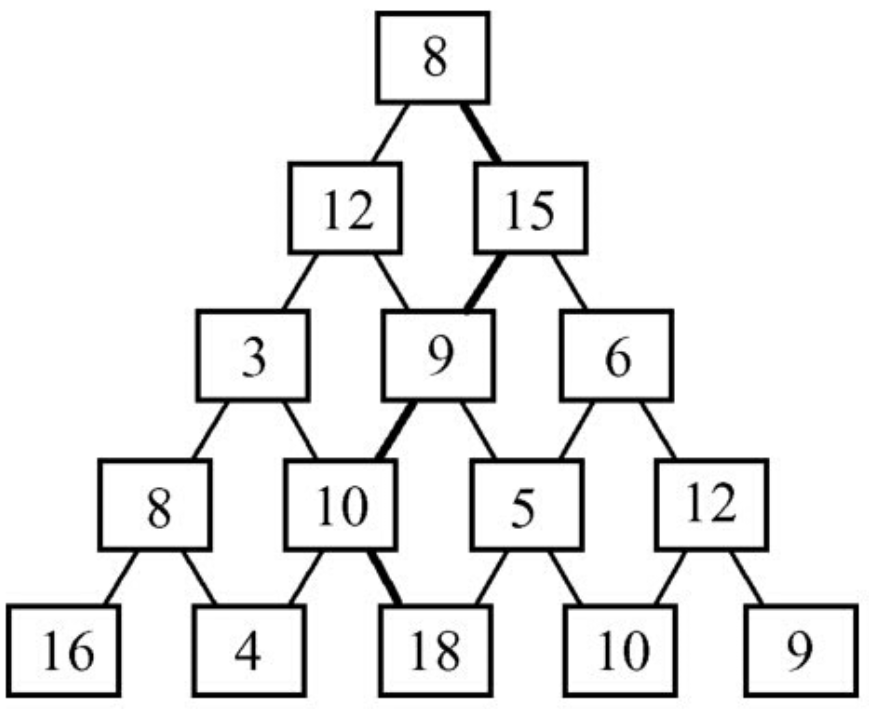
解决这个问题，可以将这个大问题分为若干个子问题求解，但是，子问题之间却往往不是独立的，是相互关联的，如果用分治法求解，这些子问题的重叠部分被重复计算多次，动态规划法将每个子问题求解一次并将其解保存在一个表格（通常采用数组）中，当需要再次解此子问题时，只是简单地通过查表获得该子问题的解，从而避免了大量重复计算。
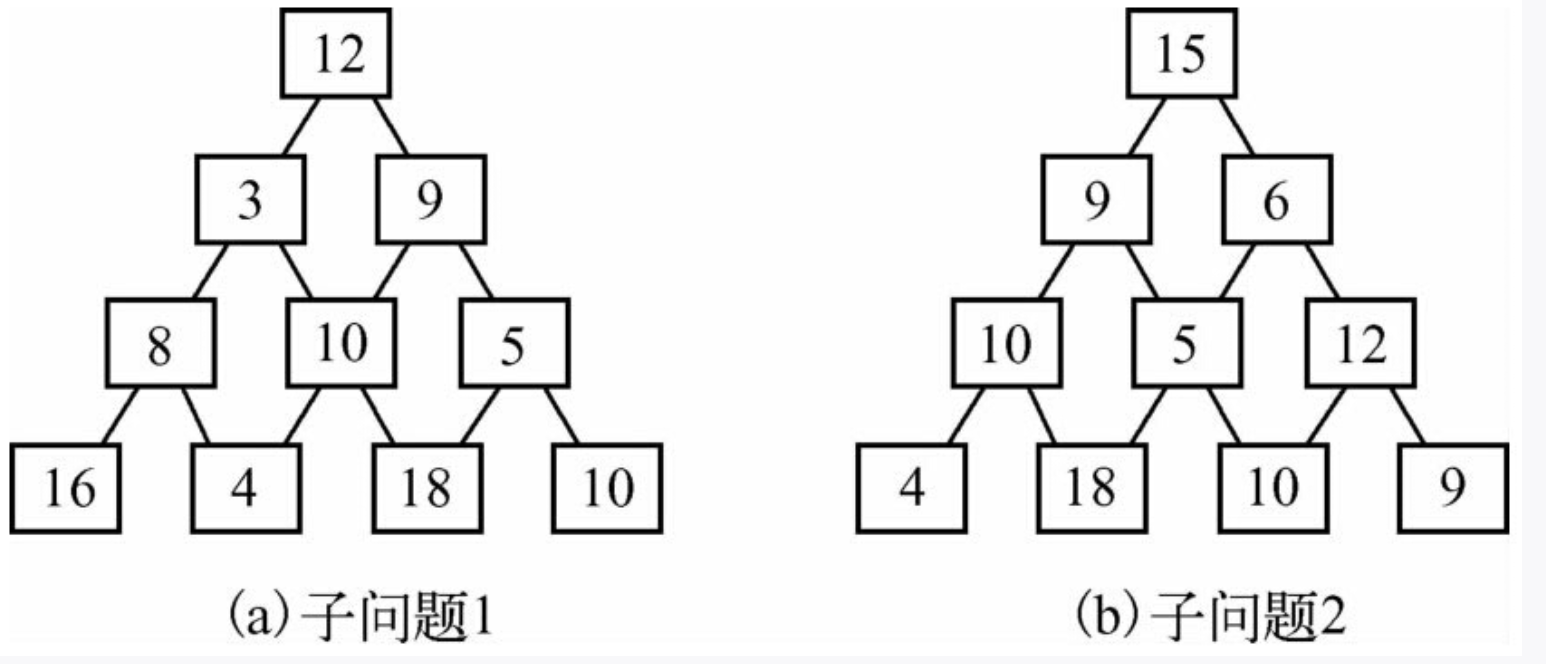
对于这道题目，我们可以将从第二层开始，分为两个子树，然后，比较这两个子树从底层找一条路径相加得到的最大值，不就可以知道是走右边还是左边了？
举个例子：
在(a)中 16比4大，所以选择16，同理，18比4大，选18，然后 18比10大，选10，然后将他们和上一层那个数相加，即16+8=24 ； 18+10=28； 18+5=23；（比较出结果后，把列的下表记录在 path[][]中，然后，然后逐渐往上，记录下表，最终得出路径的表格）

然后，两两比较，显然，28是最大的，所以选择10这条路 ，以此类推，最终回到顶层。

           #include<stdio.h>                        //使用库函数printf
            const int n=5;                              //假设数塔是5层
            int DataTorwer(int d[n][n]);              //函数声明，求解n层数塔
                                                       //以下是主函数
            int main()
            {
              int d[n][n]={{8},{12,15},{3,9,6},{8,10,5,12},{16,4,18,10,9}};
              printf("最大数值和为：%dn",DataTorwer(d)); //输出最大数值和
              return 0;  
			                                //将0返回操作系统，表明程序正常结束
            }
                                                       //以下是其他函数定义
            int DataTorwer(int d[n][n])                //求解数塔问题，数塔存储在数组d[n][n]中
            {
              int maxAdd[n][n]={0},path[n][n]={0};    //初始化
              int i,j;

              for(j=0;j<n;j++)                    //初始化底层决策结果
                  maxAdd[n-1][j]=d[n-1][j];
              for(i=n-2;i>=0;i--)                 //进行第i层的决策
                  for(j=0;j<=i;j++)               //填写addMax[i][j]，只填写下三角
                    if(maxAdd[i+1][j]>maxAdd[i+1][j+1])
                    {
                      maxAdd[i][j]=d[i][j]+maxAdd[i+1][j];
                      path[i][j]=j;                   //本次决策选择下标j的元素
                    }
                    else
                    {
                      maxAdd[i][j]=d[i][j]+maxAdd[i+1][j+1];
                      path[i][j]=j+1;                 //本次决策选择下标j+1的元素
                    }
              printf("路径为：%d",d[0][0]);      //输出顶层数字
              j=path[0][0];   //顶层决策是选择下一层列下标为path[0][0]的元素
              for(i=1;i<n;i++)
              {
                  printf("--＞%d",d[i][j]);
                  j=path[i][j];                       //本层决策是选择下一层列下标为path[i][j]的元素
              }
              printf("n");
              printf("路径表如下:n"); 
              for(int x= 0 ;x<5;x++)
              {
              	for(int y = 0 ; y<5;y++)
              	{
              	printf("%d    ",path[x][y]);
				  }
				  printf("n");
			  }
			    printf("n");
			      printf("n");
			    printf("原始的数塔可以表示为：n") ;
			   for( int x= 0 ;x<5;x++)
              {
              	for( int y = 0 ; y<5;y++)
              	{
              	printf("%d    ",d[x][y]);
				  }
				  printf("n");
			  }
              return maxAdd[0][0];                     //返回最大数值和，即最终的决策结果
            }

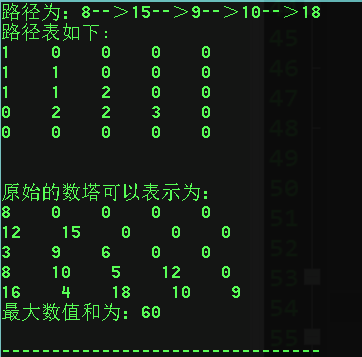
运行结果如图：

最后

以上就是虚幻小甜瓜为你收集整理的数塔问题（动态规划的全部内容，希望文章能够帮你解决数塔问题（动态规划所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。