针对本科和硕士应届生的算法面试题

维护一个前100大的最小堆，然后遍历一次O(nlogk)，显然当n很大时候效率也不是很高，

中位数即是排过序后的处于数组最中间的元素。 不考虑数组长度为偶数的情况。设集合元素个数为n。

简单的想了下：
思路1） 把无序数组排好序，取出中间的元素
            时间复杂度 采用普通的比较排序法 O(N*logN)
            如果采用非比较的计数排序等方法， 时间复杂度 O(N), 空间复杂度也是O(N).

思路2） 
          2.1）将前(n+1)/2个元素调整为一个小顶堆，
          2.2）对后续的每一个元素，和堆顶比较，如果小于等于堆顶，丢弃之，取下一个元素。 如果大于堆顶，用该元素取代堆顶，调整堆，取下一元素。重复2.2步           
          2.3）  当遍历完所有元素之后，堆顶即是中位数。

思路3） 熟话说，想让算法跑的更快，用分治！
            快速排序之所以得名"快排",绝非浪得虚名！因为快排就是一种分治排序法！
            同样，找中位数也可以用快排分治的思想。具体如下：
            任意挑一个元素，以改元素为支点，划分集合为两部分，如果左侧集合长度恰为 (n-1)/2，那么支点恰为中位数。如果左侧长度<(n-1)/2, 那么中位点在右侧，反之，中位数在左侧。 进入相应的一侧继续寻找中位点。
            这种方法很快，但是在最坏的情况下时间复杂度为O(N^2), 不过平均时间复杂度好像是O(N)。

思路4) 快排的方法存在不确定性,导致其最坏和最好的时候差别很大, 那么有没有一种确定性的方法呢? 答案是有的
            貌似算法导论里有讲到. 这里我就先不深究了, 可以参考如下的文章, 
            O(n)时间快速选择
            http://www.shadowxh.com/?p=598
            以及本文的别人的评论

引申一：
查找N个元素中的第K个小的元素（来自编程珠玑）
编程珠玑给出了一个时间复杂度O（N），的解决方案。该方案改编自快速排序。
经过快排的一次划分，
   1）如果左半部份的长度>K-1，那么这个元素就肯定在左半部份了
   2）如果左半部份的长度==K-1，那么当前划分元素就是结果了。
   3）如果。。。。。。。<K-1,那么这个元素就肯定在右半部分了。
  并且，该方法可以用尾递归实现。效率更高。

时间复杂度分析， 由于差不多每次都是把序列划分为一半。。。假设划分的元素做了随机优化，时间复杂度近似于
N+N/2+N/4.... = 2N*(1-2^-(logN)) 当N较大时 约等于 2N 也就是 O（N）。

看来，快速排需的用处可大着咧。。。

也用来查找可以N个元素中的前K个小的元素，前K个大的元素。。。。等等。

引申二：
查找N个元素中的第K个小的元素，假设内存受限，仅能容下K/4个元素。
分趟查找，
第一趟，用堆方法查找最小的K/4个小的元素，同时记录剩下的N-K/4个元素到外部文件。
第二趟，用堆方法从第一趟筛选出的N-K/4个元素中查找K/4个小的元素，同时记录剩下的N-K/2个元素到外部文件。
。。。
第四趟，用堆方法从第一趟筛选出的N-K/3个元素中查找K/4个小的元素，这是的第K/4小的元素即使所求。

不少朋友看到上面的答案之后，认为上述思路2的代码，没有处理全是负数的情况，当全是负数的情况时，我们可以让程序返回0，也可以让其返回最大的那个负数，下面便是前几日重写的，修改后的处理全是负数情况（返回最大的负数）的代码：

//copyright@ July
//July、updated，2011.05.25。
#include <iostream.h>
#define n 4           //多定义了一个变量

int maxsum(int a[n])  
//于此处，你能看到上述思路2代码（指针）的优势
{
    int max=a[0];       //全负情况，返回最大数
    int sum=0;
    for(int j=0;j<n;j++)
    {
        if(sum>=0)     //如果加上某个元素，sum>=0的话，就加
            sum+=a[j];
        else   
            sum=a[j];  //如果加上某个元素，sum<0了，就不加
        if(sum>max)
            max=sum;
    }
    return max;
}

int main()
{
    int a[]={-1,-2,-3,-4};
    cout<<maxsum(a)<<endl;
    return 0;
}

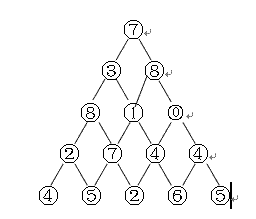
5、如图所示的数字三角形，从顶部出发，在每一结点可以选择向左走或得向右走，一直走到底层，要求找出一条路径，使路径上的值的和最大。给出算法的时间复杂度。

# include<cstdio>
# include<iostream>
# include<algorithm>
# include<cstring>
# include<string>
# include<cmath>
# include<queue>
# include<stack>
# include<set>
# include<map>

using namespace std;

# define inf 999999999
# define MAX 123

int a[MAX][MAX];

int main(void)
{
    int n;
    while ( cin>>n )
    {
        for ( int i = 1;i <= n;i++ )
        {
            for ( int j = 1;j <= i;j++ )
            {
                cin>>a[i][j];
            }
        }
        for ( int i = n-1;i >= 1;i-- )
        {
            for ( int j = 1;j <= i;j++ )
            {
                a[i][j] = max(a[i+1][j],a[i+1][j+1])+a[i][j];
            }
        }
        printf("%dn",a[1][1]);

    }

	return 0;
}

6、有一个很长二进制串，求出除以3的余数是多少，给出算法的时间复杂度。