动态规划--数塔问题

动态规划–数塔问题

今天学习了动态规划的数塔问题，老师给我们讲了三种方法。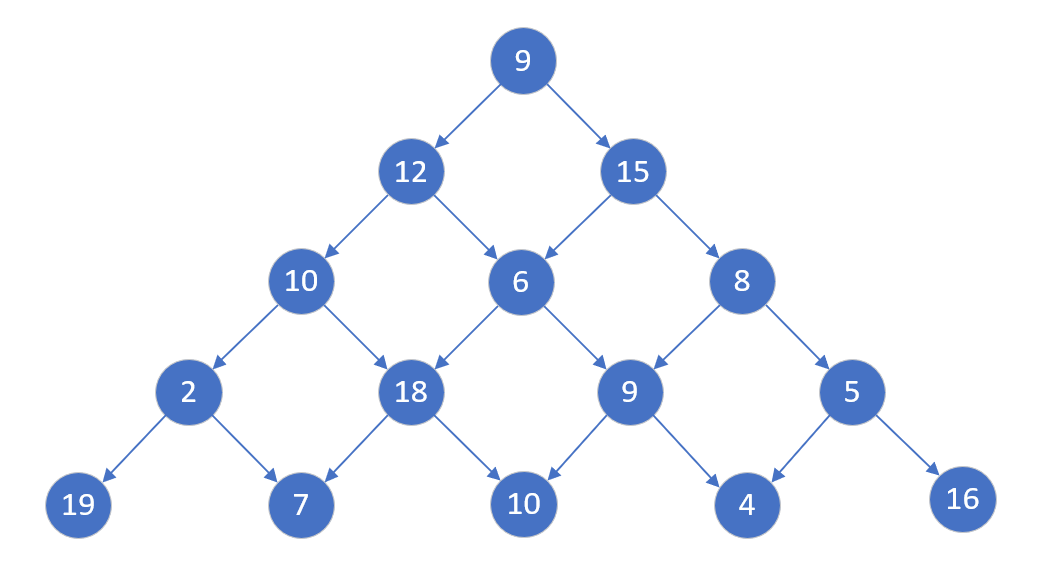
（1）第一种方法是原始的递归，就是从上往下看一个n层塔的最大路径问题可以转化为选出左右两个n-1层塔的最大路径问题的较大值，即：f(n)=max{ f(左,n-1), f(右,n-1) }，依次向下直到第n层。

左边n-1数塔问题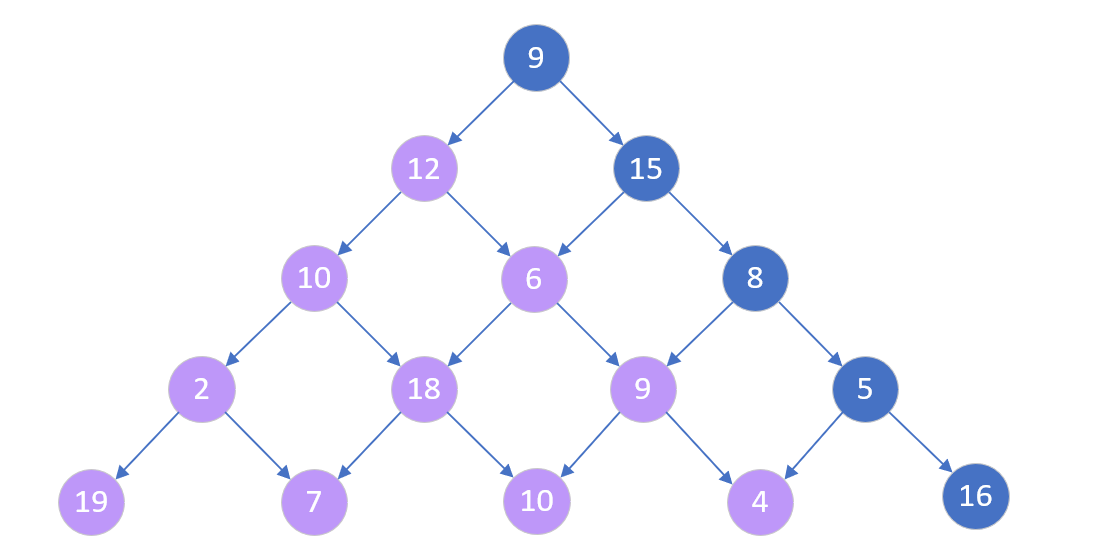

右边n-1数塔问题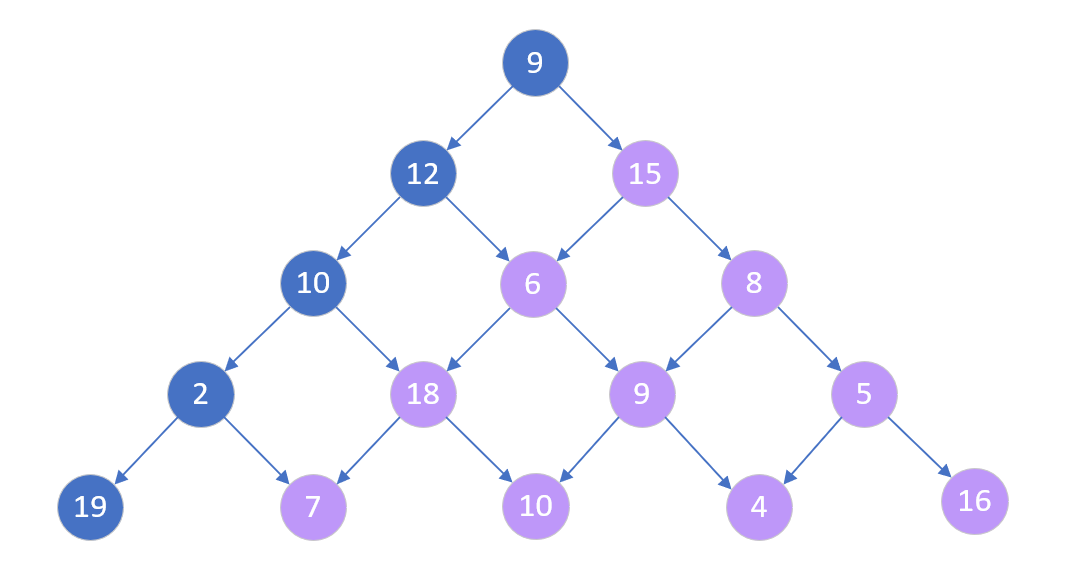

int f1(int i, int j){
	if(i < n-1)	
		return data[i][j] + max(f1(i+1,j),f1(i+1,j+1));
	else
		return data[i][j];
}

考虑到每次在计算是都会出现重复，因此有了方法二。

重复计算的区域

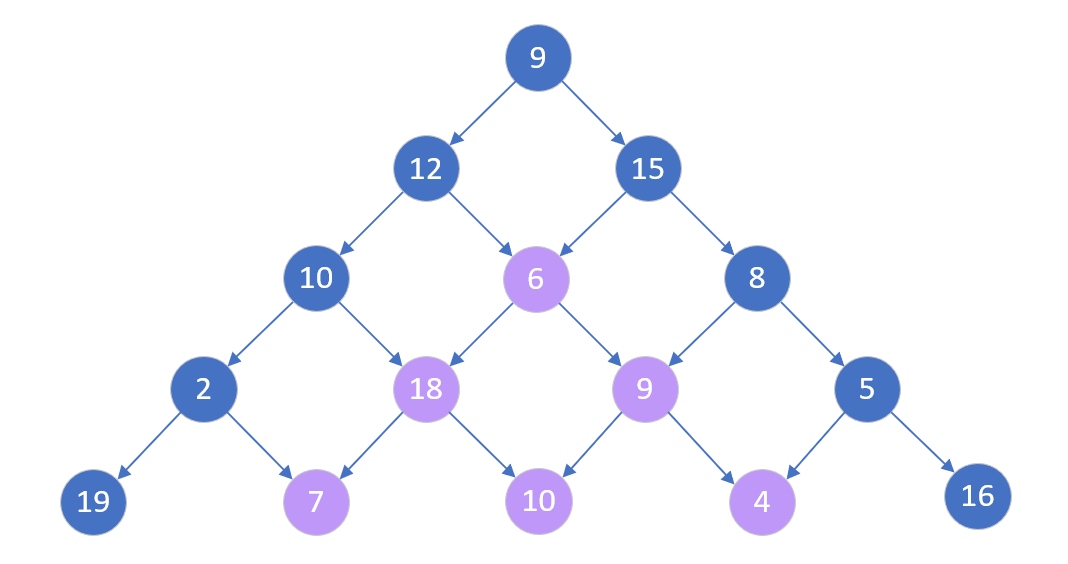
（2）第二种方法是对第一种方法的改进。把计算的结果放到一个数组里面就不会重复计算了。

int f2(int i,int j){
	if(i < n-1){
		if(d[i][j] == 0){
			d[i][j] = data[i][j] + max(f1(i+1,j),f1(i+1,j+1));
		}
		return d[i][j];
	}
	else
		return data[i][j];
	
}

（3）第三种方法没有用递归，从下往上考虑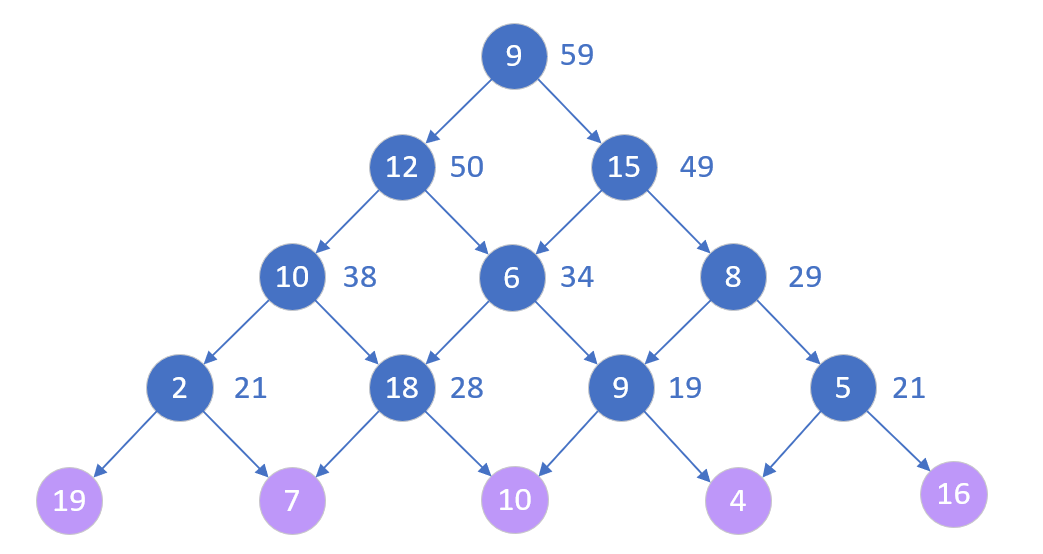

1. 一个底层为19、7、10、4、16的n层数塔问题就可以看成一个底层为21、28、19、21的n-1层数塔问题
2. 而对于每一层只需要考虑自己下面连接的左右两边哪个数大，就用自身的值加上这个较大值来更新自身的值。

for(i = n-2;i>=0;i--){
		for(j = 0;j<=i;j++){
			data[i][j] = data[i][j] + max(data[i+1][j],data[i+1][j+1]);
		}
	}
	printf("路径上值最大为：%d",data[0][0]);

总结：1、相比之下我更喜欢第三种方法，因为它既不用写递归函数也没有重复计算，而且不需要用两个数组。而且第一种方法只能得到最大值，但是无法得到最大路径。
2、要得到最大路径，需要从上往下推。

printf("最优路径为：%d",data[0][0]);
	j = 0;
	for(i = 1;i<n;i++){
		if(d[i][j]>d[i][j+1]){
			printf("-> %d",data[i][j]);
		}
		else{
			printf("-> %d",data[i][j+1]);
			j = j + 1;
		}		
	}

最优路径

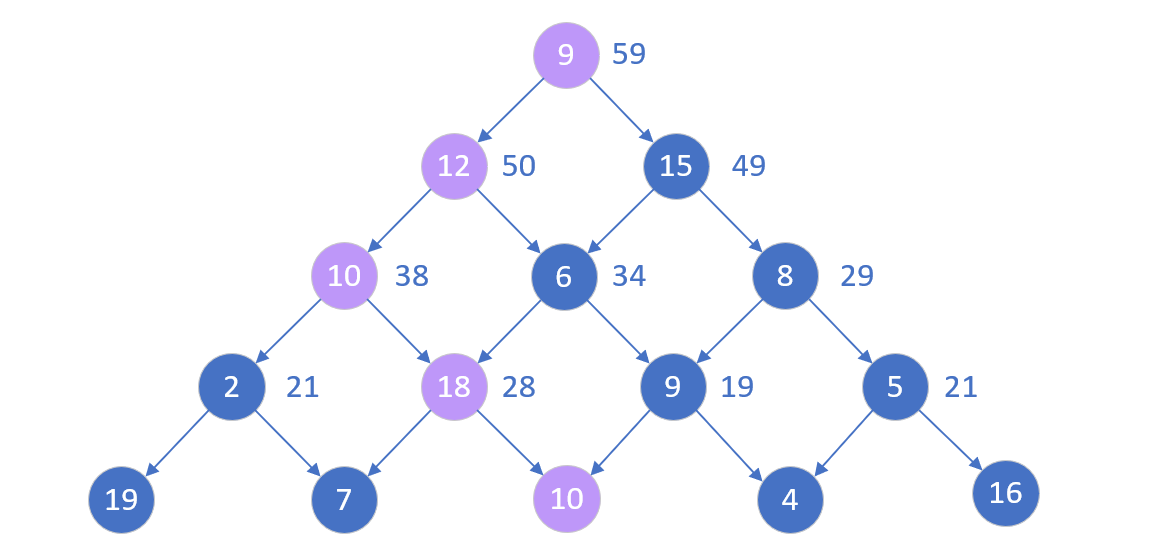
全部代码：（记得在用一种方法的时候把其他两个注释掉）

#include<stdio.h>
const int n = 5;
int data[n][n] = {0};
int d[n][n] = {0};
int max(int x,int y){
	if(x>y)	return x;
	else	return y;
}
int f1(int i, int j){
	if(i < n-1)		return data[i][j] + max(f1(i+1,j),f1(i+1,j+1));
	else	return data[i][j];
}

int f2(int i,int j){
	if(i < n-1){
		if(d[i][j] == 0){
			d[i][j] = data[i][j] + max(f1(i+1,j),f1(i+1,j+1));
		}
		return d[i][j];
	}
	else	return data[i][j];
	
}
int main(){
	int i,j;
	printf("请依次输入数塔各顶点的值：n"); 
	for(i = 0;i<n;i++){
		for(j = 0;j<=i;j++){
			scanf("%d",&data[i][j]);
		}
	}
	/方法一：从上到下，递归 
//	printf("路径上值最大为：%d",f1(0,0));
	/方法二：从上到下，加存储（备忘录法）
//	printf("路径上值最大为：%d",f2(0,0));
	/方法三：从下到上，阶段划分（填表法） 
	for(j = 0;j<n;j++){
		d[n-1][j] = data[n-1][j];
	}
	for(i = n-2;i>=0;i--){
		for(j = 0;j<=i;j++){
			d[i][j] = data[i][j] + max(d[i+1][j],d[i+1][j+1]);
		}
	}
	printf("路径上值最大为：%dn",d[0][0]);
	
	//得出最优路径
	
	printf("最优路径为：%d",data[0][0]);
	j = 0;
	for(i = 1;i<n;i++){
		if(d[i][j]>d[i][j+1]){
			printf("-> %d",data[i][j]);
		}
		else{
			printf("-> %d",data[i][j+1]);
			j = j + 1;
		}		
	}
	return 0;
} 

最后

以上就是愤怒小兔子为你收集整理的动态规划--数塔问题的全部内容，希望文章能够帮你解决动态规划--数塔问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。