概述
欧氏距离
上过初中的同学都知道，欧式距离是用来运算两个坐标之间的直线差值的方法，其公式为：
-
在一维坐标系内：
d = ∣ x 1 − x 2 ∣ d = |x_1-x_2| d=∣x1−x2∣ -
在二维坐标系内：
d = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 d = sqrt{(x_1-x_2)^2+(y_1-y_2)^2} d=(x1−x2)2+(y1−y2)2 -
在三维坐标系内：
d = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 + ( z 1 − z 2 ) 2 d = sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2} d=(x1−x2)2+(y1−y2)2+(z1−z2)2
曼哈顿距离
【曼哈顿距离的提出背景】
出租车几何或曼哈顿距离（Manhattan Distance）是由十九世纪的赫尔曼·闵可夫斯基所创词汇 ，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。
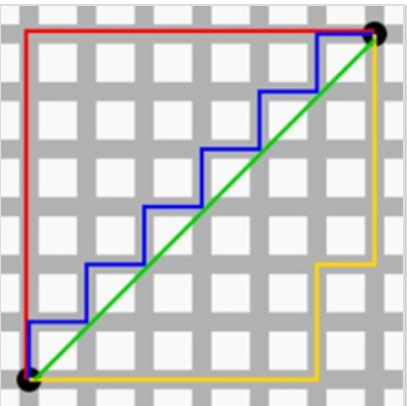
图 1 图中蓝线表示曼哈顿距离，绿线代表欧氏距离，红线和黄线代表和蓝线等效的曼哈顿距离
【曼哈顿距离的计算方法】
-
在一维坐标系内：
d = ∣ x 1 − x 2 ∣ d = |x_1-x_2| d=∣x1−x2∣ -
在二维坐标系内：
d = ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ d = |x_1-x_2|+|y_1-y_2| d=∣x1−x2∣+∣y1−y2∣ -
在三维坐标系内：
d = ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ + ∣ z 1 − z 2 ∣ d = |x_1-x_2|+|y_1-y_2|+|z_1-z_2| d=∣x1−x2∣+∣y1−y2∣+∣z1−z2∣
【曼哈顿网格的应用场景和意义】
曼哈顿距离示意图在早期的计算机图形学中，屏幕是由像素构成，是整数，点的坐标也一般是整数，原因是浮点运算很昂贵，很慢而且有误差，如果直接使用AB的欧氏距离(欧几里德距离：在二维和三维空间中的欧氏距离的就是两点之间的距离），则必须要进行浮点运算，如果使用AC和CB，则只要计算加减法即可，这就大大提高了运算速度，而且不管累计运算多少次，都不会有误差。
最后
以上就是超帅红牛为你收集整理的曼哈顿距离及其应用场景/曼哈顿距离与欧氏距离的不同欧氏距离曼哈顿距离的全部内容，希望文章能够帮你解决曼哈顿距离及其应用场景/曼哈顿距离与欧氏距离的不同欧氏距离曼哈顿距离所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复