原文:http://www.cnblogs.com/walccott/p/4957098.html
梯度下降与随机梯度下降
梯度下降法先随机给出参数的一组值,然后更新参数,使每次更新后的结构都能够让损失函数变小,最终达到最小即可。在梯度下降法中,目标函数其实可以看做是参数的函数,因为给出了样本输入和输出值后,目标函数就只剩下参数部分了,这时可以把参数看做是自变量,则目标函数变成参数的函数了。梯度下降每次都是更新每个参数,且每个参数更新的形式是一样的,即用前一次该参数的值减掉学习率和目标函数对该参数的偏导数(如果只有1个参数的话,就是导数),为什么要这样做呢?通过取不同点处的参数可以看出,这样做恰好可以使原来的目标函数值变低,因此符合我们的要求(即求函数的最小值)。即使当学习速率固定(但不能太大),梯度下降法也是可以收敛到一个局部最小点的,因为梯度值会越来越小,它和固定的学习率相乘后的积也会越来越小。在线性回归问题中我们就可以用梯度下降法来求回归方程中的参数。有时候该方法也称为批量梯度下降法,这里的批量指的是每一时候参数的更新使用到了所有的训练样本。
首先我们来定义输出误差,即对于任意一组权值向量,那它得到的输出和我们预想的输出之间的误差值。定义误差的方法很多,不同的误差计算方法可以得到不同的权值更新法则,这里我们先用这样的定义:
上面公式中D代表了所有的输入实例,或者说是样本,d代表了一个样本实例,od表示感知器的输出,td代表我们预想的输出。
这样,我们的目标就明确了,就是想找到一组权值让这个误差的值最小,显然我们用误差对权值求导将是一个很好的选择,导数的意义是提供了一个方向,沿着这个方向改变权值,将会让总的误差变大,更形象的叫它为梯度。
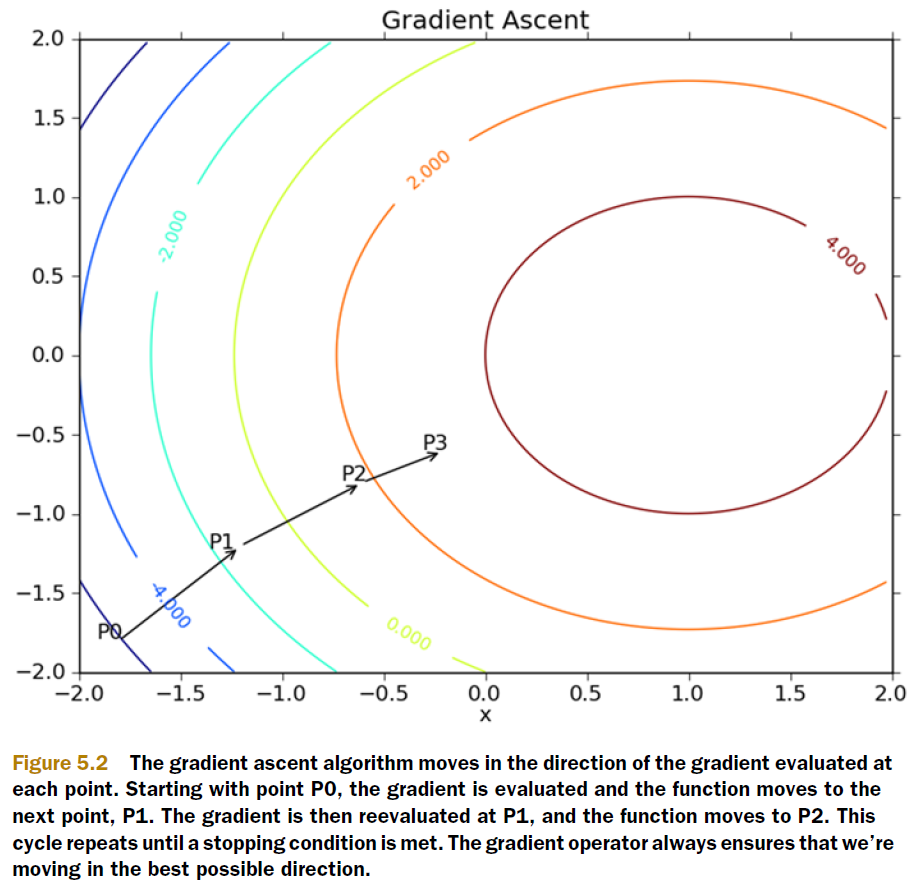
既然梯度确定了E最陡峭的上升的方向,那么梯度下降的训练法则是:
梯度上升和梯度下降其实是一个思想,上式中权值更新的+号改为-号也就是梯度上升了。梯度上升用来求函数的最大值,梯度下降求最小值。
这样每次移动的方向确定了,但每次移动的距离却不知道。这个可以由步长(也称学习率)来确定,记为α。这样权值调整可表示为:
关于学习率
如果学习速率过大,这每次迭代就有可能出现超调的现象,会在极值点两侧不断发散,最终损失函数的值是越变越大,而不是越来越小。在损失函数值——迭代次数的曲线图中,可以看到,该曲线是向上递增的。当然了,当学习速率过大时,还可能出现该曲线不断震荡的情形。如果学习速率太小,这该曲线下降得很慢,甚至在很多次迭代处曲线值保持不变。那到底该选什么值呢?这个一般是根据经验来选取的,比如从…0.0001,0.001,.0.01,0.1,1.0…这些参数中选,看那个参数使得损失值和迭代次数之间的函数曲线下降速度最快。有定步长和可变步长两种策略。
Feature Scaling
多变量
随机梯度下降
普通的梯度下降算法在更新回归系数时要遍历整个数据集,是一种批处理方法,这样训练数据特别忙庞大时,可能出现如下问题:
1)收敛过程可能非常慢;
2)如果误差曲面上有多个局极小值,那么不能保证这个过程会找到全局最小值。
为了解决上面的问题,实际中我们应用的是梯度下降的一种变体被称为随机梯度下降。
上面公式中的误差是针对于所有训练样本而得到的,而随机梯度下降的思想是根据每个单独的训练样本来更新权值,这样我们上面的梯度公式就变成了:
经过推导后,我们就可以得到最终的权值更新的公式:
有了上面权重的更新公式后,我们就可以通过输入大量的实例样本,来根据我们预期的结果不断地调整权值,从而最终得到一组权值使得我们的SIGMOID能够对一个新的样本输入得到正确的或无限接近的结果。
这里做一个对比
设代价函数为
批量梯度下降
参数更新为:
i是样本编号下标,j是样本维数下标,m为样例数目,n为特征数目。所以更新一个θj需要遍历整个样本集
随机梯度下降
参数更新为:
i是样本编号下标,j是样本维数下标,m为样例数目,n为特征数目。所以更新一个θj只需要一个样本就可以。
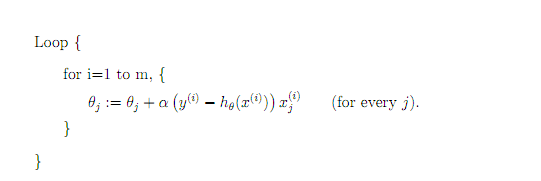
Batch Gradient Descent: You need to run over every training example before doing an update, which means that if you have a large dataset, you might spend much time on getting something that works.
Stochastic gradient descent, on the other hand, does updates every time it finds a training example, however, since it only uses one update, it may never converge, although you can still be pretty close to the minimum.
随机梯度下降的样本学习顺序可以这样来:
第一次打乱样本集D原来的顺序,得到D1,然后按顺序在D1上一个一个学习,所有样本学习完之后,再打乱D的顺序,得到D2,然后按顺序在D1上一个一个学习。。。
还有一种mini-batch gradient descent
普通梯度下降
这里的error和h是向量,m、n分别是样本数量、样本维数
- def gradAscent(dataMatIn, classLabels):
- dataMatrix = mat(dataMatIn) #convert to NumPy matrix
- labelMat = mat(classLabels).transpose() #convert to NumPy matrix
- m,n = shape(dataMatrix)
- alpha = 0.001
- maxCycles = 500
- weights = ones((n,1))
- for k in range(maxCycles): #heavy on matrix operations
- h = sigmoid(dataMatrix*weights) #matrix mult
- error = (labelMat - h) #vector subtraction
- weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
- return weights
- def stocGradAscent0(dataMatrix, classLabels):
- m,n = shape(dataMatrix)
- alpha = 0.01
- weights = ones(n) #initialize to all ones
- for i in range(m):
- h = sigmoid(sum(dataMatrix[i]*weights))
- error = classLabels[i] - h
- weights = weights + alpha * error * dataMatrix[i]
- return weights
改进的随机梯度下降,m、n分别是样本数量、样本维数
- def stocGradAscent1(dataMatrix, classLabels, numIter=150):
- m,n = shape(dataMatrix)
- weights = ones(n) #initialize to all ones
- for j in range(numIter):
- dataIndex = range(m)
- for i in range(m):
- alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not
- randIndex = int(random.uniform(0,len(dataIndex)))#随机选取样本
- h = sigmoid(sum(dataMatrix[randIndex]*weights))
- error = classLabels[randIndex] - h
- weights = weights + alpha * error * dataMatrix[randIndex]
- del(dataIndex[randIndex])#删除所选的样本
- return weights
下面是一些机器学习算法的随机梯度下降求解模型
与牛顿法的比较
梯度下降法是用来求函数值最小处的参数值,而牛顿法是用来求函数值为0处的参数值,这两者的目的初看是感觉有所不同,但是再仔细观察下牛顿法是求函数值为0时的情况,如果此时的函数是某个函数A的导数,则牛顿法也算是求函数A的最小值(当然也有可能是最大值)了,因此这两者方法目的还是具有相同性的。牛顿法的参数求解也可以用矢量的形式表示,表达式中有hession矩阵和一元导函数向量。
首先的不同之处在于梯度法中需要选择学习速率,而牛顿法不需要选择任何参数。第二个不同之处在于梯度法需要大量的迭代次数才能找到最小值,而牛顿法只需要少量的次数便可完成。但是梯度法中的每一次迭代的代价要小,其复杂度为O(n),而牛顿法的每一次迭代的代价要大,为O(n^3)。因此当特征的数量n比较小时适合选择牛顿法,当特征数n比较大时,最好选梯度法。这里的大小以n等于1000为界来计算。
总结
梯度下降与随机梯度下降是很多机器学习算法求解的基石,可以说是非常重要的。要求弄懂其中的数学原理,随手推导出公式,并能应用。
http://www.cnblogs.com/murongxixi/p/3467365.html
http://www.cnblogs.com/murongxixi/p/4254788.html
Stochastic Gradient Descent Training for L1-regularized Log-linear Models with Cumulative Penalty
最后
以上就是激情小懒虫最近收集整理的关于机器学习--神经网络算法系列--梯度下降与随机梯度下降算法的全部内容,更多相关机器学习--神经网络算法系列--梯度下降与随机梯度下降算法内容请搜索靠谱客的其他文章。
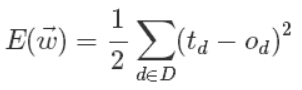
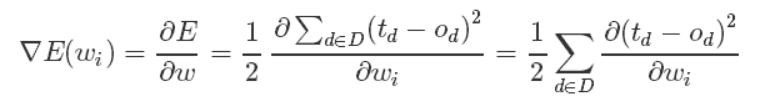

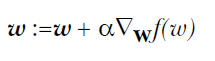
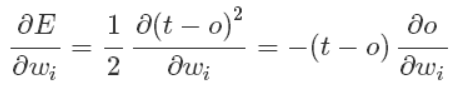
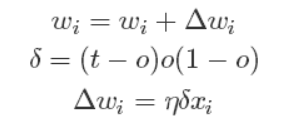
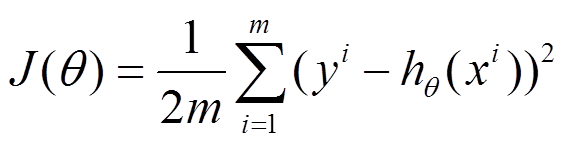
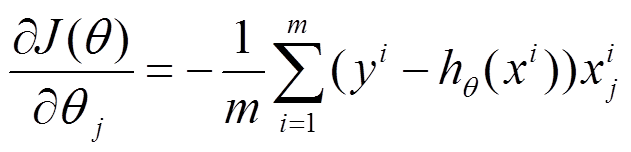
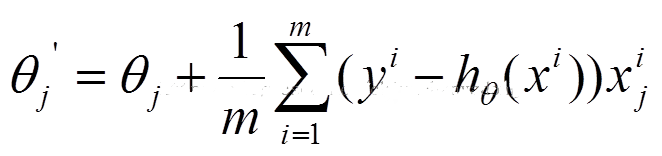
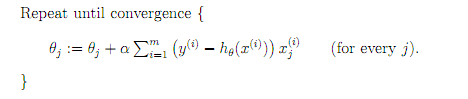
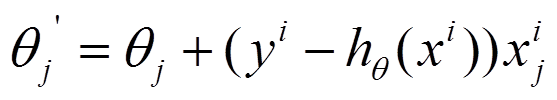









发表评论 取消回复