HDU1054Strategic Game(最小顶点覆盖数)

我们来先了解一下什么是最小顶点覆盖；

图G的顶点覆盖是一个顶点集合V，使得G中的每一条边都接触V中的至少一个顶点。我们称集合V覆盖了G的边。最小顶点覆盖是用最少的顶点来覆盖所有的边。顶点覆盖数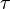是最小顶点覆盖的大小。

相应地，图G的边覆盖是一个边集合E，使得G中的每一个顶点都接触E中的至少一条边。

如果只说覆盖，则通常是指顶点覆盖，而不是边覆盖。

求二分图最大匹配可以用最大流(Maximal Flow)或者匈牙利算法(Hungarian Algorithm)

所以下面介绍主要一下匈牙利算法：

匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。匈牙利算法是基于Hall定理中充分性证明的思想，它是部图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。

题解：可以用匈牙利算法求解;用stl模版中的向量容器存放双向邻接表；

注意：1.本题中编号是从0开始；所以ret[]应初始化为-1；

2：向量要清零；

代码实现:

#include<stdio.h>
#include<cstring>
#include<vector>
using namespace std;
#pragma comment(linker,"/STACK:102400000,102400000")
#define MAX   1505
int visit[MAX];//标记节点是否被访问过；
int ret[MAX];//标记n个节点的增广节点的编号
vector<int>map[MAX];//用stl模版中的向量存放邻接表
int find(int cur )//找增广路径
{
     for(int i=0;i<map[cur].size();i++)
     {
          int j=map[cur][i];
          if(!visit[j])//若j与cur相邻，且没有被标记
          {
               visit[j]=1;
               if(ret[j]==-1||find(ret[j]))//如果j未在前一个匹配M中，或者，j在匹配M中，但从j相邻的节点出发可以找到增广路
               {
                    ret[j]=cur;//则把cur放到匹配M中；
                    return 1;
               }
          }
     }
     return 0;
}
int main()
{
  // freopen("input.txt","r",stdin);
     int n,x,m,y;
     while(scanf("%d",&n)!=EOF)
     {
          for(int i=0;i<n;i++)map[i].clear();//注意要清零；
          for(int i=0;i<n;i++)
          {
               scanf("%d:(%d)",&x,&m);
               for(int j=0;j<m;j++)
               {
                    scanf("%d",&y);
                    map[x].push_back(y);//用向量存放双向邻接表
                    map[y].push_back(x);
               }
          }
          int sum=0;
          memset(ret,-1,sizeof(ret));//因为节点从0开始，所以要赋值为-1；
          for(int i=0;i<n;i++)//
          {
               memset(visit,0,sizeof(visit));
               sum+=find(i);//若有增广路，匹配数则加一
          }
          printf("%dn",sum/2);//最小顶点覆盖 == 最大匹配（双向图）/2；
     }
   return 0;
}

最后

以上就是斯文小霸王为你收集整理的HDU1054Strategic Game(最小顶点覆盖数)的全部内容，希望文章能够帮你解决HDU1054Strategic Game(最小顶点覆盖数)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。