Strategic game
| Time Limit: 2000MS | Memory Limit: 10000K | |
| Total Submissions: 6722 | Accepted: 3095 |
Description
Bob enjoys playing computer games, especially strategic games, but sometimes he cannot find the solution fast enough and then he is very sad. Now he has the following problem. He must defend a medieval city, the roads of which form a tree. He has to put the minimum number of soldiers on the nodes so that they can observe all the edges. Can you help him?
Your program should find the minimum number of soldiers that Bob has to put for a given tree.
For example for the tree:
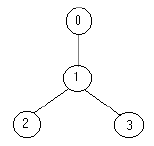
the solution is one soldier ( at the node 1).
Your program should find the minimum number of soldiers that Bob has to put for a given tree.
For example for the tree:

the solution is one soldier ( at the node 1).
Input
The input contains several data sets in text format. Each data set represents a tree with the following description:
The node identifiers are integer numbers between 0 and n-1, for n nodes (0 < n <= 1500);the number_of_roads in each line of input will no more than 10. Every edge appears only once in the input data.
- the number of nodes
- the description of each node in the following format
node_identifier:(number_of_roads) node_identifier1 node_identifier2 ... node_identifiernumber_of_roads
or
node_identifier:(0)
The node identifiers are integer numbers between 0 and n-1, for n nodes (0 < n <= 1500);the number_of_roads in each line of input will no more than 10. Every edge appears only once in the input data.
Output
The output should be printed on the standard output. For each given input data set, print one integer number in a single line that gives the result (the minimum number of soldiers). An example is given in the following:
Sample Input
4 0:(1) 1 1:(2) 2 3 2:(0) 3:(0) 5 3:(3) 1 4 2 1:(1) 0 2:(0) 0:(0) 4:(0)
Sample Output
1 2
题目大意:
一棵树,要放置哨兵,要求最少放置多少哨兵能监视到所有的结点。
解题思路:放置哨兵无非两种情况,要嘛放,要嘛不放,我们可以用dp[i][1]来表示第i个结点放置哨兵,dp[i][0]来表示第i个结点不放置哨兵,我们可以从上往下,从左往右来遍历树,所以这就用到了树形DP的知识,我们很容易知道,如果父亲结点没放哨兵,那么子结点肯定要放置哨兵,如果父亲放置了哨兵,那么子结点可以考虑放或者不放。所以很容易写出状态转移方程dp[v][1] += min(dp[u][1],dp[u][0]),dp[v][0] += dp[u][1],由于子结点可能有多个,我们要依次从左到右遍历所以我们必须开一个brother来存放它前一个兄弟结点,然后只要DFS递归的来从上往下遍历就可以得解了。
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 1505;
bool father[maxn]; //纵向遍历
int brother[maxn]; //横向遍历,因为有多个分支
int son[maxn]; //储存儿子结点
int dp[maxn][2]; //选择放还是不放
int m;
void tree(int root)
{
dp[root][0] = 0;
dp[root][1] = 1;
int f = son[root]; //求子节点
while(f != -1) //也就是还有子节点,横向继续遍历
{
tree(f); //纵向遍历
dp[root][1] += min(dp[f][0],dp[f][1]); //父亲放了,儿子可以放,也可以不放
dp[root][0] += dp[f][1]; //不过父亲不放,儿子就要放
f = brother[f]; //切换到下一个兄弟结点,横向遍历
}
}
int main()
{
int i,j;
int cnt;
//freopen("111","r",stdin);
while(cin>>m)
{
int num,num1;
int res;
int root;
memset(son,-1,sizeof(son));
memset(father,false,sizeof(father));
for(i=0;i<m;i++)
{
scanf("%d:(%d)",&num,&cnt);
for(j=0;j<cnt;j++)
{
cin>>num1;
brother[num1] = son[num]; //同一个父节点的上一个兄弟
son[num] = num1; //num的儿子是num1
father[num1] = true; //num1是有父亲的,为下面找根结点做准备
}
}
for(i=0;i<m;i++)
{
if(!father[i]) //如果没有父亲就可以做为根结点
{
root = i;
break;
}
}
tree(root);
res = min(dp[root][1],dp[root][0]);
cout<<res<<endl;
}
return 0;
}
最后
以上就是留胡子学姐最近收集整理的关于POJ1463 Strategic game(树形DP)Strategic game的全部内容,更多相关POJ1463内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。



![[Codeforces VK Cup 2016 - Round 2][矩阵树定理][高斯消元][骗(满)分]G. Little Artem and Graph](https://www.shuijiaxian.com/files_image/reation/bcimg1.png)




发表评论 取消回复