dp专题

66 阅读 0 评论 44 点赞

我是靠谱客的博主淡淡白开水，最近开发中收集的这篇文章主要介绍dp专题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

字符串类DP问题

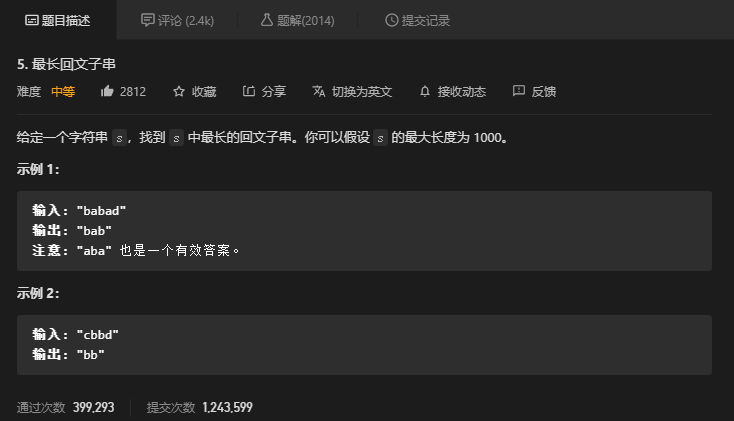
在这里插入图片描述

字符串类dp问题，一般是用一个二维数组表示dp[i][j]通常表示字符串 i位置到字符串 j位置需要做的哪些工作，亦或是从字符串1 i位置变换到字符串2的j位置，需要做的工作，这个需要了解一下。

class Solution {
    public String longestPalindrome(String s) {
        int len = s.length();
        if(len == 0) return s;
        char[] ch = s.toCharArray();
        boolean[][] dp = new boolean[len][len];
        int maxlen = 1;
        int start = 0;
        for(int i = 0; i<len; i++) dp[i][i] = true;
        for(int i = 1; i<len; i++){
            for(int j = 0; j<i; j++){
                if(ch[i] != ch[j]) dp[j][i] = false;
                else{
                    if(i-j < 3) dp[j][i] = true; // i-1 - (j+1) < 1 表示边界情况
                    else dp[j][i] = dp[j+1][i-1];
                }
                if(dp[j][i] && i-j+1 > maxlen){
                    maxlen = i-j+1;
                    start = j;
                }
            }
        }
        return s.substring(start, start+maxlen);
    }
}

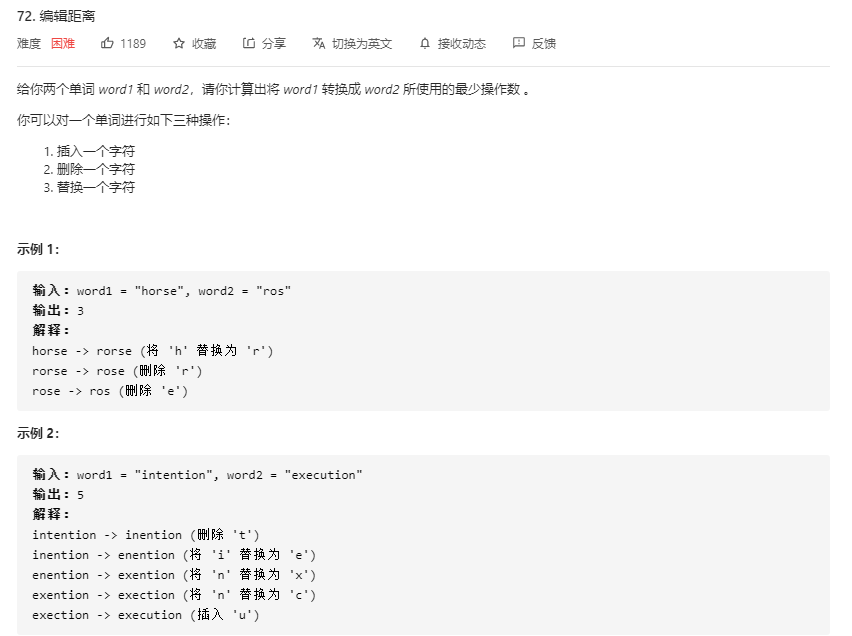
在这里插入图片描述

对“dp[i-1][j-1] 表示替换操作，dp[i-1][j] 表示删除操作，dp[i][j-1] 表示插入操作。”的补充理解：
以 word1 为 “horse”，word2 为 “ros”，且 dp[5][3] 为例，即要将 word1的前 5 个字符转换为 word2的前 3 个字符，也就是将 horse 转换为 ros，因此有：
(1) dp[i-1][j-1]，即先将 word1 的前 4 个字符 hors 转换为 word2 的前 2 个字符 ro，然后将第五个字符 word1[4]（因为下标基数以 0 开始）由 e 替换为 s（即替换为 word2 的第三个字符，word2[2]）
(2) dp[i][j-1]，即先将 word1 的前 5 个字符 horse 转换为 word2 的前 2 个字符 ro，然后在末尾补充一个 s，即插入操作
(3) dp[i-1][j]，即先将 word1 的前 4 个字符 hors 转换为 word2 的前 3 个字符 ros，然后删除 word1 的第 5 个字符

class Solution {
    public int minDistance(String word1, String word2) {
        int len1 = word1.length();
        int len2 = word2.length();
        if(len1 * len2 == 0) return len1 == 0 ? len2: len1;
        int[][] dp = new int[len1+1][len2+1];   // 表示word1的 0~i  变换到 word2 的 0~j 需要的步数
        for(int i = 1; i<=len1; i++) dp[i][0] = i;  // 删除
        for(int i = 1; i<=len2; i++) dp[0][i] = i;	// 插入
        
        for(int i = 1; i<=len1; i++){
            for(int j = 1; j<=len2; j++){
                if(word1.charAt(i-1) == word2.charAt(j-1)) dp[i][j] = dp[i-1][j-1];
                else{
                    // 替换 删除 插入  选 最小操作
                    dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1;
                }
            }
        }
        return dp[len1][len2];
    }
    public int min(int a, int b, int c){
        a = Math.min(a,b);
        return Math.min(a,c);
    }
}

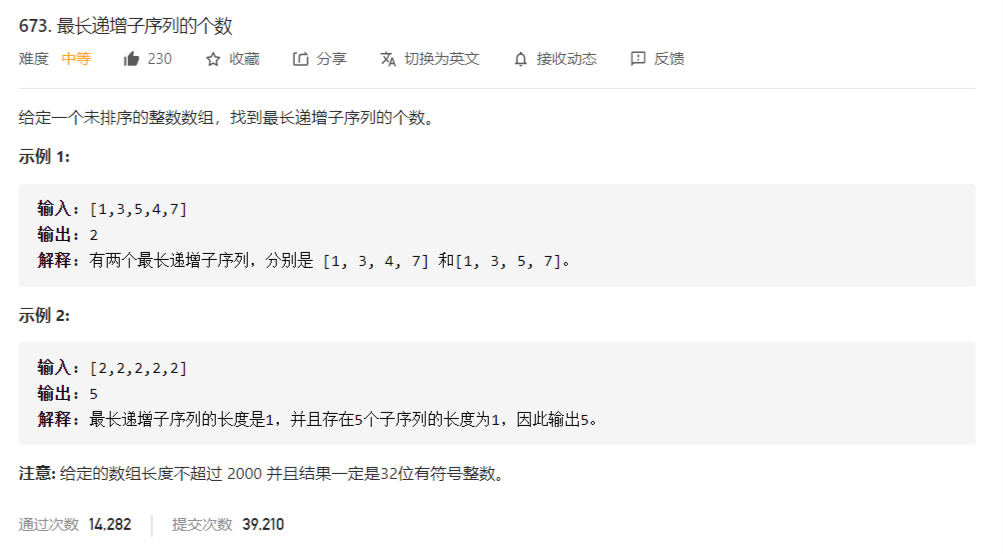
这题是在之前最长递增子序列的基础上进一步加大难度，在字节微软多个面试中考察到这个问题，需要理解并进行消化

在这里插入图片描述

 public int findNumberOfLIS(int[] nums) {
        if (nums == null || nums.length == 0) return 0;
        int n = nums.length;
        int[] dp = new int[n];
        int[] counter = new int[n];
        Arrays.fill(dp, 1);
        Arrays.fill(counter, 1);
        int max = 0;
        for (int i = 0; i ＜ n; i++) {
            for (int j = 0; j ＜ i; j++) {
                if (nums[i] ＞ nums[j]) {
                    if (dp[j] + 1 ＞ dp[i]) {
                        dp[i] = dp[j] + 1;
                        counter[i] = counter[j];
                    } else if (dp[j] + 1 == dp[i]) {
                        counter[i] += counter[j];
                    }
                }
            }
            max = Math.max(max, dp[i]);
        }
        int res = 0;
        for (int i = 0; i ＜ n; i++) {
            if (dp[i] == max) res += counter[i];
        }
        return res;
    }

作者：a-fei-8
链接：https://leetcode-cn.com/problems/number-of-longest-increasing-subsequence/solution/dong-tai-gui-hua-jie-zui-chang-zi-xu-lie-zi-chua-4/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

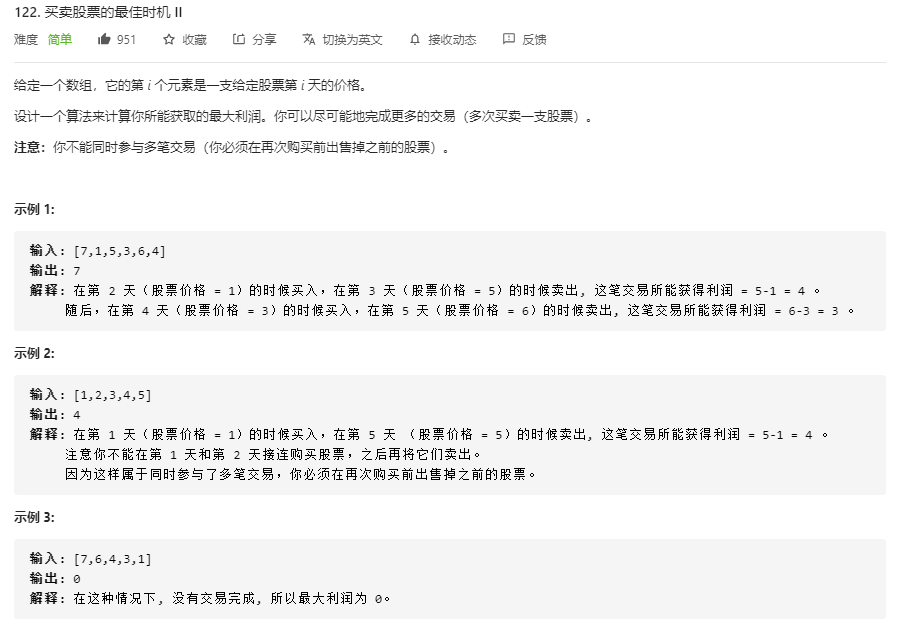
股票问题专场

在这里插入图片描述

class Solution {
    public int maxProfit(int[] prices) {
        int len = prices.length;
        if(len == 0) return 0;
        int[][]dp = new int[len][2];  // dp[i][0] 表示持有钱，dp[i][1] 表示持有股票
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        for(int i = 1; i<len; i++){
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);  // 上一阶段没有买留下的钱，和 这一阶段卖了留下的钱的最大值
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]); // 上一阶段的钱买了这阶段买了股票，上一阶段的钱，这阶段不买不卖 两者最大值
        }
        return dp[len-1][0];
    }
}

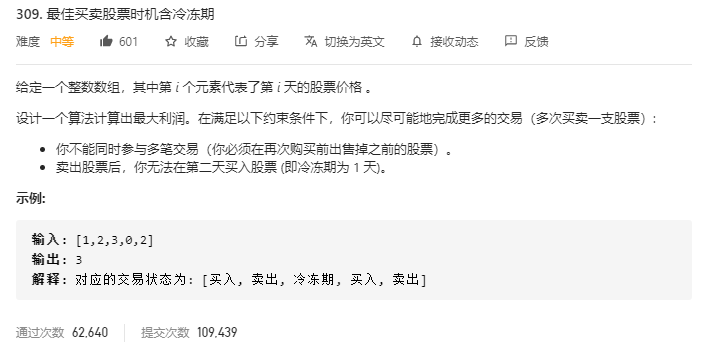
在这里插入图片描述

class Solution {
    public int maxProfit(int[] prices) {
        int len = prices.length;
        if(len == 0 || len == 1) return 0;
        int[][] dp = new int[len][3];
        /**
            0 表示：今天 不是 卖出了股票的不持股状态；
            1 表示：持股；
            2 表示：今天由于卖出了股票的不持股状态；
        */
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        dp[0][2] = 0;
        for(int i = 1; i<len; i++){
           dp[i][0] = Math.max(dp[i-1][0], dp[i-1][2]);
           dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0]-prices[i]);
           dp[i][2] = dp[i-1][1] + prices[i];
        }
        return Math.max(dp[len-1][0],dp[len-1][2]);
    }
}

dp[i][0] 非卖出股票的不持股状态可以由昨天本来不持股和昨天卖出股票不持股转化
dp[i][1] 持股状态可以由昨天持股和昨天不是卖出股票持股转化
dp[i][2] 只能由昨天买入股票转化，也就是昨天买进，今天卖出

在这里插入图片描述

class Solution {
    public int maxProfit(int[] prices, int fee) {
        int len = prices.length;
        if(len == 0) return 0;
        int[][] dp = new int[len][2]; // dp[i][0] 持有钱  dp[i][1] 持有 股票
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        for(int i = 1; i<len; i++){
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i] - fee);
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]);
        }
        return dp[len-1][0];
    }
}