相机几何学——相机投影矩阵（ Camera Projection Matrix）

相机投影矩阵为P，是MTMC任务中每个标定好的摄像机所配备的参数。总是忘记关于它的基本性质，现在写在这里

1. P矩阵的维度是3*4。

2. 相机成像过程可以描述为x=PX，其中X是一个4*1的向量：（X，Y，Z，1）T。

3. 左侧的x是成像后的像素点坐标（x,y,1）。

4. 成像过程：3*1 = 3*4   *   4*1。

P矩阵的内部目前还没有探究，但是已经了解到P的构成，P中包含旋转、平移矩阵，包含与世界坐标系的关系。（盗的柳桢的图hhh）
 

最近需要对EPFL的WildTrack数据集进行探究，第一步就是要明确相机标定的参数含义，将其使用起来。此数据集给定了K矩阵（3x3）、R参数（1x3）、T参数（1x3）。明确了这些参数后就可以通过公式计算投影矩阵。

要注意此处的R是rx、ry、rz（三个弧度值）通过三角函数运算来得到的，这三个弧度值不能直接用。在计算R的过程中有很多的版本，最后试来试去都不行，最后还是通过OpenCV自带的Rodrigus函数来将rx、ry、rz映射为R。

还有一点需要明确：下图公式中，K是3x4，RT是4x4，乘到一起是P（3x4）。实际也可以去掉底部的增广行，K是3x3，RT是3x4，乘到一起依然是P（3x4）。

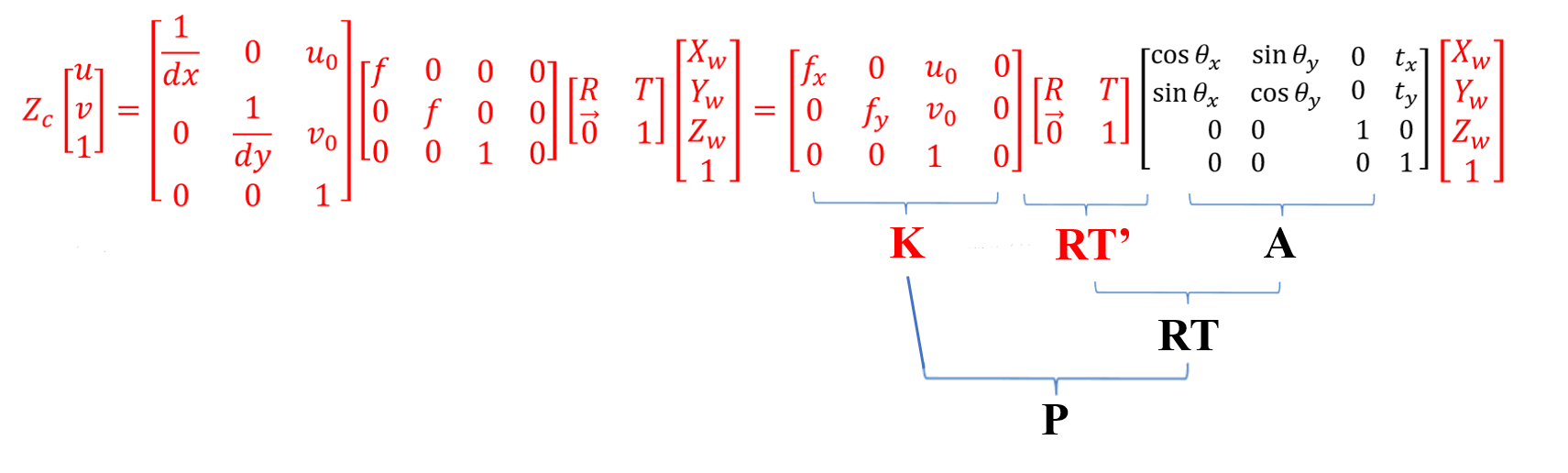
注意：

当使用x=P*X进行投影时，得到的x是3*1维，此时最后一位不一定是1，一定要进行归一化，即x中的值全部除以最后一位。此时的x和y才能做为图像上的点。

points_8 = Get_3D_rect(x, y, rect)    # points_8含有8个3D点，维度是4*8的array
img_points_8 = np.matmul(Ps[cam], points_8)    # 3*4的P矩阵和点进行相乘
img_points_8 = img_points_8/img_points_8[2,:]	# homogeneous进行归一化，之后可以在image上绘制

最后

以上就是含蓄火龙果为你收集整理的相机几何学——相机投影矩阵（ Camera Projection Matrix）的全部内容，希望文章能够帮你解决相机几何学——相机投影矩阵（ Camera Projection Matrix）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。