>>>文章索引<<<

相机标定（一）-原理及内参、外参
相机标定（二）-畸变校正，张正友标定法
相机标定（三）-相机成像模型

1 人眼&相机结构

1.1 类比

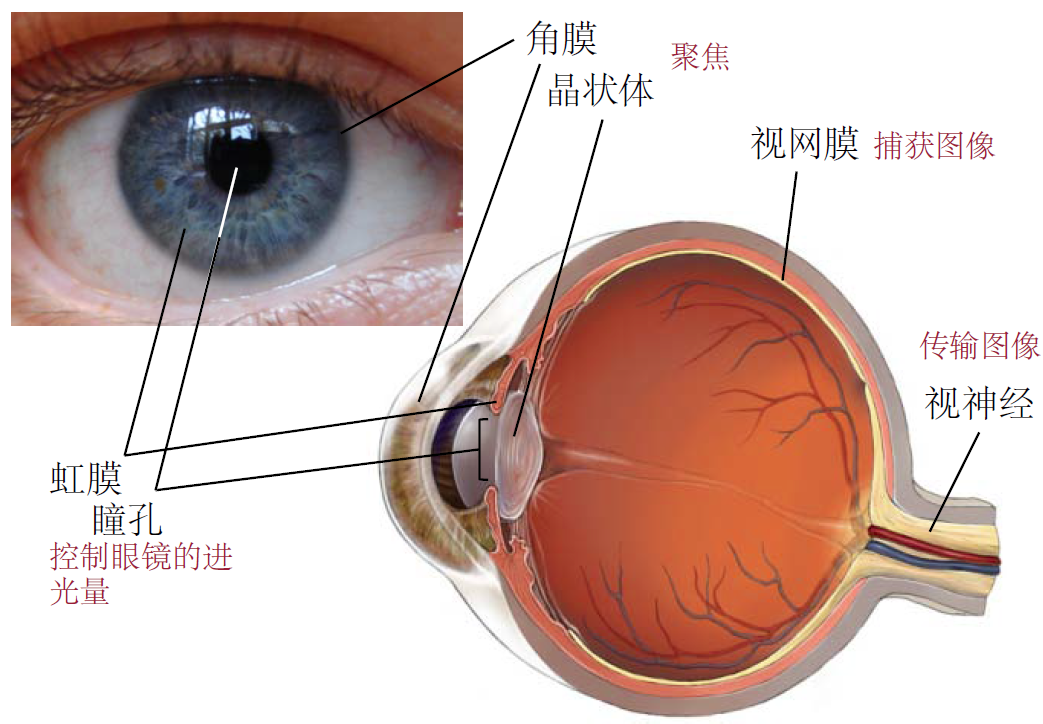
类比来说，相机就是计算机的“眼睛”：

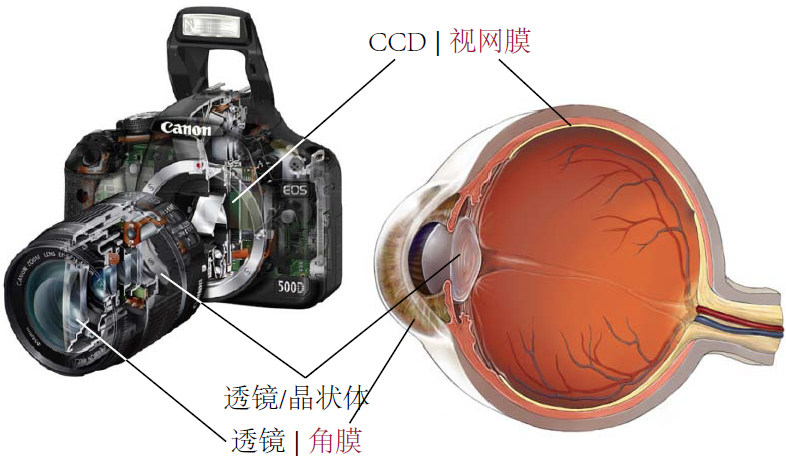
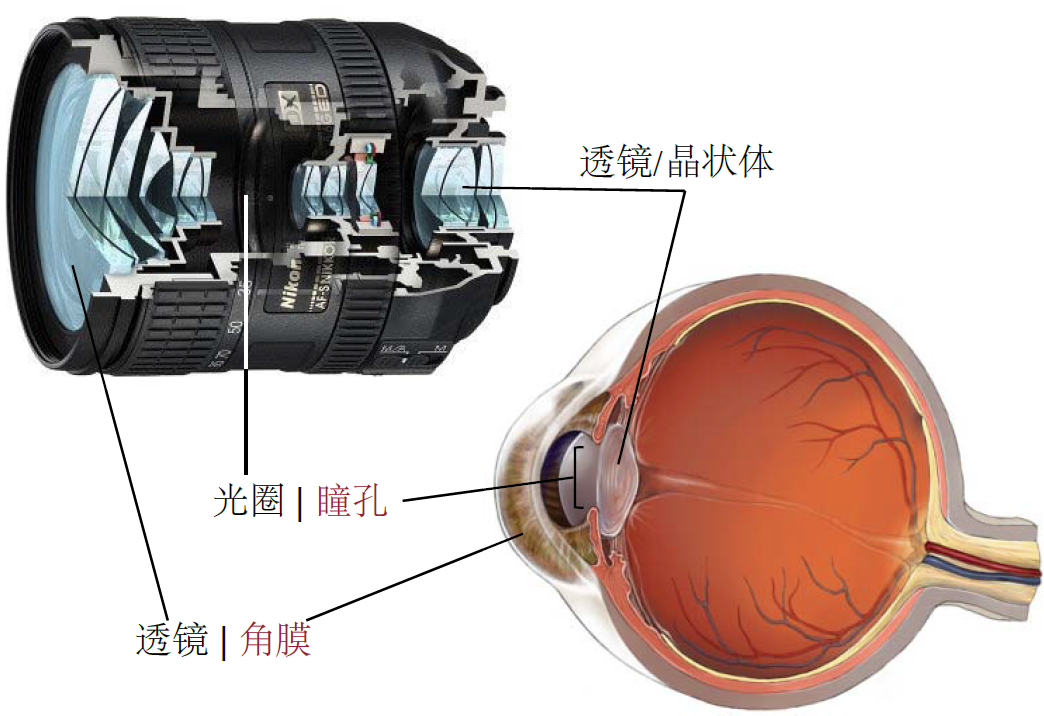
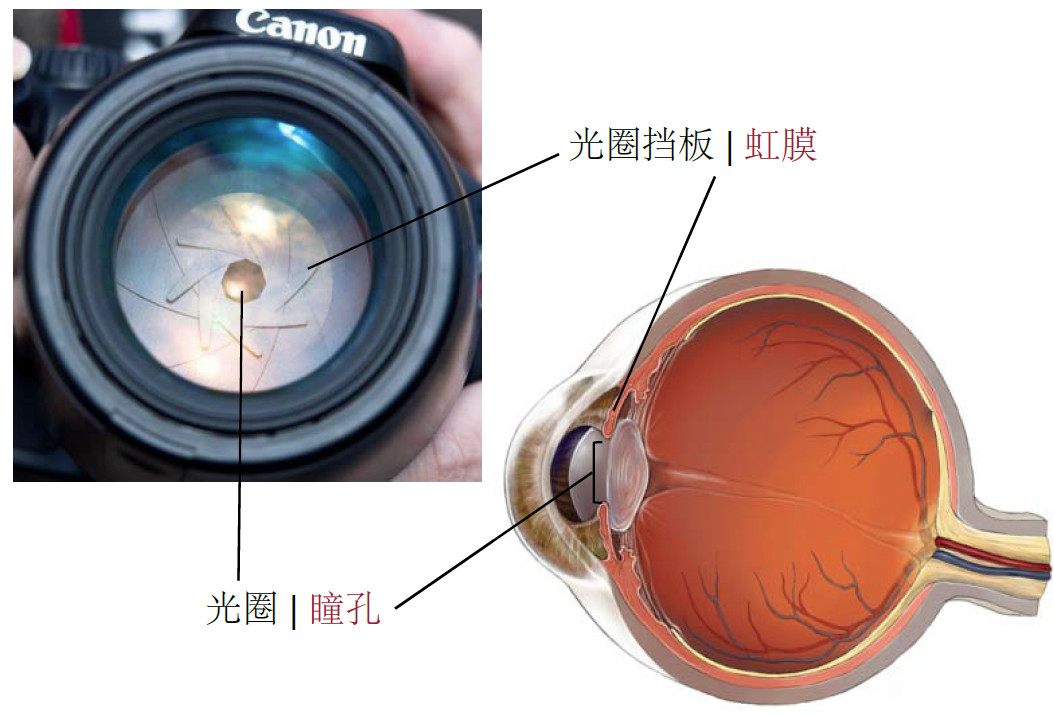
1.2 成像

本质上来说，图像是真实世界场景中在二维平面（成像平面）的投影，它记录了两类信息：

• 几何信息：位置、点、线等；
• 光度信息：强度、色彩。

2 相机成像模型

• 小孔成像模型（Pinhole camera model）
• 正交投影（Orthographic projection）
• 缩放正交投影（Scaled orthographic projection）
• 透视投影（Perspective projection）

2.1 小孔成像模型（Pinhole camera model）

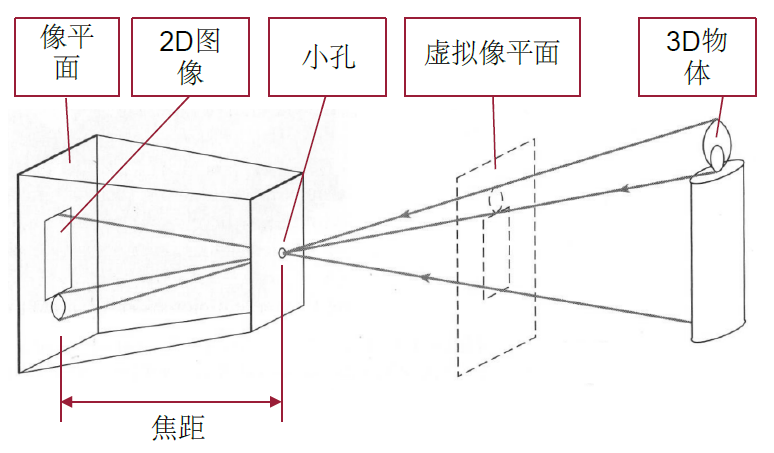
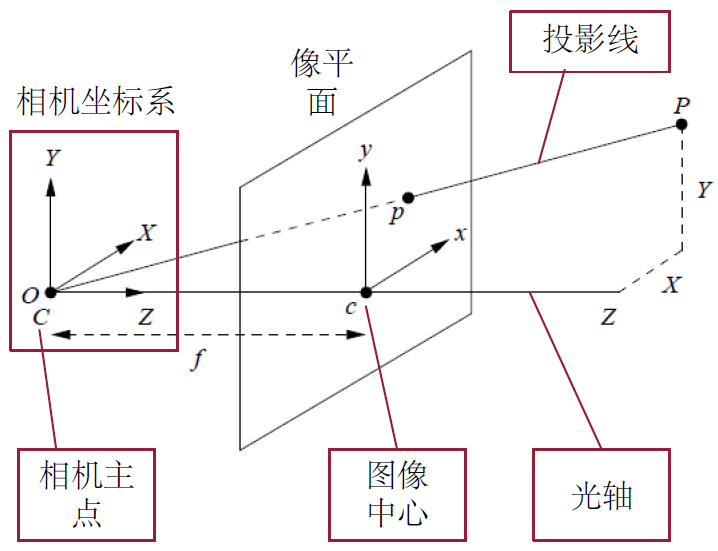
数学表示，具体也可参考博客：

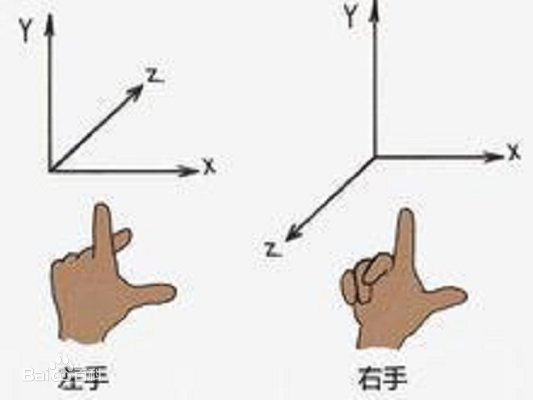
一般来说，我们使用右手坐标系：

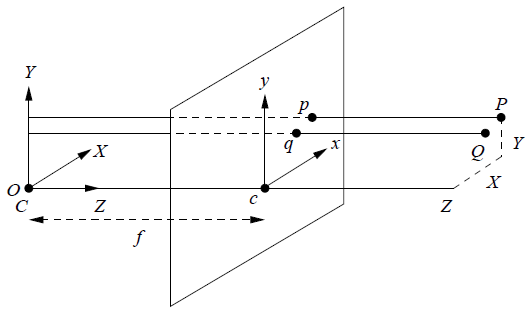
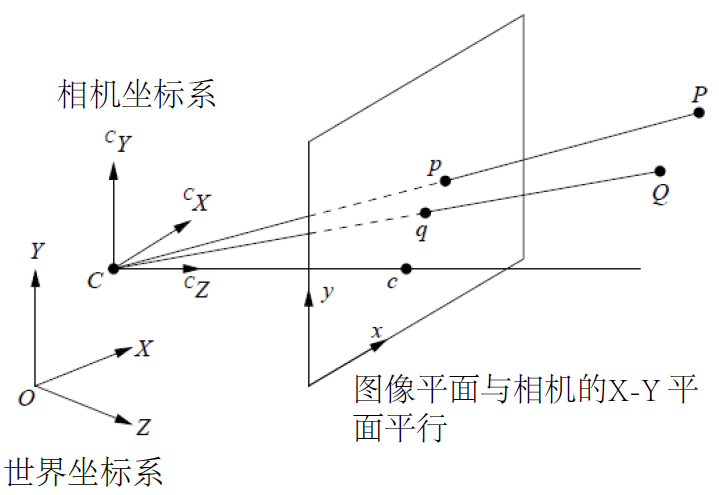
小孔成像模型实际上是透视投影（perspective projection）的一种最简单的形式。假设我们要将真实世界中的三维点$(X,Y,Z{)}^T$投影为二维图像上的点$p=(x,y{)}^T$，则有：

$$\{\begin{array}{l}\frac{X}{Z}=\frac{x}{f}\\ \frac{Y}{Z}=\frac{y}{f}\end{array}\Rightarrow \{\begin{array}{l}x=f\frac{X}{Z}\\ y=f\frac{Y}{Z}\end{array}\text{\hspace{1em}(1)}$$

2.2 正交投影（Orthographic projection）

• 3D场景距离相机无限远；
• 所有投影线均平行于光轴。

则有$x=X,y=Y$。

2.3 缩放正交投影（Scaled orthographic projection）

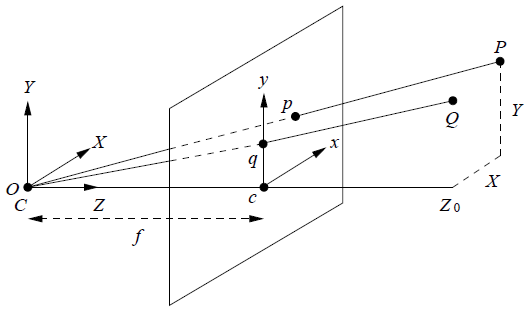
• 场景深度<<到相机的距离；
• 场景中所有点的Z值均相同，如$Z_0$。

这种情况相当于对垂直于相机Z轴方向上的一个平面场景进行成像，则对于场景中所有的点有：$x=sX,y=sY,s=\frac{f}{Z_0}$。

2.4 透视投影（Perspective projection）

3 相机参数

对于小孔成像模型中，有：

$$\{\begin{array}{l}x=f\frac{X}{Z}\\ y=f\frac{Y}{Z}\end{array}\text{\hspace{1em}(2)}$$

3.1 相机内参

上述为理想状态下的公式，下面来分析几种特殊情况。

3.1.1 像素不是正方形

当相机传感器（CCD）上的像素不是正方形时有：

$$\{\begin{array}{l}x=kf\frac{X}{Z}\\ y=lf\frac{Y}{Z}\end{array}\text{\hspace{1em}(3)}$$

• x，y：坐标（pixel）；
• k，l：缩放因子（pixel/mm）
• f：焦距（mm）

令上式中：$f_x=kf,f_y=lf$，则有：

$$\{\begin{array}{l}x=f_x\frac{X}{Z}\\ y=f_y\frac{Y}{Z}\end{array}\text{\hspace{1em}(4)}$$

3.1.2 相机主点（principal point）不在原点

即光轴与CCD中心有偏移。假设主点在图像上的坐标（像素）为$c_x,c_y$，则有：

$$\{\begin{array}{l}x=f_x\frac{X}{Z}+c_x\\ y=f_y\frac{Y}{Z}+c_y\end{array}\text{\hspace{1em}(5)}$$

那么沿着相机的Z轴，有$X=Y=0$，$x=c_x,y=c_y$。

3.1.3 x轴与y轴不垂直

理想情况下，x轴与y轴是相互垂直的，但一般情况下，x轴和y轴的夹角并不是90度。假设x轴和y轴之间的夹角为$\theta$，则有：

$$\{\begin{array}{l}x=f_x\frac{X}{Z}-f_{x}cot\theta \frac{Y}{Z}+c_x\\ y=\frac{f_y}{sin\theta }\frac{Y}{Z}+c_y\end{array}\text{\hspace{1em}(6)}$$

3.1.4 内参矩阵

组合所有参数，可以得到相机的内参矩阵$K$：

$$K=\left[\begin{array}{ccc}{f}_x& -f_{x}cot\theta & c_x\\ 0& \frac{f_y}{sin\theta }& c_y\\ 0& 0& 1\end{array}\right]＝\left[\begin{array}{ccc}{f}_x& s& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\text{\hspace{1em}(7)}$$

3.2 相机外参

相机外参反映了相机在世界坐标空间中的位姿，可通过一个刚性变换来表示，通常包含平移$T$和旋转$R$。

平移矩阵：

$$T=\left[\begin{array}{c}{T}_X\\ T_Y\\ T_Z\end{array}\right]\text{\hspace{1em}(8)}$$

旋转矩阵：

$$R=\left[\begin{array}{ccc}{r}_{1}1& r_{1}2& r_{1}3\\ r_{2}1& r_{2}2& r_{2}3\\ r_{3}1& r_{3}2& r_{3}3\end{array}\right]\text{\hspace{1em}(9)}$$

旋转矩阵是正交的，所以有：$R^{T}R=I$。

4 畸变

畸变是光学透镜固有的透视失真特性，目前所有的镜头都存在畸变，只是程度不同。畸变又分为径向畸变和切向畸变，这里只以径向畸变为例。常见的径向畸变有桶形畸变、枕形畸变等：

径向畸变可以被建模为：

具体的畸变校正过程可以参考博客。

5 相机标定

相机标定的目的就是获取前文提到的相机内参、外参和畸变系数。通常，标定方法分为两步：（1）从不同角度捕获棋盘格图像；（2）检测角点并计算相机参数。

可使用OpenCV或其他相机标定程序来完成参数计算。

参考

[1] 一个pdf，下载地址找不到了=_=

最后

以上就是着急小海豚为你收集整理的相机标定（三）-相机成像模型1 人眼&相机结构2 相机成像模型3 相机参数4 畸变5 相机标定的全部内容，希望文章能够帮你解决相机标定（三）-相机成像模型1 人眼&相机结构2 相机成像模型3 相机参数4 畸变5 相机标定所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。