说明：阅读本文章的前提是对堆排序过程有大致了解，此处重点讲解算法的复杂度

堆排序的过程

每次交换堆顶元素和堆底元素之后，待排序元素个数就少一个

初始状态

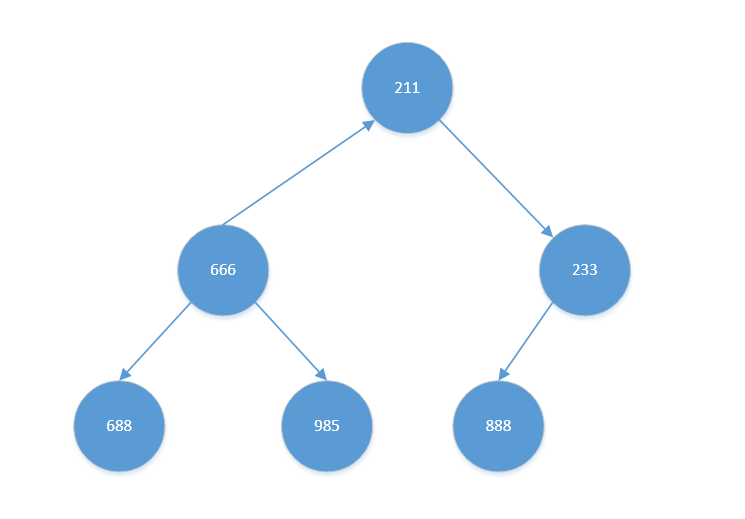
建立初始堆（大根堆）

依次从后往前逐渐调整，只考虑非叶子节点（分支节点），第一个调整的元素为“最后一个非叶子节点”，即【233】

1. 考虑【233】

其左孩子为【888】，无右孩子。【888】比【233】大，交换【233】与【888】。结果如下：

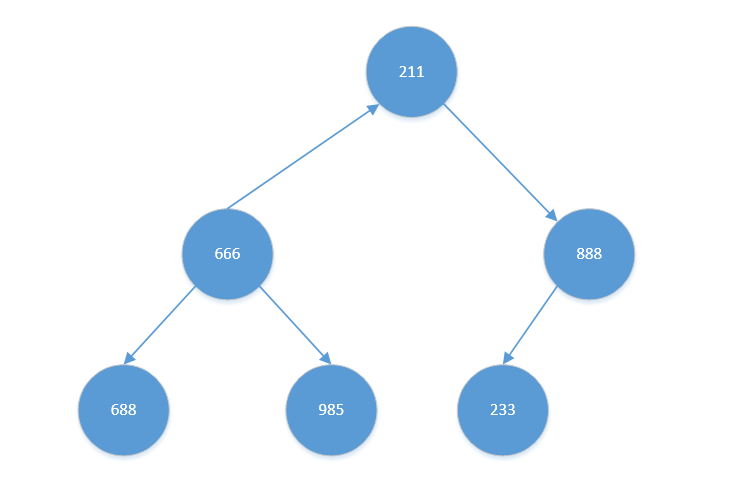
交换后，【233】无孩子节点，无需继续考虑【233】

2. 考虑【666】

其左右孩子中，【985】比【688】大。且【985】比【666】也大，交换【666】与【985】。结果如下：

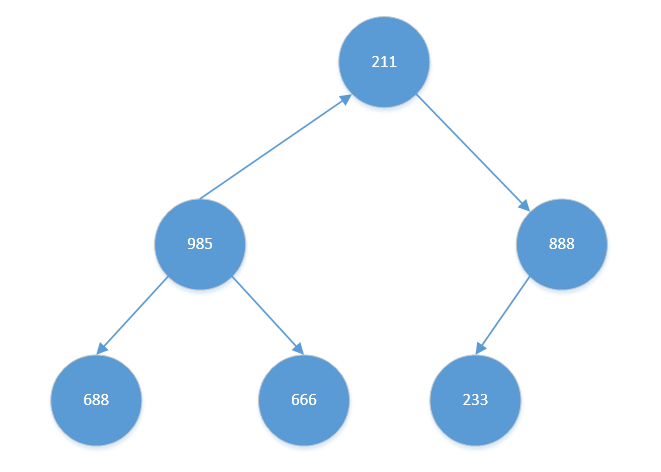
交换后，【666】无孩子节点，无需继续考虑【666】

3. 考虑【211】

其左右孩子中，【985】比【888】大。且【985】比【211】也大，交换【211】与【985】。结果如下：

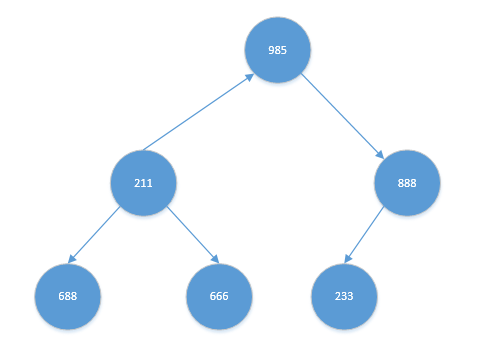
交换后，【211】有孩子节点。其左右孩子中，【688】比【666】大。且【688】比【211】也大，交换【211】与【688】。结果如下：

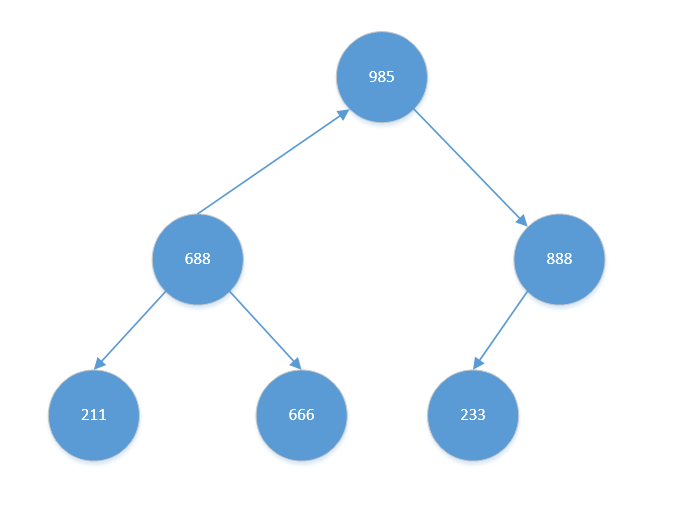
至此，已建立大根堆

交换堆顶元素与堆底元素，并重新调整大根堆

• 将堆顶元素【985】与堆底元素【233】交换。结果如下：
  

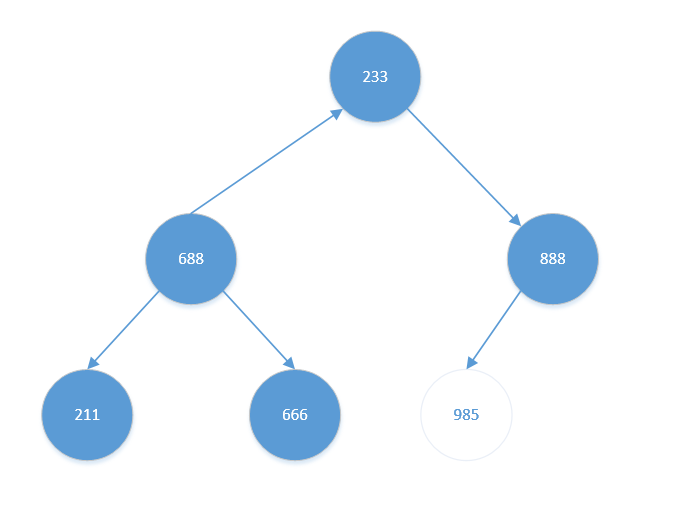
此时待排序元素（前5个）已不是大根堆，需要重新调整为大根堆

考虑堆顶元素【233】
其右孩子【888】比左孩子【688】更大。且【888】比【233】也大。交换【233】与【888】。结果如下：

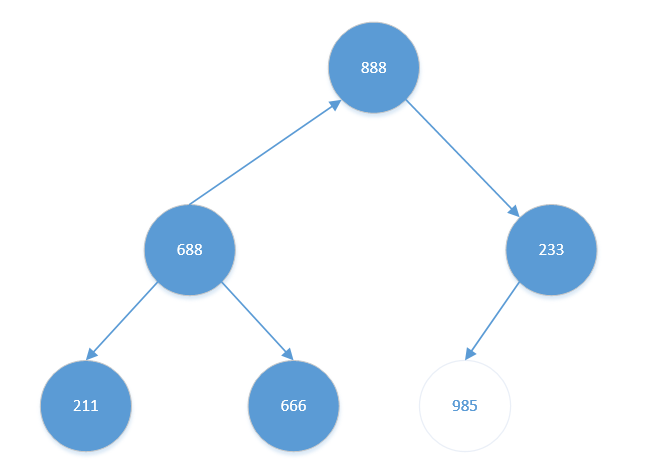
交换后，【233】无孩子节点（985为排好序的元素），无需继续考虑【233】

• 将堆顶元素【888】与堆底元素【666】交换。结果如下：
  

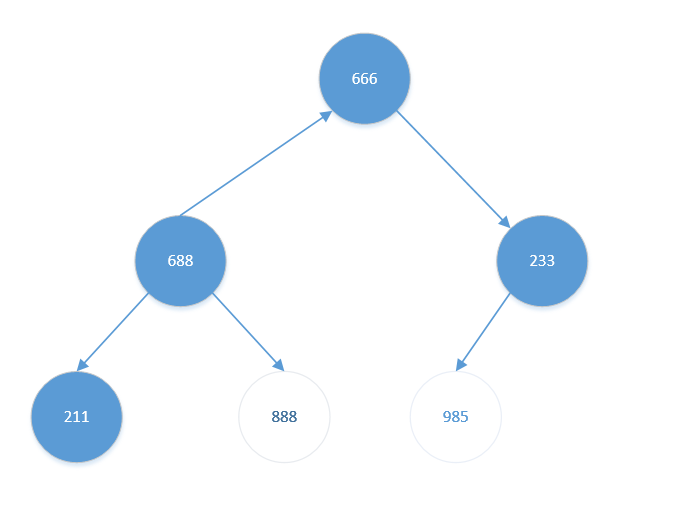
此时待排序元素（前4个）已不是大根堆，需要重新调整为大根堆

考虑堆顶元素【666】
其左孩子【688】比左孩子【233】更大。且【688】比【666】也大。交换【666】与【688】。结果如下：

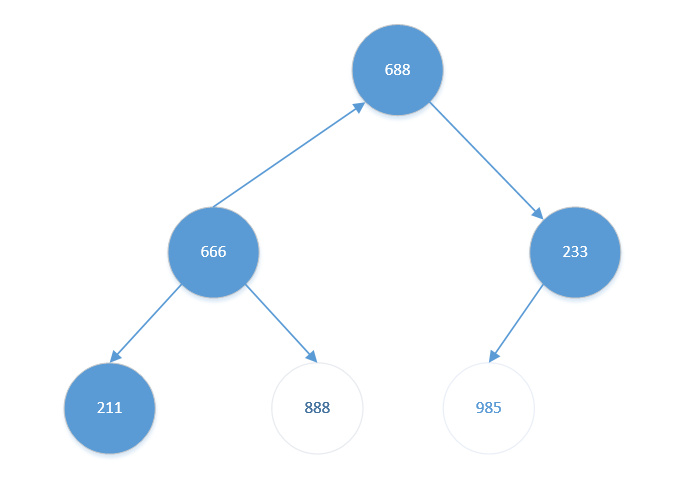
交换后，【666】有左孩子节点【211】（888为排好序的元素），但【211】比【666】小，不再进行调整

• 将堆顶元素【688】与堆底元素【211】交换。结果如下：
  

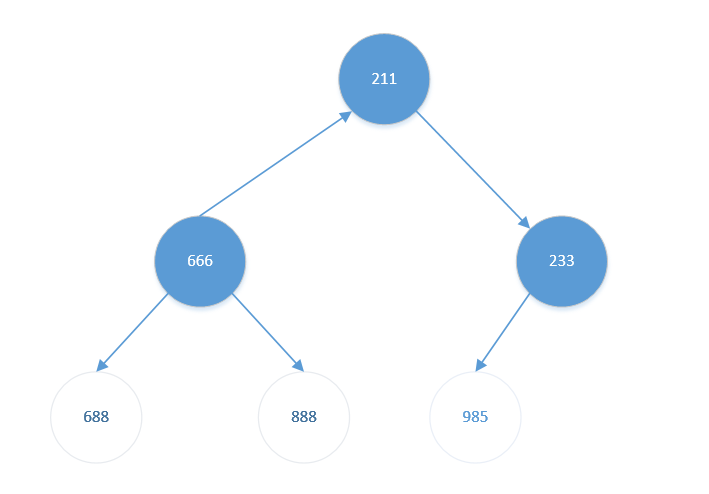
此时待排序元素（前3个）已不是大根堆，需要重新调整为大根堆

考虑堆顶元素【211】
其左孩子【666】比左孩子【233】更大。且【666】比【211】也大。交换【211】与【666】。结果如下：

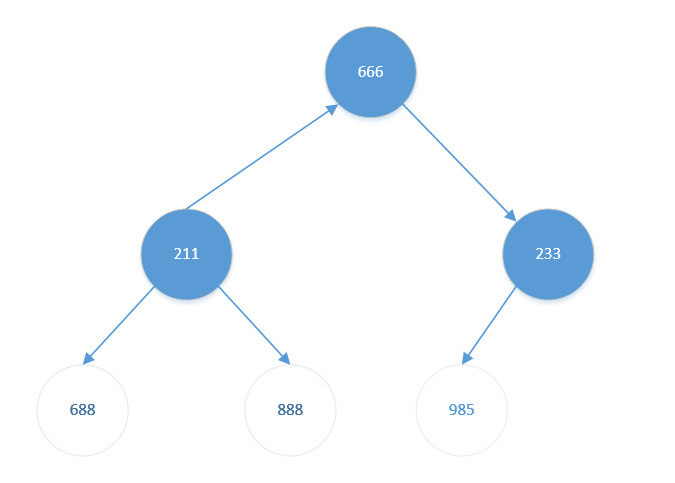
交换后，【211】无孩子节点（688、888为排好序的元素），无需继续考虑【211】

• 将堆顶元素【666】与堆底元素【233】交换。结果如下：
  

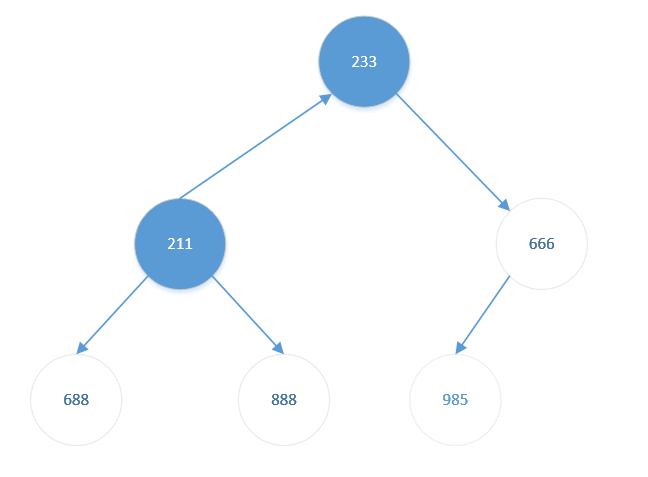
此时待排序元素（前2个）仍是大根堆，无需调整

• 将堆顶元素【233】与堆底元素【211】交换。结果如下：
  

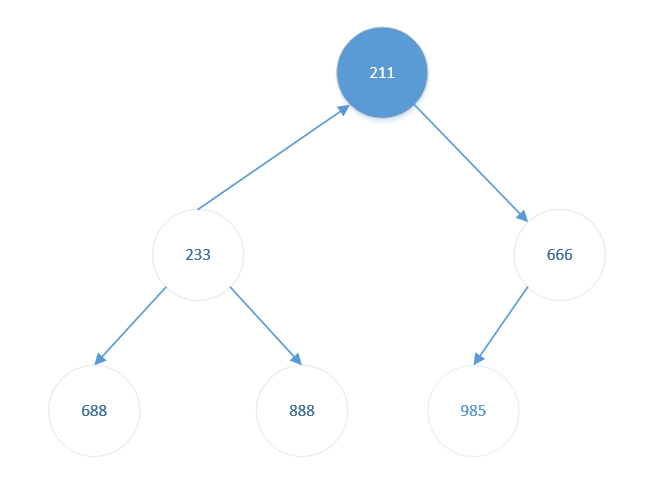
此时待排序元素（前1个）仍是大根堆，无需调整。

排序完成（升序），211<233<666<688<888<985

时间复杂度

建堆的时间复杂度

在调整堆时，每交换一次节点，最多比较关键字2次

• 比较1次：目标节点只有左孩子，无右孩子，将目标节点与其左孩子比较1下
• 比较2次：目标节点左右孩子均有，首先左右孩子先比较1下，然后大者再与目标节点比较1下

若目标节点在$x$层，树高为$h$，则调整时，目标节点最多交换$(h-x)$次，每次最多比较2次关键字，故$x$层节点的关键字对比次数不超过$2\times (h-x)$次

假设一颗完全二叉树，树高为h，最后一层节点无需进行调整
第1层共有1个节点，关键字对比次数最多为$1\times 2\times (h-1)$次
第2层共有2个节点，关键字对比次数最多为$2\times 2\times (h-2)$次
第h-1层共有2^h-2个节点，关键字对比次数最多$2^{h-2}\times 2\times 1$次
将整颗树调整为大根堆，关键字对比次数最多$1\times 2\times (h-1)+2\times 2\times (h-2)+...+2^{h-2}\times 2\times 1$次

处理上式为：${\sum }_{i=1}^{h-1}{2}^{i-1}\times 2\times (h-i)={\sum }_{i=1}^{h-1}{2}^i\times (h-i)$
由于n个节点的完全二叉树的高$h={\log }_{2}n+1$（向下取整）
$令j=h-i，则i=h-j。$原式$={\sum }_{j=h-1}^1{2}^{h-j}\times j={\sum }_{j={\log }_{2}n}^1{2}^{{\log }_{2}n+1-j}\times j={\sum }_{j={\log }_{2}n}^{1}n\times 2\times 2^{-j}\times j=2n\times {\sum }_{j={\log }_{2}n}^1{2}^{-j}\times j$

考虑$S_n={\sum }_{j=h}^1{2}^{-j}\times j={\sum }_{j=1}^h{2}^{-j}\times j=1\times \frac{1}{2}+2\times \frac{1}{4}+3\times \frac{1}{8}+...+h\times \frac{1}{2^h}$ ①
将$①\times \frac{1}{2}$ 得 $\frac{1}{2}{S}_n=1\times \frac{1}{4}+2\times \frac{1}{8}+...+(h-1)\times \frac{1}{2^h}+h\times \frac{1}{2^{h+1}}$ ②
使用错误相减法②-①得： $\frac{1}{2}{S}_n=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{2^h}-h\times \frac{1}{2^{h+1}}=\frac{\frac{1}{2}(1-\frac{1}{2^n})}{1-\frac{1}{2}}-h\times \frac{1}{2^{h+1}}=1-\frac{1}{2^n}-\frac{h}{2^{h+1}}$ ③
将$③\times 2$得：$S_n=2-\frac{1}{2^{h-1}}-\frac{h}{2^h}$④
很明显④式小于2即$S_n<2，所以2n\times {\sum }_{j={\log }_{2}n}^1{2}^{-j}\times j<4n$

建堆的时间复杂度为O(n)

交换堆顶底元素后重建堆的时间复杂度

每次将堆顶元素与堆底元素进行交换后，需要将剩余待排序元素重新建堆。此时处理的是堆顶元素，即根节点。根节点位于第一层，关键字最多比较次数为$2\times (h-1)$次。
上述过程共需进行n-1次（n为节点个数），故重建堆的总的关键字最多比较次数为$2\times (h-1)\times (n-1)=2{\log }_{2}n(n-1)$

重建堆的时间复杂度为O(nlogn)

堆排序的时间复杂度为O(nlogn)+O(n)=O(nlogn)

空间复杂度

整个排序过程，包括初建堆、交换顶底元素、重建堆，未用到其他多余的空间，主要进行比较与交换工作，所以空间复杂度是O(1)

最后

以上就是羞涩乌龟为你收集整理的【数据结构】堆排序的算法复杂度分析堆排序的过程时间复杂度空间复杂度的全部内容，希望文章能够帮你解决【数据结构】堆排序的算法复杂度分析堆排序的过程时间复杂度空间复杂度所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。