优化堆排序

基础排序出现的问题：

在上一个基本的堆排序中我们会发现这样一个问题：左节点和右节点虽然满足了小于父节点，但是左节点和右节点的大小是没有比较的，所以反映回数组，就不能满足完全的从小到大或者从大到小的排序，会出现两个相邻的数大小顺序出错的情况，同时不同父节点下的数没有比较，也会出现出错的情况。具体反应如图：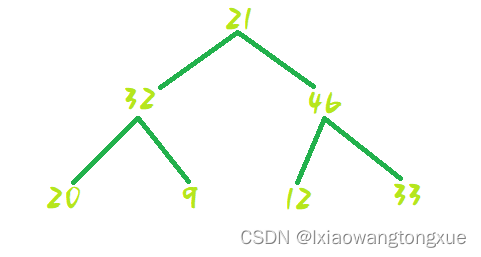

排序完以后：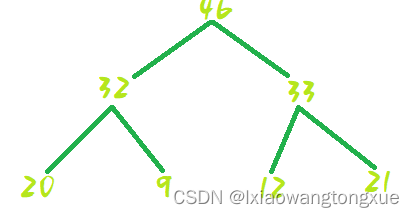 

体现在数组上就是：

21 32 46 20 9 12 33 排序后为 46 32 33 20 9 12 21 我们可以看到这个并不是严格的排序

解决思路：

但是我们可以发现基础排序有一点是确定的，就是每一次排序后第一个数一定是这组数中最大的。那我们就把最大的数依次拿出来完成一个排序。也就是每一次都把第一个数取出，然后把最后一位数放到第一位，接着shiftDown获取下一个最大的数，拿出来的数按顺序就完成了完全的排序。演示如图：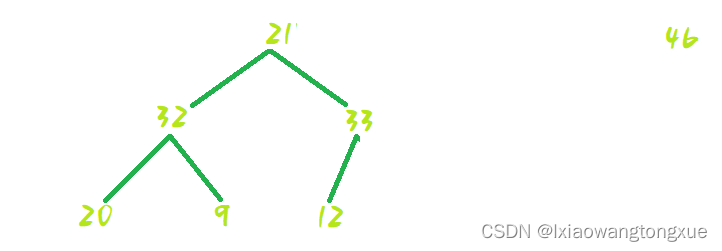

shiftDown:

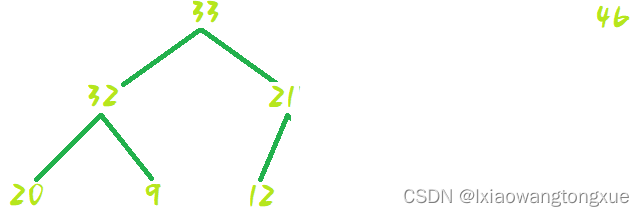
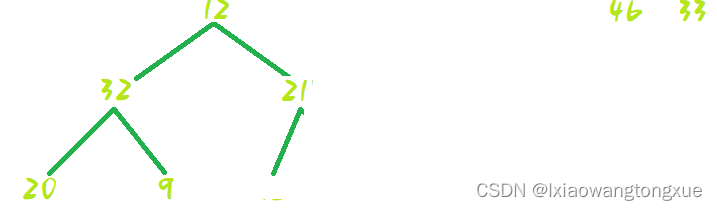然后shiftDown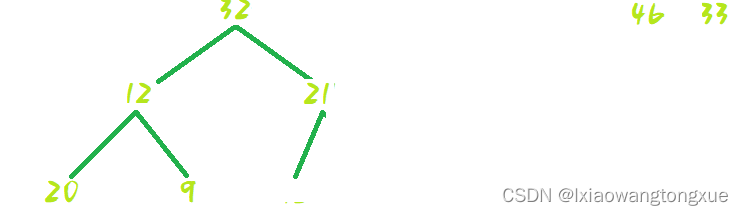 

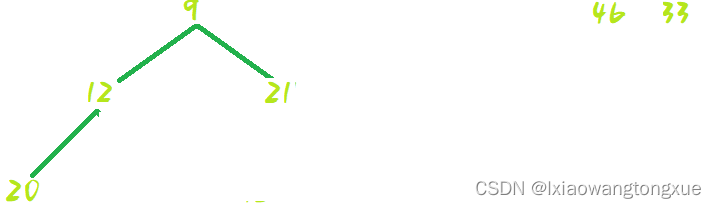 然后shiftDown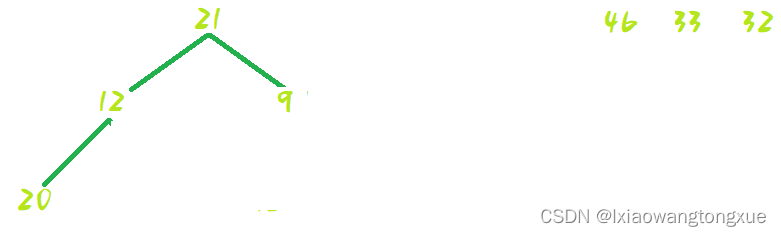  

shiftDown

将12取出和9取出，完成排序

在有了一个大概思路以后，为了减少空间的浪费，我们可以就在原数组身上操作，每次把第一个数与操作数组的最后一个数交换，已经排好顺序的数不再参与shiftDown:

具体反映到堆上是这样的，我们依旧用之前的例子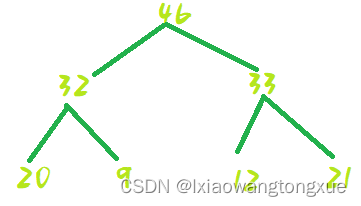 

交换位置：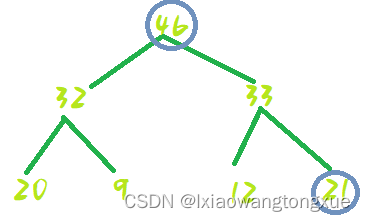 

21---12处shiftDown：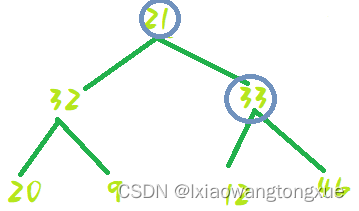 

交换位置： ​​​​​​​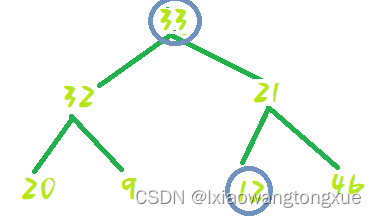

12---9处shiftDown: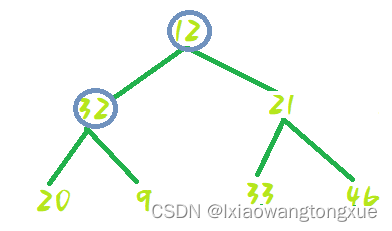  

交换位置：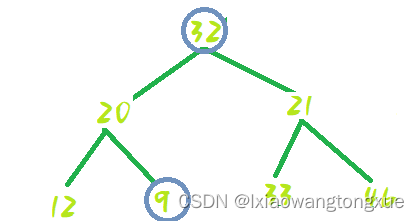 

9---12处shiftDown：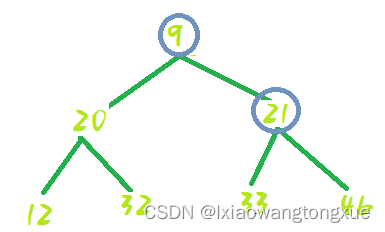 

交换位置：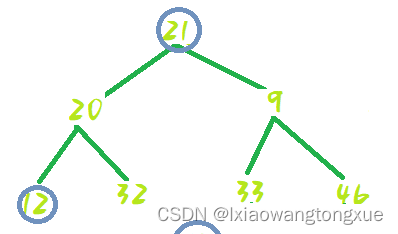 

12--9处shiftDown：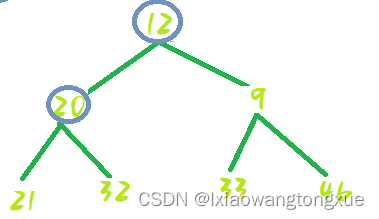   

交换位置：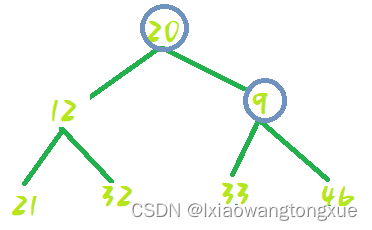 

9---12处shiftDown：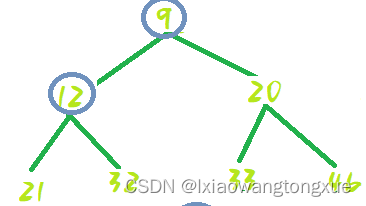 

交换位置：​​​​​​​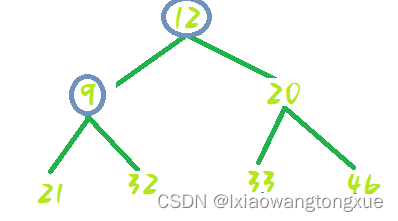 

完成排序：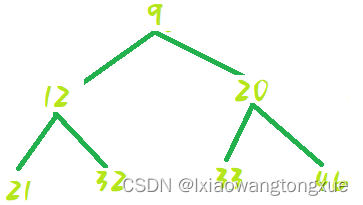  

代码展示：

package CSDN;

public class HeapSort<T extends Comparable>{
    public void sort(Comparable[] arr){
        int n = arr.length;
        //此时索引从0开始，最后一位的索引为n-1
        for (int i = (n-1-1)/2; i >= 0; i--) {//初步排序，另一篇文章有介绍
            shiftDown(arr,i,n);
        }

        for (int i = n-1; i >0 ; i--) {//每次都选出最大的排在之前的后一位，最后实现严格的从小到大的排序
            swap(arr,i, 0 );
            shiftDown(arr,0,i);
        }
    }

    public void shiftDown(Comparable[] arr, int k, int n){
        while (2*k+1 < n ){//k有左节点
            int j = 2*k+1;
            //下面的操作是选出右节点和左节点中最大的
            if (j+1 < n && arr[j+1].compareTo(arr[j]) > 0){//右节点存在，右节点大于左节点
                j += 1;
            }
            if (arr[k].compareTo(arr[j])>0) break;//如果k父节点比其子节点最大的都大，说明此时k的位置是正确的
            swap(arr, j , k);//否则，交换k与子元素最大元素的位置
            k = j;
        }
    }

    public void swap(Comparable[] arr, int i, int j){
        Comparable c = arr[i];
        arr[i] = arr[j];
        arr[j] = c;
    }

    public static void main(String[] args) {
        Integer[] arr = {1,33,42,54,23,44,75,52};
        HeapSort<Integer> heapSort = new HeapSort<>();
        heapSort.sort(arr);
        for (Integer i:arr) {
            System.out.print(i+" ");
        }
    }
}

 需要注意的问题：

1.

int n = arr.length;
    //此时索引从0开始，最后一位的索引为n-1
    for (int i = (n-1-1)/2; i >= 0; i--) {//初步排序，另一篇文章有介绍
        shiftDown(arr,i,n);
    }

 我们可以看到这里与之前的表示方式不太一样，包括后面左节点为2*k+1右节点为2*k+2，这是因为索引与之前不一样了，之前我们是把数据装到一个新的数组里，0位置没有装入，从1开始装的，而现在是从0开始装，所以表示方式相应出现了一些改变

2.

for (int i = n-1; i >0 ; i--) {//每次都选出最大的排在之前的后一位，最后实现严格的从小到大的排序
    swap(arr,i, 0 );
    shiftDown(arr,0,i);
    }

 这里判断条件为i>0是因为i等于0时不用再参与判断了，此时在这个位置上的一定为最小的数

最后

以上就是温暖犀牛为你收集整理的优化堆排序的全部内容，希望文章能够帮你解决优化堆排序所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。