目录

一. 向上调整算法

二.向下调整算法

三.堆排序

#向上调整建堆

#向下调整建堆

#堆排序时间复杂度

#堆排序的应用

TOP —K问题

数据结构中的堆的一些功能实现中涉及到了向上调整算法与向下调整算法，用这两个算法可以实现堆排序。原理是这两个算法可以把小堆中的最小的数或者大堆中最大的数排到堆顶，将堆顶的数隔离开再进行调整，以此类推每次都可以将最大的数或者最小的数单独拎出来，重复以上操作即可排序。

关于堆的文章在上一篇

https://blog.csdn.net/qq_62236390/article/details/125772030

以小堆为例，理一下两个算法。

一. 向上调整算法

当我们想要往堆中插入一个数据时，这个数据可以比父节点大，也可以比父节点小，那么我们如何保证插入数据后这个结构仍是堆呢？可以拿着这个数据(孩子)一路向上探索，因为是小堆，所以如果其父节点比孩子大，那么就要交换，交换之后将目前父节点位置赋给孩子，更新父节点位置，继续向上探索。如果子节点比父节点大，那么则停止这个过程(因为原本的数组就是一个堆，是满足堆的性质的，如果这个数据比其父节点大，那么一定比它的祖先大，所以不用再进行调整),这就是向上调整算法。

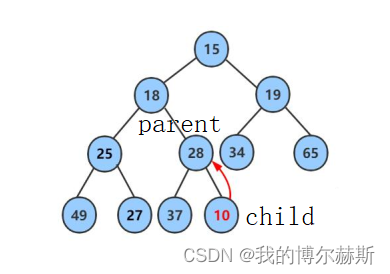
                                            图一

以这课二叉树为例解释一下向上调整算法， 此时的child是最后一个节点10，父节点是28(根据子节点和父节点的关系计算，可以看上一篇文章)，28比10大，因为是小堆所以要交换二者的值，并将原来28的位置(即parent)赋给原来10的位置(即child)。然后更新parent的位置到18. 如图二示

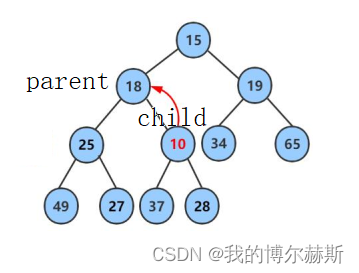
                                      图二

当这个过程循环下去，结束循环的条件无非是两种，要么child没有了父节点，即走到了终点。要么在半路上child节点的值小于其父节点的值，所以我们可以写出代码如下

#include <stdio.h>

//交换函数
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
void AdjustUp(int* a, size_t size)
{
	size_t child = size - 1;
	size_t parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[parent] > a[child])
		{
			Swap(&a[parent], &a[child]); //交换child 和 parent
			child = parent;              //更新child
			parent = (child - 1) / 2;    //更新parent
		}
		else
		{
			break;
		}
	}
}

二.向下调整算法

向上调整算法是由插入数据引出的，而向下调整则是由删除数据引出的。我们这里说的删除并不是在任意位置删除，而是删除堆顶的元素，删除后我们同样遇到那个问题：删除数据后如何保证其还是堆。如果我们直接删除堆顶数据，这个时候怎么设计算法来调整呢？如果把两个子节点中较小元素直接置为堆顶元素的话，会破环掉这个堆的结构，原来的父子关系会被打乱。

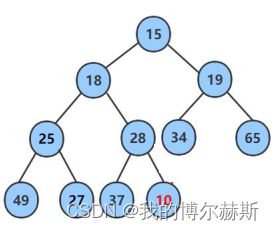
                             图三 

如图三示，如果这时候删除掉15，然后把18，19中的较小值18顶上去成为堆顶元素,那么原本示18的子节点的25和28就不再会是18的子节点了，这个堆的结构发生了改变不便于进行操作。那么可不可以有没有一种不影响原来堆结构并且能成功删除堆顶元素的操作呢？答案当然是有的。

操作步骤是：先交换堆顶元素与堆底元素，然后删除掉堆底元素，这样就把原来的堆顶元素删除掉了，同时并没有影响到堆顶元素意以外的各元素的结构

在进行上述操作后，原来的堆底元素到了堆顶，使得这颗树不满足堆的性质，那么这个时候就需要向下调整，让这个“冒牌货”沉下去。

和向上调整的原理类似，向下调整即取出孩子节点中较小的(以小堆为例)那个与父节点比较，如果父节点比它大，那么交换二者的值，然后更新位置。直到走到没有孩子或者父节点比子节点小的位置结束，要注意的是父节点可能没有右孩子，所以在选择较小孩子的时候要先判断右孩子是否存在，否则可能会越界。写出代码如下：

void AdjustDown(HP* php)
{
	size_t parent = 0;
	size_t child = parent * 2 + 1;
	while (child < php->size)
	{
		//访问右孩子, 得到二者中较小值
		if (child + 1 < php->size && php->x[child] > php->x[child + 1])//防止越界
		{
				++child;
		}
		//与父节点进行比较
		if (php->x[child] < php->x[parent])
		{
			Swap(php->x + child, php->x + parent);
			//更新parent和child
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

三.堆排序

问题：现在有一个数组arr = { 5，8， 9， 4， 3， 7}；如何用堆对其进行排升序。

答：可以先在数组的基础上建大堆，然后交换堆顶与堆底元素，再向下调整，再pop，依次类推，即可完成排序。

建堆的方式：

#向上调整建堆

从堆顶元素的左孩子开始往上调整，直到堆底元素结束。

void Heaparrup(HPDatatype* a, size_t size)
{
	int track = 1;
	while (track < size)
	{
		AdjustUp(a, track++);
	}
}

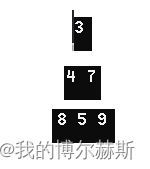
             图四

如图四示，运行上述代码后，数组中元素已经排成了小堆。

#向下调整建堆

同理向下调整建堆则是从第一个非叶子节点开始，到堆顶元素为止。

void Heaparrdown(HPDatatype* a, size_t size)
{
	for (int i = (size - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, size, i);
	}
}

 #建好堆之后进行排序，注意如果要排升序，那么要建大堆，排降序则建小堆。因为每次pop是把堆顶元素移动到最后，大堆堆顶元素是最大的，被挪到最后正合适。小堆同理。建堆并不是将元素排好序，而是将其中最大的选出来放在堆顶，随着一次次的选出最大的数并一次次的挪到最后，小的数就自然而然在前面，大的数自然而然在后面了。写出代码如下：

void Heaparrup(HPDatatype* a, size_t size)
{
	int track = 1;
	while (track < size)
	{
		AdjustUp(a, track++);
	}
	//
	size_t end = size;
	while (end > 0)
	{
		--end;
		Swap(&a[0], &a[size]);
		AdjustDown(a, size, 0);
	}
}

                            图五 

如图五示，由于我建的是小堆所以排成了降序，说明堆排序已经完成。

当想使用堆排序的时候，只需要在原有基础上建堆然后重复取堆顶元素就好。

#堆排序时间复杂度

对于向下调整建堆的时间复杂度

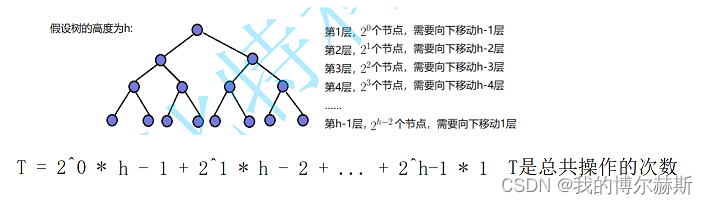
 以满二叉树为例，建好堆的时间复杂度是T，这里T的表达式是一个差比混合数列，可以利用错位相减法求出最后T = n - log(n + 1) ≈ n(因为n的变化率更大)。

所以排序算法的复杂度是n*logn，而空间复杂度是O(1）。

#堆排序的应用

TOP —K问题

在日常生活中我们总要在很多数据中选出最有代表性的k个(最大或最小)，比如说王者荣耀里的国榜，区榜等等。我们如果使用遍历的方式的话时间复杂度是O(n * n),当数据很多时，这个算法肯定效率极其低下。那么可以采用我们的堆排序。先创建一个容量为k的数组,然后插入k个数据，以这k个数据建堆，遍历后n-k个数据，与堆顶数据进行比较，如果比堆顶数据更满足堆的性质，则将其与堆顶数据交换，并向下调整，这样的算法时间复杂度是O(k + (n - k) * logk)，空间复杂度是O(k)，空间利用效率很高。

最后

以上就是震动导师为你收集整理的数据结构中的堆排序算法一. 向上调整算法二.向下调整算法三.堆排序的全部内容，希望文章能够帮你解决数据结构中的堆排序算法一. 向上调整算法二.向下调整算法三.堆排序所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。