堆排序时间复杂度实现代码时间复杂度初始化堆：O（n）

57 阅读 0 评论 38 点赞

我是靠谱客的博主雪白过客，最近开发中收集的这篇文章主要介绍堆排序时间复杂度实现代码时间复杂度初始化堆：O（n），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

注：本文转载于两篇博文，感谢博主

转载于：

https://blog.csdn.net/yuzhihui_no1/article/details/44258297

https://blog.csdn.net/qq_34228570/article/details/80024306

堆排序是由1991年的计算机先驱奖获得者、斯坦福大学计算机科学系教授罗伯特.弗洛伊德(Robert W．Floyd）和威廉姆斯(J．Williams）在1964年共同发明了的一种排序算法（ Heap Sort )；

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆，是完全二叉树。大根堆的要求是每个节点的值都不大于其父节点的值，即A[PARENT[i]] >= A[i]。在数组的非降序排序中，需要使用的就是大根堆，因为根据大根堆的要求可知，最大的值一定在堆顶。

算法分析
其实这种算法看起来挺复杂，但是如果真正理解了就会感觉非常简单的；

基本思想：把待排序的元素按照大小在二叉树位置上排列，排序好的元素要满足：父节点的元素要大于等于其子节点；这个过程叫做堆化过程，如果根节点存放的是最大的数，则叫做大根堆；如果是最小的数，自然就叫做小根堆了。根据这个特性（大根堆根最大，小根堆根最小），就可以把根节点拿出来，然后再堆化下，再把根节点拿出来，，，，循环到最后一个节点，就排序好了。

基本步骤：

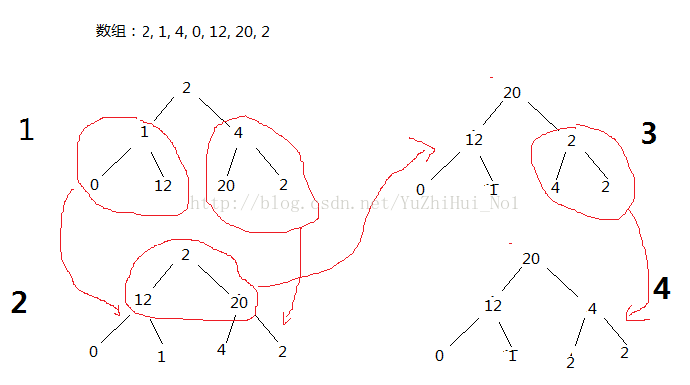
其实整个排序主要核心就是堆化过程，堆化过程一般是用父节点和他的孩子节点进行比较，取最大的孩子节点和其进行交换；但是要注意这应该是个逆序的，先排序好子树的顺序，然后再一步步往上，到排序根节点上。然后又相反（因为根节点也可能是很小的）的，从根节点往子树上排序。最后才能把所有元素排序好；具体的操作可以看代码，也可以看看下面的图示：

实现代码

理解代码：i节点的孩子节点为 2i +1和 2i+2 ；i节点的父节点为：(i-1)/2；最后一个非叶子节点：n/2 - 1；下面的代码是实现的大根堆，把元素从小到大依次排序；

#include<stdio.h>
 
 #define LEN 12
 //打印数组
 void print_array(int *array, int length)
 {
     int index = 0;
     printf("array:n");
     for(; index < length; index++){
         printf(" %d,", *(array+index));
     }
     printf("nn");
 }
 //堆化函数
 void _heapSort(int *array, int i, int length)
 {
     int child, tmp;
     //这个是改变了哪个节点，就从该节点开始对以该节点为根节点的子树进行排序
     for (; 2*i + 1 < length; i = child){//依次到它的子树的子树。。。。
         child = 2*i + 1;
         if ((child +1  < length) && (array[child+1] > array[child])) child++;//选个最大的孩子节点
         if (array[i] < array[child]){//最大子节点和父节点进行交互
             tmp = array[i];
             array[i] = array[child];
             array[child] = tmp;
         }else break;
     }   
 }
  
 void BuildMaxHeap(int *array, int length){//初始化堆
          int i;
          for (i = length/2 - 1; i >= 0; i--)  
              _heapSort(array, i, length);//从第一个非叶子节点开始排序，一直到根节点

 }

 void heapSort(int *array, int length)
 {
     int i, tmp;
 
     if (length <= 1) return;//如果元素小于1，则退出
     //这一步是先把元素都堆化好，后面的话 哪个节点修改过，就从哪个节点开始对以它为根节点的子树进行堆化

      //初始化堆  
      BuildMaxHeap(array, length);

     // 先抽取到根节点，然后再对元素进行堆化，然后又抽取根节点，再对元素进行堆化。。。。依次循环
     for (i = 0; i < length; i++ ){
         tmp = array[0];
         array[0] = array[length-i-1];
         array[length -i-1] = tmp;
         _heapSort(array, 0, length-1-i);//堆化子树
     }
 }


 
 int main(void)
 {
     int array[LEN] = {2, 1, 4, 0, 12, 520, 2, 9, 5, 3, 13, 14};
     print_array(array, LEN);
     heapSort(array, LEN);
     print_array(array, LEN);
     return 0;
 }

时间复杂度

初始化堆：O（n）

堆排序的时间复杂度，主要在初始化堆过程和每次选取最大数后重新建堆的过程；

初始化建堆过程时间：O(n)

推算过程：

首先要理解怎么计算这个堆化过程所消耗的时间，可以直接画图去理解；

假设高度为k，则从倒数第二层右边的节点开始，这一层的节点都要执行子节点比较然后交换（如果顺序是对的就不用交换）；倒数第三层呢，则会选择其子节点进行比较和交换，如果没交换就可以不用再执行下去了。如果交换了，那么又要选择一支子树进行比较和交换；

那么总的时间计算为：s = 2^( i - 1 ) * ( k - i )；其中 i 表示第几层，2^( i - 1) 表示该层上有多少个元素，( k - i) 表示子树上要比较的次数，如果在最差的条件下，就是比较次数后还要交换；因为这个是常数，所以提出来后可以忽略；

S = 2^(k-2) * 1 + 2^(k-3)*2.....+2*(k-2)+2^(0)*(k-1) ===> 因为叶子层不用交换，所以i从 k-1 开始到 1；

这个等式求解，我想高中已经会了：等式左右乘上2，然后和原来的等式相减，就变成了：

S = 2^(k - 1) + 2^(k - 2) + 2^(k - 3) ..... + 2 - (k-1) （注：说明时间复杂度与树的高度有关）

除最后一项外，就是一个等比数列了，直接用求和公式：S = { a1[ 1- (q^n) ] } / (1-q)；

S = 2^k -k -1；又因为k为完全二叉树的深度，所以 (2^k) <= n < (2^k -1 )，总之：可以认为k = logn （实际计算得到应该是 log(n+1) < k <= logn ）;

综上所述得到：S = n - logn -1，所以时间复杂度为：O(n)

排序重建堆：

　在取出堆顶点放到对应位置并把原堆的最后一个节点填充到堆顶点之后，需要对堆进行重建，只需要对堆的顶点调用_heapSort()函数。
　　每次重建意味着有一个节点出堆，所以需要将堆的容量减一。_heapSort()函数的时间复杂度k=log(n)，k为堆的层数。所以在每次重建时，随着堆的容量的减小，层数会下降，函数时间复杂度会变化。重建堆一共需要n-1次循环，每次循环的比较次数为log(i)，则相加为：log2+log3+…+log(n-1)+log(n)≈log(n!)。可以证明log(n!)和nlog(n)是同阶函数：
　　∵(n/2)n/2≤n!≤nn,∵(n/2)n/2≤n!≤nn,
　　∴n/4log(n)=n/2log(n1/2)≤n/2log(n/2)≤log(n!)≤nlog(n)∴n/4log⁡(n)=n/2log⁡(n1/2)≤n/2log⁡(n/2)≤log⁡(n!)≤nlog⁡(n)
　　所以时间复杂度为O(nlogn)
故堆排序（heapSort()）时间复杂度为：O(nlogn)