数字信号处理实验（一）——DTFT一、离散序列傅里叶变化——DTFT二、求LTI系统的频率响应H三、采样与重构

一、离散序列傅里叶变化——DTFT

1、DTFT公式

2、Matlab算法实现

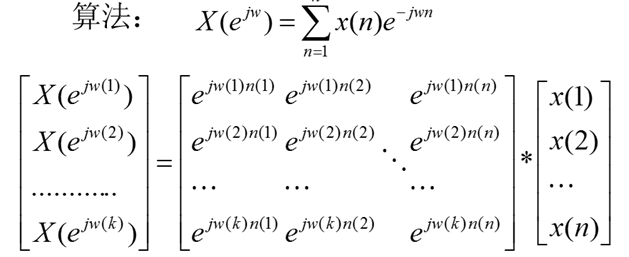
function[X]=dtft(x,n,w,flag)
%计算离散时间付里叶变换
%[X]=dtft(x,n,w)
%X=在w频率点上的DTFT数组
%x=n点有限长度序列
%n=样本位置向量
%w=频率点位置向量
X = x * (exp(-j).^(n' * w));

3、DTFT一些画图代码

function [] = signal_write(X,w,flag)
% X:数据
% w:频率向量
magX=abs(X);angX=angle(X);
realX=real(X);imagX=imag(X);
if(flag == 1)
figure();
magX=abs(X);angX=angle(X);
realX=real(X);imagX=imag(X);
subplot(2,2,1);plot(w/pi,magX);grid
xlabel('以pi为单位的频率');title('幅度部分');ylabel('幅度')
subplot(2,2,3);plot(w/pi,angX);grid
xlabel('以pi为单位的频率');title('相角部分');ylabel('弧度')
subplot(2,2,2);plot(w/pi,realX);grid
xlabel('以pi为单位的频率');title('实部');ylabel('实部')
subplot(2,2,4);plot(w/pi,imagX);grid
xlabel('以pi为单位的频率');title('虚部');ylabel('虚部')
end
if(flag == 2)
plot(w/pi,magX);grid
xlabel('以pi为单位的频率');title('幅度部分');ylabel('幅度')
end
if(flag == 3)
plot(w/pi,angX);grid
xlabel('以pi为单位的频率');title('相角部分');ylabel('弧度')
end
if(flag == 4)
plot(w/pi,realX);grid
xlabel('以pi为单位的频率');title('实部');ylabel('实部')
end
if(flag == 5)
plot(w/pi,imagX);grid
xlabel('以pi为单位的频率');title('虚部');ylabel('虚部')
end

 

 

二、求LTI系统的频率响应H

%example2.4
clear all;close all;
b=[1];
a=[1 -0.8];
m=0;length(b)-1;
l=0:length(a)-1;
%频率分点
K=500;
k=-2*K:1:2*K;
w=pi*k/K;
%构建分子和分母的傅里叶变换
num=b*exp(-j*m'*w); %分母
den=a*exp(-j*l'*w); %分子
h=num./den;
magH=abs(h);
angH=angle(h);
figure(1)
subplot(2,1,1);plot(w/pi,magH),grid,title('幅度部分')
subplot(2,1,2);plot(w/pi,angH),grid,title('相角部分')
n=0:100;
x=cos(0.05*pi*n);
y=filter(b,a,x);
figure(2)
subplot(2,1,1);plot(n,x),grid,title('输入信号')
subplot(2,1,2);plot(n,y),grid,title('输出信号')

 

三、采样与重构

Matlab代码

function [
] = caiyang(Fs,N,jt,flag)
%UNTITLED3 此处显示有关此函数的摘要
%
此处显示详细说明
%
Dt
模拟时间间隔：在特定精度下信号为模拟的
%
t
模拟时刻序列
%
n
离散时间索引
%
Ts
采样周期
%
Fs
采样频率
%
xa
在特定精度下，由离散信号逼近模拟信号
%
jt
是否需要重构
%
flag
5
第五题
%
6
第六题
Dt=0.00005;
% 模拟时间间隔：在特定精度下信号为模拟的
Ts=1/Fs;
% 采样周期
n=-N:1:N;
% 离散时间索引
nTs=n*Ts;
% 序列时刻索引
t=-N*Ts:Dt:N*Ts;
% 模拟时刻序列
%% 只是对应相应的作业、、
if flag == 5
xa=exp(-1000*abs(t));
% 在特定精度下，由离散信号逼近模拟信号
x1=exp(-1000*abs(nTs));
% Fs=5000 样本/s:x1为采样后的离散时间序列
end
if flag == 6
xa=sin(1000*pi*t);
% 在特定精度下，由离散信号逼近模拟信号
x1=sin(1000*pi*nTs);
% Fs=5000 样本/s:x1为采样后的离散时间序列
end
if flag == 7
xa = sin(20*pi*t + pi/4);
x1 = sin(20*pi*nTs + pi/4);
end
%%
K
= 500; % 对pi进行K等分:相当于对单位园2pi进行1000等分
dk = pi/K; % pi 的等分步进索引
w
= 0 : dk : pi; % 角度步进索引
X
= x1 * exp(-j* n'*w);% 对x1序列做离散傅立叶变换 
Xr = real(X);
w
= [-fliplr(w),w(2:end)]; % 定义w负半轴
Xr = [fliplr(Xr),Xr(2:end)]; % 由于实部偶对称，得到Xr的负半轴
%% 决定是否重构
if jt == 1
figure();
% 绘出xa
subplot(3,1,1)
plot(t*1000,xa);hold on
% 绘出x(jw)
stem(n*Ts*1000,x1,'r.'),hold off,title('时域波形')
% 绘出以pi归一化的数字频率对应的频域实部波形
subplot(3,1,2);plot(w/pi,Xr);title('频域波形')
subplot(3,1,3)
chonggou(x1,Fs,N);
end
if jt == 0
figure();
% 绘出xa
subplot(2,1,1);
plot(t*1000,xa);hold on
% 绘出x(jw)
stem(n*Ts*1000,x1,'r.'),hold off,title('时域波形')
% 绘出以pi归一化的数字频率对应的频域实部波形
subplot(2,1,2);plot(w/pi,Xr);title('频域波形')
end
if jt == 2
% 绘出以pi归一化的数字频率对应的频域实部波形
plot(w/pi,Xr);title('频域波形')
end
if jt == 3
figure();
subplot(2,1,1);
% 绘出xa
plot(t*1000,xa);hold on
% 绘出x(jw)
plot(n*Ts*1000,x1,'r.'),hold off,title('时域波形')
xa
= x1 * sinc(Fs*(ones(length(nTs),1) * t-nTs'*ones(1,length(t))));
% 内插重构

subplot(2,1,2);
plot(t*1000,xa, 'k' ),hold on
plot(n*Ts*1000,x1,'r.'),hold off ,title('重构波形' )
axis([-N/Fs*1000,N/Fs*1000,min(x1),max(x1)]);
end

 

重构代码：

function [
] = chonggou(x1,Fs,N)
%UNTITLED4 此处显示有关此函数的摘要
%
此处显示详细说明
%
x1 抽样序列
%
Fs 采样率
%
t
时间轴
%
Dt 离散间隔，模拟信号
Dt
= 0.00005;
% 模拟时间间隔：在特定精度下信号为模拟的
n
= -N:N;
nTs = n/Fs;
t
= -N/Fs:Dt:N/Fs;
% 模拟时刻序列
xa
= x1 * sinc(Fs*(ones(length(nTs),1) * t-nTs'*ones(1,length(t))));
% 内插重构

plot(t*1000,xa, 'k' ),hold on
stem(nTs*1000,x1, 'r.' ),hold off ,title('重构波形' )
axis([-N/Fs*1000,N/Fs*1000,min(x1),max(x1)]);
end