树状数组原理及经典应用问题

72 阅读 0 评论 48 点赞

我是靠谱客的博主甜美乐曲，最近开发中收集的这篇文章主要介绍树状数组原理及经典应用问题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

树状数组

对于数组相信大家并不陌生，那么为什么要在数组前面加上‘树状’二字呢？
数组是一种存储结构，树状数组是一种逻辑结构，它巧妙的应用了二进制的某些性质，使得数组的某些区间查询和修改变得非常的快，就像下面这个问题题目链接
如果用朴素方法解决这个问题，显然时间复杂度不过关，那么我们采用树状数组的思想来解决这个问题

lowbit

先看一个重要的函数

int lowbit(int x){
    return x & -x;
}

这个函数的作用是找到x所对应二进制数的最后一个1，一个数的负数在计算机里面使用补码存储，也就是把原数二进制取反再加1，也就是把二进制数1变0，0变1，再加上1，可以参考一下我这篇文章，那么对于数5，二进制为0101，那么-5的二进制数的补码应该是0101取反加1，即为1011，1011和0101做与操作，那么得到1，也就是说5的二进制从右往左第一个1应该在最后一位，可以证明lowbit操作总能找到二进制数最后一个1
lowbit的返回值是最后一个1和后面的0构成二进制数的十进制表示

使用

那么怎么使用lowbit来加速数组呢？需要使用数组建立一个逻辑上的森林结构，如下图
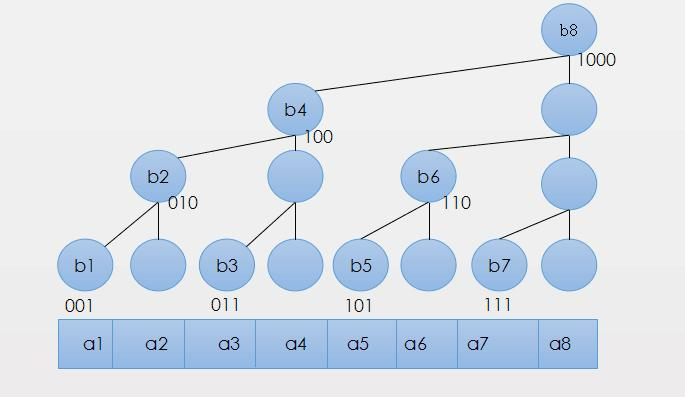
图上二进制数字就是下标对应的二进制数，可以发现，这个数组实际上构成了一棵树，所以称为树状数组

更改当前节点需要修改当前节点及其祖先节点，他的父亲节点下标是当前节点下标+=lowbit(x)，这样循环下去，可以修改完成，下面以增加d作为例子

void ADD(int x, int d, int n){
    while(x <= n){
        Data[x] += d;
        x += lowbit(x);
    }
}

如果需要查询，那么是从后往前一个个相加

int SUM(int x){
    int ans = 0;
    while(x > 0){
        ans += Data[x];
        x -= lowbit(x); 
    }
    return ans;
}

总结

不用细想，树状数组利用了二进制的特殊性质，主要是神奇的lowbit函数，利用数组下标对应的二进制快速的修改相关数组元素，数组对应位置元素可以参考线段树理解
树状数组与线段树相比，编程难度大大降低，代码量大大减少，如果准确理解好了使用起来很方便，但是树状数组能够解决的，线段树也能够解决，但是线段树可以记录一些特殊的东西，比如lazytag等，所以如果问题比较复杂，应该使用线段树而非树状数组

例题

模板1

点修改，区间查询问题。用树状数组维护前缀和，有
$X_N = sum_{i=1}^{N}X_i$
如果想知道X_x到X_y和是多少，只需要用
$sum_{i=1}^{y}X_i-sum_{i=1}^{x-1}X_i$

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int MAXN = 1e6 + 100;
const double eps = 1e-6;
int Data[MAXN];
int Pre[MAXN];
int lowbit(int x){
    return x & -x;
}
void ADD(int x, int n, int d){
    while(x <= n){
        Pre[x] += d;
        x += lowbit(x);
    }
}
int SUM(int x){
    int ans = 0;
    while(x > 0){
        ans += Pre[x];
        x -= lowbit(x); 
    }
    return ans;
}
int main(){
    int n, m, x, y, op, k;
    cin>>n>>m;
    for(int i=0;i<n;i++){
        cin>>Data[i];
        if(i == 0){
            ADD(i + 1, n, Data[i]);
        }else ADD(i + 1, n, Data[i] - Data[i - 1]);
    }
    while(m--){
        cin>>op;
        if(op == 1){
            cin>>x>>y>>k;
            ADD(x, n, k);
            ADD(y + 1, n, -k);
        }else{
            cin>>x;
            cout<<SUM(x)<<'n';
        }
    }
    return 0;
}

模板2

区间修改，点查询。此类问题需要使用树状数组维护一个差分数组，所谓差分数组，就是根据原来的数组构造的一个新的数组，这个数组的每一个元素都是原来相应位置的元素减去他前一个元素所得到的数，第一个位置不变。
如果用数学语言描述，设a为原数组，b为差分数组，那么有
$b_i=left{ begin{array}{c} a_i&i=1\ a_i-a_{i-1}&i>1end{array}right.$
可以想见，假设我们对原来的数组进行在某个区间段内加上一个数d，差分数组应该有什么变化呢？显然第一个发生改变的位置的元素比之前大d，最后一个发生改变的位置的后一个元素比之前少d，那么我们就将区间修改成功转换成两个单点修改，在查询的时候只需要求出差分数组的前缀和即可，而树状数组维护的正是前缀和

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int MAXN = 1e6 + 100;
const double eps = 1e-6;
int Data[MAXN];
int Pre[MAXN];
int lowbit(int x){
    return x & -x;
}
void ADD(int x, int n, int d){
    while(x <= n){
        Pre[x] += d;
        x += lowbit(x);
    }
}
int SUM(int x){
    int ans = 0;
    while(x > 0){
        ans += Pre[x];
        x -= lowbit(x); 
    }
    return ans;
}
int main(){
    int n, m, x, y, op, k;
    cin>>n>>m;
    for(int i=0;i<n;i++){
        cin>>Data[i];
        if(i == 0){
            ADD(i + 1, n, Data[i]);
        }else ADD(i + 1, n, Data[i] - Data[i - 1]);
    }
    while(m--){
        cin>>op;
        if(op == 1){
            cin>>x>>y>>k;
            ADD(x, n, k);
            ADD(y + 1, n, -k);
        }else{
            cin>>x;
            cout<<SUM(x)<<'n';
        }
    }
    return 0;
}

逆序数

逆序数是线性代数里面的一个概念，首先规定一个标准次序，比方说规定从小到大是标准次序，如果有i<j但a_i>a_j，那么就说这两个数构成一个逆序，在一个序列中所有的这样的逆序加在一起的总数就是这个序列的一个逆序数
求解逆序数有两种方法，归并排序和树状数组，这里使用后者。关于前者的做法在这里
树状数组的解法思想是这样的，设置一个数组记录每个数字出现次数，利用树状数组维护这个数组的前缀和，同时更新逆序数（加上前缀和）这样操作下去可以得到答案
但是这样做的问题是如果一个数非常大，那么数组下标就不能表示，这时候可以考虑离散化的方法，也就是使用一个结构体存储数字和下标，这样需要一个排序操作，因为可能出现重复数字，所以排序应先按照value，再按照下标顺序
例题

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int MAXN = 1e6 + 100;
const double eps = 1e-6;
int Data[MAXN];
int n;
struct number{
    int id;
    int value;
}num[MAXN];
int lowbit(int x){
    return x & -x;
}
ll sum(int x){
   ll ans = 0;
   while(x > 0){
       ans += Data[x];
       x -= lowbit(x);
   } 
   return ans;
}
void ADD(int x){
    while(x <= n){
        Data[x]++;
        x += lowbit(x);
    }
}
int main(){
    scanf("%d", &n);
    for(int i=1;i<=n;i++){
        num[i].id = i;
        scanf("%d", &num[i].value);
    }sort(num + 1, num + 1 + n, [](number x, number y){
        if(x.value == y.value) return x.id < y.id;
        return x.value < y.value;
    });
    ll ans = 0;
    for(int i=1;i<=n;i++){
        ADD(num[i].id);
        ans += i - sum(num[i].id);
    }printf("%lld", ans);
    return 0;
}