概述
当我们需要用到数组来存放数据并对数据进行操作时，往往有这么几种数组形式：
1.普通数组：
修改操作：令 a[x]+=k ，时间复杂度O(1)
询问操作：输出a[x]+a[x+1]+a[x+2]+…+a[y-1]+a[y] ，时间复杂度O(n)
2.前缀和数组：
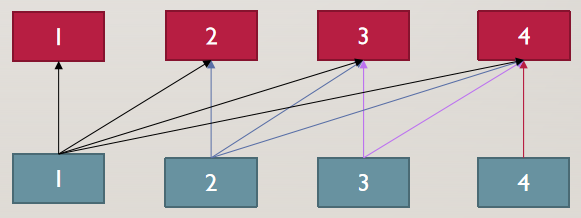
查询操作：直接输出a[y] - a[x-1]就好了，时间复杂度O(1)
修改操作：对于所有大于等于x的y，都要让a[y]+=k，时间复杂度O(n)；
综上我们发现，两种方法，要么修改极快，查询极慢，要么修改极慢，查询极快 为什么会这样呢？因为我们用的两种数据结构不够优秀。因此我们便引入树状数组来均衡两种数组的特性。
首先要知道什么是树状数组：
如图
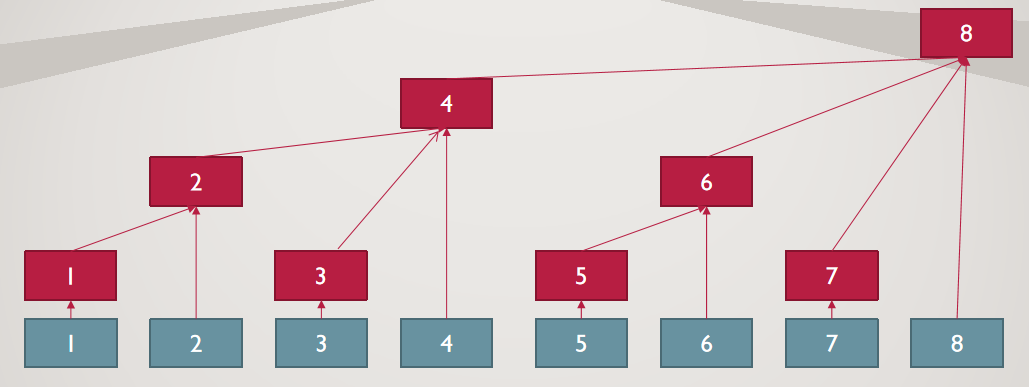
蓝色方块是原数列的对应元素，可以发现每一个红色方块都是一段连续的蓝色方块的和 ，红色方块存放的就是树状数组。
那么我们怎么确定树状数组每一位存放的是那一段原数列的和呢？
首先我们可以发现，该段原数列的右端点都是其对应的原数列的位置，那么只需要确定其左端点即可；
左端点的确定过程需要用二进制来解释：假设该位置为第n位，m是n对应的二进制，那么该点存放的区间的左端点对应的二进制是把m中位数最小的一个1变为0，然后加1；比如如果n = 6，那么就化为 n=m = 110，将m的最靠右的1变为0，得到 m1=100，则左端点为m1+1=101=5。
既然我们已经知道了这一性质，那么该如何运算呢？
我们可以通过n&(-n)这一操作来得到m最小位的1表示的大小，所以左端点可以表示为n-n&(-n)+1。
然后我们就可以构建树状数组了！（上代码）
#include<bits/stdc++.h>
using namespace std;
int n,m;
int action,x,y;
const int maxn=1e7+10;
int tree[maxn]={0};
int a[maxn];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
tree[i]=a[i];
for(int j=i-(i&(-i))+1;j<=i-1;j++){ //构建树状数组
tree[i]+=a[j];
}
}构建完成树状数组，我们就要对其进行操作（不然构建它干啥）
首先看两个基本操作：
1.单点修改：
由树状数组的性质可以得到，如果我们要对原数组中某一点的值进行修改（以加上一个数为例），就要不断找到该位置的父节点然后加上同一个数。
那么怎么找到其父节点呢？我们发现n+n&(-n)就是其父节点。（直接上代码）
for(int i=1;i<=m;i++){
cin>>action>>x>>y;
if(action==1){
for(int j=x;j<=n;j+=j&(-j)){ //单点修改，不断找其父节点，加上同一个数
tree[j]+=y;
}
continue;
}复杂度位O(logn）。
2.区间求和
假设我们要求的区间左端点为l，右端点为n，那么区间求和可以看作是前n项求和减去前l项求和；
关于树状数组求前n项的和可以将其拆分为几部分；如：100010010可以将其拆分为100000000+10000+10，而经过分析可发现，这三个数对应的树状数组中的节点之和正好为前100010010项的和，所以我们只要将这三个节点相加即可（得到三个节点的方法在上文中已经给出，所以我们直接上代码）
if(action==2){
int a=0,b=0;
for(int j=x-1;j>0;j-=j&(-j)){ //区间求和，将区间拆分成多个区间的和
a+=tree[j];
}
for(int j=y;j>0;j-=j&(-j)){
b+=tree[j];
}
cout<<b-a<<endl; //前y项的和减去前x项的和就是区间（x，y）的和。
}时间复杂度为O(logn)。
三部分总代码：
#include<bits/stdc++.h>
using namespace std;
int n,m;
int action,x,y;
const int maxn=1e7+10;
int tree[maxn]={0};
int a[maxn];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
tree[i]=a[i];
for(int j=i-(i&(-i))+1;j<=i-1;j++){ //构建树状数组
tree[i]+=a[j];
}
}
for(int i=1;i<=m;i++){
cin>>action>>x>>y;
if(action==1){
for(int j=x;j<=n;j+=j&(-j)){ //单点修改，不断找其父节点，加上同一个数
tree[j]+=y;
}
continue;
}
if(action==2){
int a=0,b=0;
for(int j=x-1;j>0;j-=j&(-j)){ //区间求和，将区间拆分成多个区间的和
a+=tree[j];
}
for(int j=y;j>0;j-=j&(-j)){
b+=tree[j];
}
cout<<b-a<<endl; //前y项的和减去前x项的和就是区间（x，y）的和。
}
}
return 0;
} 练习请转到：
【模板】树状数组 1 - 洛谷https://www.luogu.com.cn/problem/P3374
那么到这里树状数组的基础功能我们都看完了，它还有几个进阶功能，需要我们在基础功能之上进行灵活变通。
3.区间修改和单点查询
如果单纯的对原数组的树状数组进行区间求和，不难看出这是一件复杂度爆炸的事情；所以我们不妨对原数组求其差分数组，然后对差分数组建立树状数组，那么区间修改就变为了对差分数组的左右端点的两次单点修改，是不是就快多了呢？
同样，单点查询就可以看作是对差分数组的区间求和，这样又转换成了最基本的树状数组操作问题。（上代码）
#include<bits/stdc++.h>
using namespace std;
const long long maxn=500050;
long long a[maxn]={0},b[maxn],tree[maxn]={0};
long long n,m;
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
b[i]=a[i]-a[i-1]; //b是差分数组，求b的树状数组可以将区间修改变为两次单点修改，将单点查询改为一次区间求和
tree[i]=b[i];
for(int j=i-(i&(-i))+1;j<=i-1;j++){ //构建树状数组
tree[i]+=b[j];
}
}
for(int i=1;i<=m;i++){
int op;
cin>>op;
if(op==1){
long long x,y,k;
cin>>x>>y>>k;
for(int j=x;j<=n;j+=j&(-j)){
tree[j]+=k;
}
for(int j=y+1;j<=n;j+=j&(-j)){ //两次单点修改
tree[j]-=k;
}
continue;
}
if(op==2){
long long x;
cin>>x;
int ans=0;
for(int j=x;j>0;j-=j&(-j)){ //区间求和，将区间拆分成多个区间的和
ans+=tree[j];
}
cout<<ans<<endl;
continue;
}
}
return 0;
}具体问题：
【模板】树状数组 2 - 洛谷https://www.luogu.com.cn/problem/P3368
4.区间求和和区间查询：
此时的区间查询我们只好看作是多次单点查询，有了上一问题的经验，我们知道这一问题也要用差分数组来解决；
至于区间求和，在树状数组中它变成了什么呢？
没错！变成了求差分数组b的前缀和的前缀和！ 也就是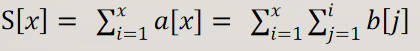
交换求和顺序，得到：
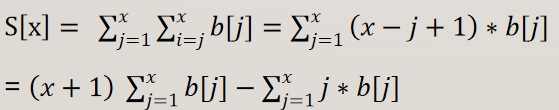
故答案变为了 ：
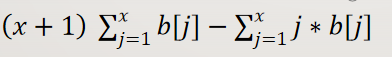
前一部分维护数组b的树状数组可以解决；
设数组c有c[i] = i*b[i]，维护数组c的树状数组可以解决后一部分。（话不多说，直接上代码）
#include<bits/stdc++.h>
using namespace std;
const long long maxn=500050;
long long a[maxn]={0},b[maxn],c[maxn],tree[maxn]={0},tree2[maxn]={0};
long long n,m;
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
b[i]=a[i]-a[i-1];//b是差分数组，求b的树状数组可以将区间修改变为两次单点修改，将单点查询改为一次区间求和
c[i]=i*b[i];
tree[i]=b[i];
tree2[i]=c[i];
for(int j=i-(i&(-i))+1;j<=i-1;j++){ //构建树状数组
tree[i]+=b[j];
tree2[i]+=c[j];
}
}
for(int i=1;i<=m;i++){
int op;
cin>>op;
if(op==1){
long long x,y,k;
cin>>x>>y>>k;
for(int j=x;j<=n;j+=j&(-j)){
tree[j]+=k;
tree2[j]+=k*x;
}
for(int j=y+1;j<=n;j+=j&(-j)){ //两次单点修改
tree[j]-=k;
tree2[j]-=k*(y+1);
}
continue;
}
if(op==2){
long long x,y;
cin>>x>>y;
long long a1=0,a2=0,b1=0,b2=0;
for(int j=x-1;j>0;j-=j&(-j)){ //区间求和，将区间拆分成多个区间的和
a1+=tree[j];
//cout<<a1<<endl;
}
for(int j=x-1;j>0;j-=j&(-j)){ //区间求和，将区间拆分成多个区间的和
a2+=tree2[j];
//cout<<a2<<endl;
}
for(int j=y;j>0;j-=j&(-j)){ //区间求和，将区间拆分成多个区间的和
b1+=tree[j];
//cout<<b1<<endl;
}
for(int j=y;j>0;j-=j&(-j)){ //区间求和，将区间拆分成多个区间的和
b2+=tree2[j];
//cout<<b2<<endl;
}
cout<<(y+1)*b1-b2-((x)*a1-a2)<<endl;
continue;
}
}
return 0;
}具体问题：
【模板】线段树 1 - 洛谷https://www.luogu.com.cn/problem/P3372
如果看懂了，希望点个赞支持一下 ！
最后
以上就是粗暴柜子为你收集整理的树状数组及其应用 1.普通数组：2.前缀和数组：综上我们发现，两种方法，要么修改极快，查询极慢，要么修改极慢，查询极快 为什么会这样呢？因为我们用的两种数据结构不够优秀。因此我们便引入树状数组来均衡两种数组的特性。首先要知道什么是树状数组： 1.单点修改：2.区间求和3.区间修改和单点查询4.区间求和和区间查询：如果看懂了，希望点个赞支持一下 ！的全部内容，希望文章能够帮你解决树状数组及其应用 1.普通数组：2.前缀和数组：综上我们发现，两种方法，要么修改极快，查询极慢，要么修改极慢，查询极快 为什么会这样呢？因为我们用的两种数据结构不够优秀。因此我们便引入树状数组来均衡两种数组的特性。首先要知道什么是树状数组： 1.单点修改：2.区间求和3.区间修改和单点查询4.区间求和和区间查询：如果看懂了，希望点个赞支持一下 ！所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复