「树状数组」第 1 节：树状数组能解决的问题第 1 节树状数组能解决的问题

60 阅读 0 评论 40 点赞

我是靠谱客的博主舒适蜗牛，最近开发中收集的这篇文章主要介绍「树状数组」第 1 节：树状数组能解决的问题第 1 节树状数组能解决的问题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

关键词：位运算、前缀和的查询与更新。

第 1 节树状数组能解决的问题

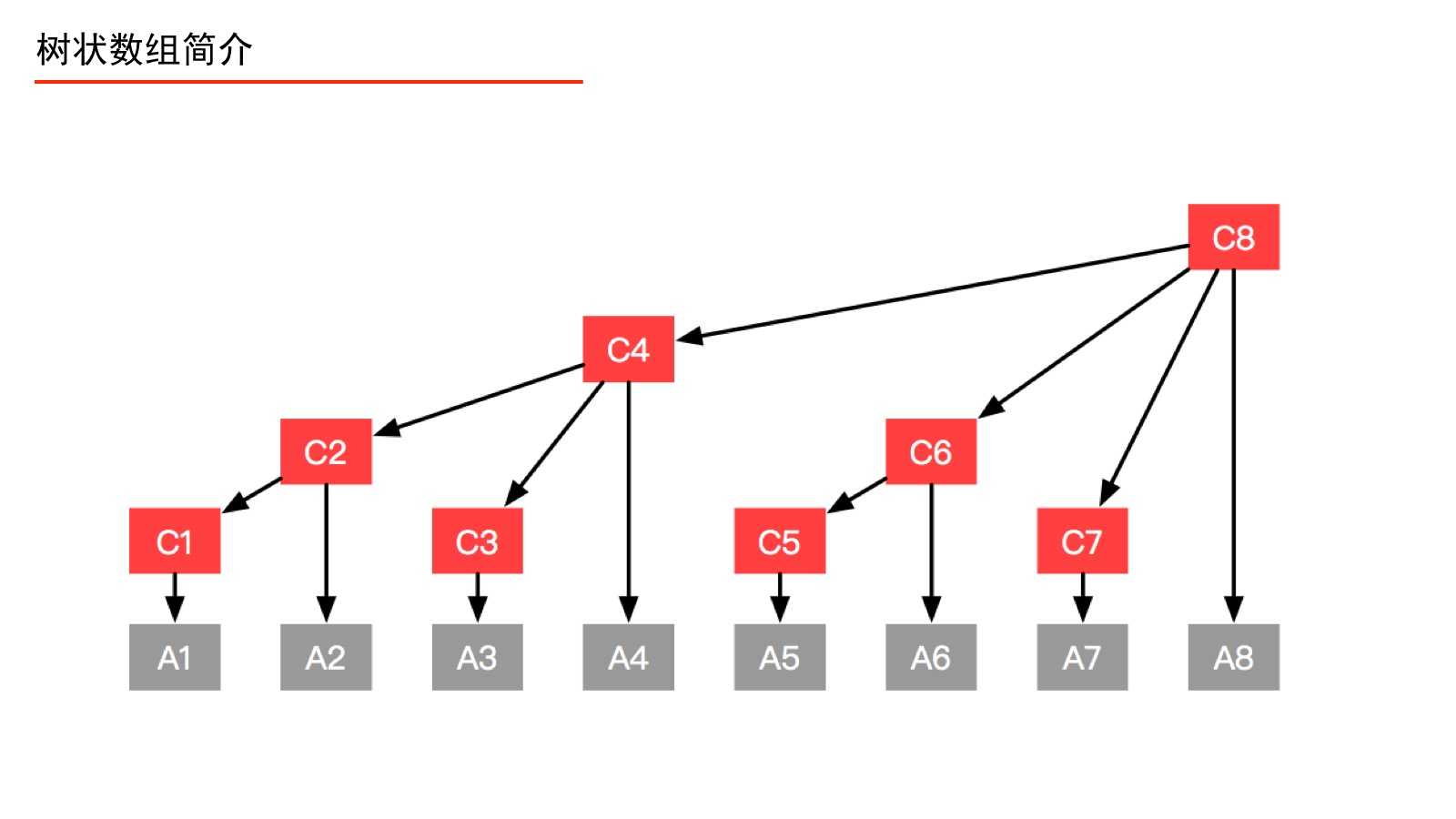
树状数组，也称作「二叉索引树」（Binary Indexed Tree）或 Fenwick 树。
它能高效地实现下面两个操作：

数组的「前缀和」查询；
数组的「单点更新」。

在这里插入图片描述

下面具体解释这两个操作。

数组的「前缀和」查询

首先看下面这个例子，了解什么是数组的前缀和查询。

例 1

已知数组 arr = [10, 15, 17, 19, 20, 14, 12]，求下标 0 至下标 4 的所有元素的和。
分析：

「前缀和」定义了一个数组从「头」开始的区间，计算的是从下标位置是 0 开始的区间内的所有元素的和；
注意：理解「前缀」的意思，下标位置必须从 0 开始计算；
其它不是从 0 开始的数组的区间和可以转化成前面的这个问题。

解：在 Python 语言中，可以使用 sum(arr[0:5]) 得到下标 0 至下标 4 的所有元素的和。
说明：在 Python 的语法中，切片操作不包括结下标的数值，因此 arr[0:5]=[arr[0], arr[1], arr[2], arr[3], arr[4]]。

数组的「单点更新」

例 2

已知数组 [10, 15, 17, 19, 20, 14, 12] 。

将下标为 4 的元素增加 2；
将下标为 6 的元素减少 3。

分析：

给出这个例题只是为了让大家熟悉这个提法，「单点更新」并不关心这个数「变成了什么」，它的提法是给出一个数变化了多少，因为增加一个数等价于减去这个数的相反数，因此以上两个提法其实可以合并成：将某个下标的元素增加多少；
如果我们不使用任何任何数据结构，仅依靠定义，「单点更新」操作的时间复杂度是 $O (1)$ ，数组的「前缀和」查询的时间复杂度是 $O (n)$ ，要扫描这个区间的一大部分元素，才能得到这个区间的和。优化的做法是：先计算出一个“前缀和”数组，这个数组的每个元素的值对应的正是原来数组的前缀和。

例 3

已知数组 arr = [1, 2, 3, 4, 5, 6, 7]，计算「前缀和」数组 cumsum(arr)。

分析：根据「前缀和」的定义，容易计算出前缀和数组是 cumsum(arr) = [1, 3, 6, 10, 15, 21, 28]。
Python 代码：

arr = [1, 2, 3, 4, 5, 6, 7]
cumsum = [0] * len(arr)
cumsum[0] = arr[0]
for i in range(1, len(arr)):
    cumsum[i] = cumsum[i - 1] + arr[i]
print(cumsum)

有了「前缀和」数组以后，每次查询「前缀和」的时间复杂度变成了 $O (1)$ ，此时计算「区间和」就容易了。

例 4

已知数组 arr = [1, 2, 3, 4, 5, 6, 7] ，求第 3 个元素到第 7 个元素（包括第 7 个元素）的和。

分析：

第 3 个元素到第 7 个元素（包括第 7 个元素）的和可以表示为 sum(arr[2:7])；
注意：第几个元素与下标的序号有一个位置的偏移，并且 Python 中的切片不包含结尾端点）；
我们假设我们有了「前缀和」数组，就可以以 $O (1)$ 时间复杂度完成这个问题。
第 1 个元素到第 7 个元素（包括第 7 个元素）的和可以表示成：

cumsum(arr[0:7]) = nums[0] + nums[1] + nums[2] + nums[3] + nums[4] + nums[5] + nums[6]

第 1 个元素到第 2 个元素（包括第 2 个元素）的和可以表示成：

cumsum(arr[0:2]) = nums[0] + nums[1]

于是第 3 个元素到第 7 个元素（包括第 7 个元素）的和：

sum(arr[2:7]) = cumsum(arr[0:7]) - cumsum(arr[0:2])

那么问题来了：执行「单点更新」操作，就得更新「前缀和」数组又得计算一次前缀和，时间复杂度为 $O (n)$ 。那如果一次业务场景中计算「前缀和」和「单点更新操作」的次数都很多，使用「前缀和」数组就不高效了。而 Fenwick 树就是一个实现了快速计算「前缀和」和「单点更新」操作这两个操作的数据结构。

（本节完）