$树状数组详解$

先来看几个问题吧。

1. 什么是树状数组？

顾名思义，就是用数组来模拟树形结构呗。那么衍生出一个问题，为什么不直接

建树？答案是没必要，因为树状数组能处理的问题就没必要建树。和 $Trie$ 树的构造

方式有类似之处。

2. 树状数组可以解决什么问题

可以解决大部分基于区间上的更新以及求和问题。

3. 树状数组和线段树的区别在哪里

树状数组可以解决的问题都可以用线段树解决，这两者的区别在哪里呢？树状数

组的系数要少很多，就比如字符串模拟大数可以解决大数问题，也可以解决 $1+$

$1$ 的问题，但没人会在 $1+1$ 的问题上用大数模拟。

4. 树状数组的优点和缺点

修改和查询的复杂度都是 $O(logN)$ ，而且相比线段树系数要少很多，比传统数

组要快，而且容易写。

• 缺点是遇到复杂的区间问题还是不能解决，功能还是有限。

$LOWBIT$

$敲重点！！$

先给出一张图

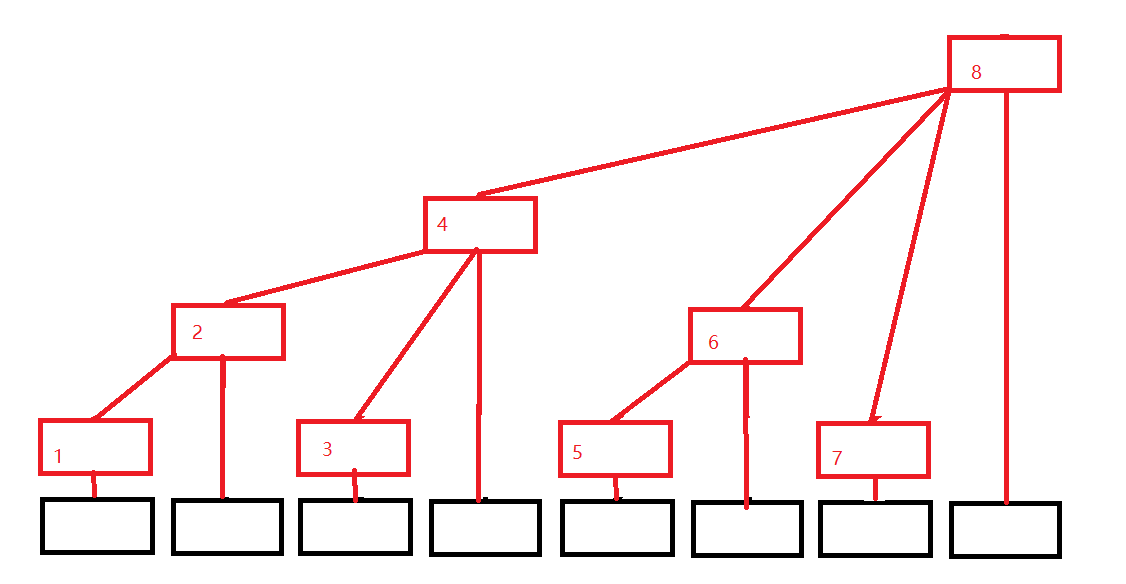
不难得出 ：

• $C[1]=A[1]$
• $C[2]=A[1]+A[2]$
• $C[3]=A[3]$
• $C[4]=A[1]+A[2]+A[3]+A[4]$
• $C[5]=A[5]$
• $C[6]=A[5]+A[6]$
• $C[7]=A[7]$
• $C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]$

可以发现，这颗树是有规律的

$C[i]=A[i-2k+1]+A[i-2k+2]+...+A[i]$ ( $k$ 为 $i$ 的二进制中从最低位到高位连续零的长度 )

那么如何求出二进制中从最低位到高位连续零的长度呢 ？

$2^k=i\&(-i)$

（我也不懂）

简单来说，树状数组其实其实就是把一个数存在它的二进制中为 $1$ 的位中。

每次就找一个数的二进制中最后一个 $1$ 的位置。

例：

$7$ 的二进制为 $00000111$。

则 $7$ 的反码为 $11111001$。

将 $00000111$ 和 $11110111$ 进行按位与得，$00000001$。

$lowbit$的实现

inline int lowbit(int a)
{
    return a & (-a);
}

$一维树状数组$

- 单点修改，区间查询

• 模板
• 单点修改

inline void update(int x, int y)
{
    while (x <= n)
    {
        c[x] += y;
        x += lowbit(x);
    }
}

• 区间查询
  要想求出 $x\to y$ 相当于 $1\to y$ 减去 $1\to (x-1)$

inline int query(int x)
{
    int ans = 0;
    while (x)
    {
        ans += c[x];
        x -= lowbit(x);
    }
    return ans;
}

故 ，

修改 ： $update(x,val)$

查询 ： $query(y)-query(x-1)$

$ACcode$

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 1e6 + 5;
int n, q, a[maxn], c[maxn];
inline int lowbit(int a)
{
    return a & (-a);
}
inline void update(int x, int y)
{
    while (x <= n)
    {
        c[x] += y;
        x += lowbit(x);
    }
}
inline int query(int x)
{
    int ans = 0;
    while (x)
    {
        ans += c[x];
        x -= lowbit(x);
    }
    return ans;
}
signed main()
{
    cin >> n >> q;
    for (int i = 1; i <= n; i++)
        cin >> a[i], update(i, a[i]);
    for (int i = 1; i <= q; i++)
    {
        int x, y, z;
        cin >> x >> y >> z;
        if (x == 1)
        {
            update(y, z);
        }
        else
        {
            cout << query(z) - query(y - 1) << endl;
        }
    }
    return 0;
}

- 区间修改，单点查询

• 模板

• 处理

  先弄个差分树状数组

  update(i, a[i] - a[i - 1]);
  

• 区间修改

  利用前缀和的特性来 $O(1)$ 更新区间的值。

  当区间 $[l,r]$ 加上 $k$ 时，$a[l]$ 与 $a[l-1]$ 的差增加了 $k$，$a[r+1]$ 与 $a[r]$ 的差减少了 $k$

  inline void update(int x, int y)
  {
  	while (x <= n)
  	{
      	c[x] += y;
      	x += lowbit(x);
  	}
  }
  inline void add(int l, int r, int x)
  {
  	update(l, x);
  	update(r + 1, -x);
  }
  

• 单点查询

  inline int query(int x)
  {
  	int ans = 0;
  	while (x)
  	{
      	ans += c[x];
      	x -= lowbit(x);
  	}
  	return ans;
  }
  

故 ，

修改 ： $update(l,x)update(r+1,-x)$

查询 ： $query(x)$

$ACcode$

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 1e6 + 5;
int n, q, a[maxn], maxx, c[maxn];
inline int lowbit(int a)
{
    return a & (-a);
}
inline void update(int x, int y)
{
    while (x <= n)
    {
        c[x] += y;
        x += lowbit(x);
    }
}
inline void add(int l, int r, int x)
{
    update(l, x);
    update(r + 1, -x);
}
inline int query(int x)
{
    int ans = 0;
    while (x)
    {
        ans += c[x];
        x -= lowbit(x);
    }
    return ans;
}
signed main()
{
    cin >> n >> q;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        update(i, a[i] - a[i - 1]);
    }
    for (int i = 1; i <= q; i++)
    {
        int abc, x, y, z;
        cin >> abc;
        if (abc == 1)
        {
            cin >> x >> y >> z;
            add(x, y, z);
        }
        else
        {
            cin >> x;
            cout << query(x) << endl;
        }
    }
    return 0;
}

- 区间修改，区间查询

树状数组 ：区间修改，区间查询

华丽的结束线

不 ， 没完

$二维树状数组$

1.单点修改，区间查询

查询时要用到容斥原理

$ACcode$

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 5001;
int n, m;
int tree[maxn][maxn];
int lowbit(int x)
{
    return x & -x;
}
/
void update(int x, int y, int z)
{
    for (int i = x; i <= n; i += lowbit(i))
    {
        for (int j = y; j <= m; j += lowbit(j))
        {
            tree[i][j] += z;
        }
    }
}
int query(int x, int y)
{

    int res = 0;
    for (int i = x; i; i -= lowbit(i))
    {
        for (int j = y; j; j -= lowbit(j))
        {
            res += tree[i][j];
        }
    }
    return res;
}
/
signed main()
{
    cin >> n >> m;
    int op;
    while (scanf("%lld", &op) != EOF)
    {
        int a, b, c, d;
        cin >> a >> b >> c;
        if (op == 1)
        {
            update(a, b, c);
        }
        else
        {
            cin >> d;
            cout << query(c, d) - query(a - 1, d) - query(c, b - 1) + query(a - 1, b - 1) << endl;
        }
    }
}

2. 区间修改，单点查询

这里也需要用到差分 （二维啊！！！）

差分数组 $d[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]$

$部分代码$

void update(int x, int y, int k)
{
    for (int i = x; i <= n; i += lowbit(i))
    {
        for (int j = y; j <= m; j += lowbit(j))
        {
            t[i][j] += k;
        }
    }
}

void range_update(int a, int b, int c, int d, int k)
{
    update(a, b, k);
    update(a, d + 1, -k);
    update(c + 1, b, -k);
    update(c + 1, d + 1, k);
}

3. 区间修改，区间查询

下面这个式子表示的是点(x, y)的二维前缀和：

${\sum }_{i=1}^x{\sum }_{j=1}^y{\sum }_{k=1}^i{\sum }_{h=1}^{j}d[h][k]$

时间复杂度 $O(lo{g}_{2}n)$

接下来统计一下每个 $d[h][k]$ 出现过多少次。$d[1][1]$ 出现了 $x\times y$次，$d[1][2]$出

现了 $x\times (y-1)$ 次

……

$d[h][k]$出现了 $(x-h+1)\ast (y-k+1)$ 次。

那么这个式子就可以写成：

${\sum }_{i=1}^x{\sum }_{j=1}^{y}d[i][j]\times (x+1-i)\ast (y+1-j)$

把这个式子展开，就得到：

$(x+1)\times (y+1)\times {\sum }_{i=1}^x{\sum }_{j=1}^{y}d[i][j]-(y+1)\times {\sum }_{i=1}^x{\sum }_{j=1}^{y}d[i][j]\times i-(x+1)\times {\sum }_{i=1}^x{\sum }_{j=1}^{y}d[i][j]\times j+{\sum }_{i=1}^x{\sum }_{j=1}^{y}d[i][j]\times i\times j$

那么我们要开四个树状数组，分别维护：

$d[i][j],d[i][j]\times i,d[i][j]\times j,d[i][j]\times i\times j$

$\mathcal{E}\mathcal{N}\mathcal{D}$

最后

以上就是传统玉米为你收集整理的树状数组详解 树 状 数 组 详 解 树状数组详解 树状数组详解 的全部内容，希望文章能够帮你解决树状数组详解 树 状 数 组 详 解 树状数组详解 树状数组详解 所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。