C++迭代加深搜索及其例题讲解—————Addition Chains

74 阅读 0 评论 49 点赞

我是靠谱客的博主大力饼干，最近开发中收集的这篇文章主要介绍C++迭代加深搜索及其例题讲解—————Addition Chains，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

前言：

学习算法时，一个关键的问题是什么时候来使用它。在一些搜索问题中，使用普通的DFS可能会让你把时间浪费在深度非常大而且答案不是最优的搜索过程上，甚至有的时候DFS搜索的深度是无穷的，而BFS虽说理论上可以避免这种情况，却又无法满足题目的某些需求，或者无法实现。仔细思考一下这个例子，它有着两个特征：一是它是个最优解问题，二是最优的答案深度最小，如右图：

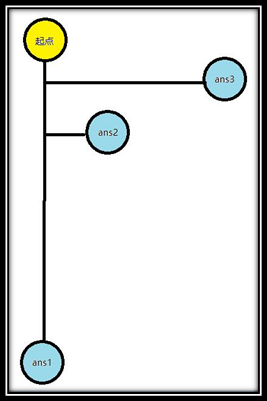
但是我们的答案有三个，若我们要ans3这个答案，那么DFS和BFS都是不满足的，so我们引入迭代加深搜索来解决这个问题。

概念：

1.迭代加深搜索，实质上就是限定下界的深度优先搜索。即首先允许深度优先搜索K层搜索树，若没有发现可行解，再将K+1后重复以上步骤搜索，直到搜索到可行解。

2.在迭代加深搜索的算法中，连续的深度优先搜索被引入，每一个深度约束逐次加1，直到搜索到目标为止。

3.迭代加深搜索算法就是仿广度优先搜索的深度优先搜索。既能满足深度优先搜索的线性存储要求，又能保证发现一个最小深度的目标结点。

4.从实际应用来看，迭代加深搜索的效果比较好，并不比广度优先搜索慢很多，但是空间复杂度却与深度优先搜索相同，比广度优先搜索小很多，在一些层次遍历的题目中，迭代加深不失为一种好方法！

那么我们就开始例题吧。

题目描述：

An addition chain for n is an integer sequence <a0, a1,a2,...,am> with the following four properties:

a0 = 1
am = n
a0 < a1 < a2 < ... < am-1 < am
For each k (1 <= k <= m) there exist two (not necessarily different) integers i and j (0 <= i, j <= k-1) with ak = ai + aj

You are given an integer n. Your job is to construct an addition chain for n with minimal length. If there is more than one such sequence, any one is acceptable.

For example, <1, 2, 3, 5> and <1, 2, 4, 5> are both valid solutions when you are asked for an addition chain for 5.

输入;

The input will contain one or more test cases. Each test case consists of one line containing one integer n (1 <= n <= 100). Input is terminated by a value of zero (0) for n.

输出;

For each test case, print one line containing the required integer sequence. Separate the numbers by one blank.

输入样例：

5
7
12
15
77
0

输出样例：

1 2 4 5
1 2 4 6 7
1 2 4 8 12
1 2 4 5 10 15
1 2 4 8 9 17 34 68 77

总之就是：

已知一个数列a0，a1，……，am（其中a0=1，am=n，a0<a1<……<am-1<am）。

对于每个k，需要满足ak=ai+aj（0 ≤ i，j ≤ k-1，这里i与j可以相等）。

现给定n的值，要求m的最小值（并不要求输出）。

及这个数列每一项的值（可能存在多个数列，只输出任一个满足条件的就可以了）（~~但其实不然~~）。

思路分析:

此是来自GM的题解：

首先可以求出最少需要几个元素可以达到n。按照贪心的策略，对于每个元素的值，都选择让它等于一个数的两倍，即对于每个Ai = Ai-1 + Ai-1, 当Ai>=n时就跳出循环，得到最少元素个数。然后从最少步数开始迭代加深搜索。最后再用上一些减枝技巧即可。

而现在是主要讲IDDFS。

首先，当长度与规定深度相同时，我们就要判断数列末项是否相同，如果相同就是答案。

然后从数列的前项里求最好的方法。（这里一定要~~从后往前找，不然过不了~~）。

然后还有一个期望函数，若果用最大的数都无法得到答案，那么就返回。

代码实现：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int n,ans[105];
bool f;
void dfs(int x,int de)
{
	if(f)
		return;
	if(x==de)
	{
		if(ans[x]==n)
			f=1;
		return;
	}
	for(int i=x;i>=0;i--)
	{
		for(int j=i;j<=x;j++)
			if(ans[i]+ans[j]>ans[x]&&ans[i]+ans[j]<=n)
			{
				int sum=ans[i]+ans[j];
				for(int k=x+2;k<=de;k++)
					sum*=2;
				if(sum<n)
					continue;
				ans[x+1]=ans[i]+ans[j];
				dfs(x+1,de);
				if(f)
					return;
			}
	}
}
int main()
{
	while(scanf("%d",&n)!=-1)
	{
	    if(n==0)
            return 0;
		memset(ans,0,sizeof(ans));
		f=0;
		ans[0]=1;
		int m=1,depth=0;
		while(m<n)
		{
			m*=2;
			depth++;
		}
		while(1)
		{
			dfs(0,depth);
			if(f)
				break;
			depth++;
		}
		printf("%d",ans[0]);
		for(int i=1;i<=depth;i++)
			printf(" %d",ans[i]);
		printf("n");
	}
}