DFS(爆搜、深搜)

DFS俗称爆搜，深搜。DFS对应的流程是一个树的结构，DFS的精髓在于递归求解的思路以及回溯的处理。针对搜索的过程，又有重要的剪枝优化。必要的剪枝优化对DFS的顺序执行有很大的作用。

DFS的过程就是沿着树的深度遍历树的节点，尽可能深的搜索树的分支，当节点v的所在边都搜过，搜索回溯到发现节点v的那条边的起始节点。

DFS使用的数据结构是栈，时间复杂度是O(n)，DFS不具有最短性，也就是DFS搜到的路径不一定是最短路。

详细搜索过程点这！！！ 

#include<iostream>
using namespace std;
const int N=10;
int path[N];  //保存序列
bool state[N];//数字是否被用过
int n;
void dfs(int u){
	if(u==n){ //数字全部用完 输出数组
		for(int i=0;i<n;i++) printf("%d ",path[i]);
		printf("n");
		return;
	}
	for(int i=1;i<=n;i++){//空位上可以选择的数字
		if(!state[i]){//数字没有被用过
			path[u]=i;//放入空位中
			state[i]=true;//标记被用过
			dfs(u+1);//填下一个空位
			state[i]=false;//回溯 将数字i取出 并把状态改变
			//path[u]=0;//此句可以不写 因为下次使用时直接把原数据覆盖掉
		}
	}
}
int main(){
	cin>>n;
	dfs(0);  //0代表path数组从0开始存
	return 0;
}

 dfs递归过程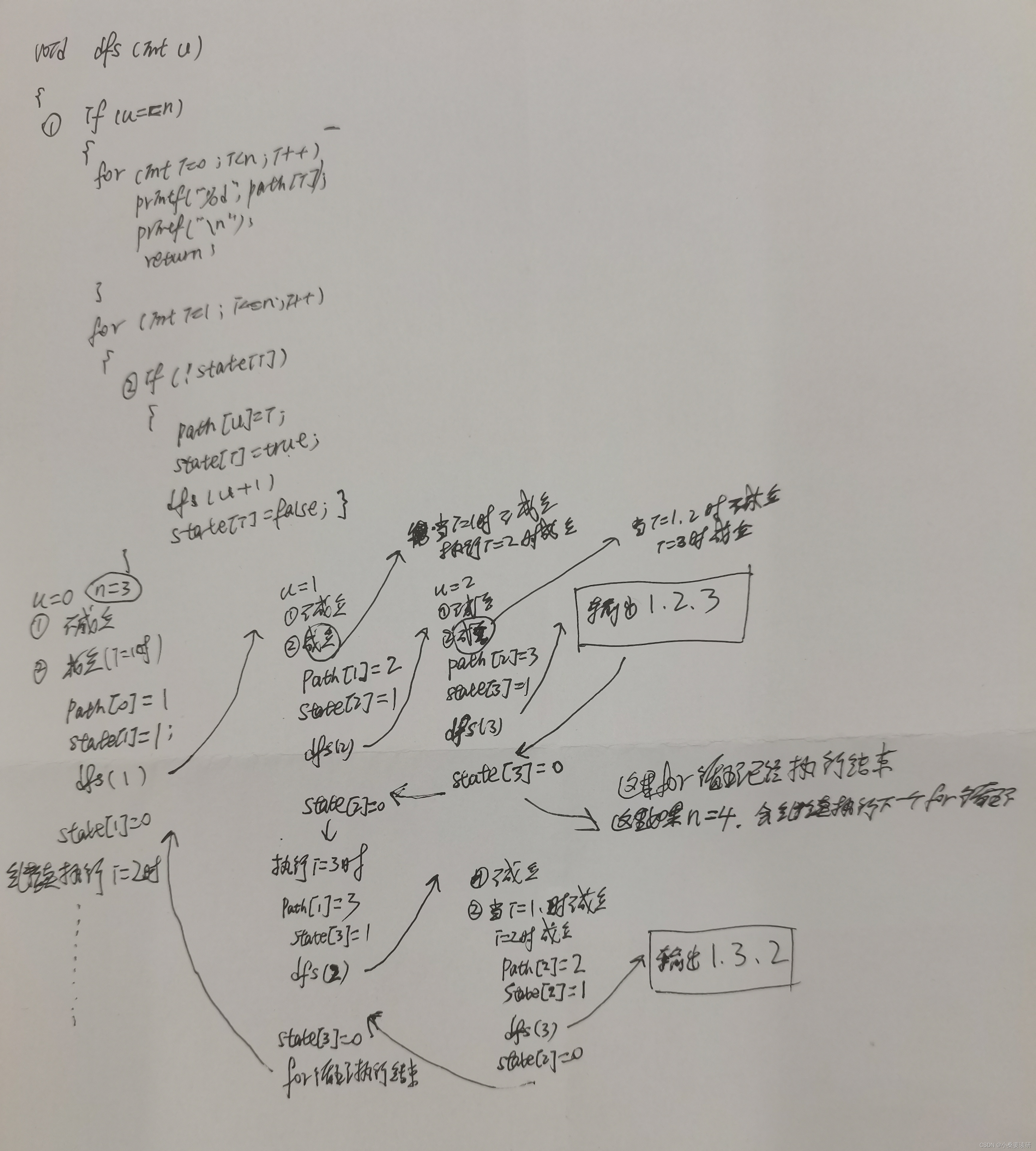

 解析看这！！！

#include<iostream>
using namespace std;
const int N=20;//有对角线 范围乘2
char g[N][N];
bool col[N],dg[N],udg[N];//dg代表对角线 udg代表反对角线
int n;
//已经保证了每行只有一个
void dfs(int u){
	if(u==n){
		for(int i=0;i<n;i++) puts(g[i]);//二维数组可直接输出一行
		puts("");
		return;
	}
	for(int i=0;i<n;i++){
						//i纵坐标 u横坐标  主对角线y=x+b推出b=y-x 为了防止为负 所以加n
						                //反对角线 y=-x+b 推出b=y+x
		if(!col[i]&&!dg[i-u+n]&&!udg[i+u]){
			g[u][i]='Q';
			col[i]=dg[i-u+n]=udg[i+u]=true;
			dfs(u+1);
			col[i]=dg[i-u+n]=udg[i+u]=false;
            g[u][i]='.';
		}
	}
}
int main(){
	cin>>n;
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++)
		g[i][j]='.';//初始值全部赋值位.
	dfs(0);
	return 0;
}

#include<iostream>
using namespace std;
const int N=20;//有对角线 范围乘2
char g[N][N];
bool row[N],col[N],dg[N],udg[N];//dg代表主对角线 udg代表反对角线
int n;
//如果不知道每行都是一个 这个更接近实际
void dfs(int x,int y,int s){ //s表示皇后的个数
	if(y==n) x++,y=0;//该行已经枚举结束
	if(x==n){
		if(s==n){
			for(int i=0;i<n;i++) puts(g[i]);
			puts("");
		}
		return;
	}
	//不放皇后
	dfs(x,y+1,s);
	//放皇后
	if(!row[x]&&!col[y]&&!dg[y-x+n]&&!udg[y+x]){
		row[x]=col[y]=dg[y-x+n]=udg[y+x]=true;
		g[x][y]='Q';
		dfs(x,y+1,s+1);
		g[x][y]='.';
		row[x]=col[y]=dg[y-x+n]=udg[y+x]=false;
	}
}

int main(){
	cin>>n;
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++)
		g[i][j]='.';//初始值全部赋值位.
	dfs(0,0,0);
	return 0;
}

最后

以上就是殷勤咖啡为你收集整理的DFS(爆搜、深搜)的全部内容，希望文章能够帮你解决DFS(爆搜、深搜)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。