[多校 NOIP 联合模拟 20201130 T4] ZZH 的旅行（斜率优化dp，启发式合并，平衡树）题面题解CODE

87 阅读 0 评论 58 点赞

我是靠谱客的博主紧张鞋子，最近开发中收集的这篇文章主要介绍[多校 NOIP 联合模拟 20201130 T4] ZZH 的旅行（斜率优化dp，启发式合并，平衡树）题面题解CODE，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题面

题目背景

因为出题人天天被 ZZH（Zou ZHen）吊打，所以这场比赛的题目中出现了 ZZH 。

简要题面

数据范围

题解

（笔者写两个log的平衡树和启发式合并卡过的，不足为奇）

首先，很容易看出来n^2的做法是个树形DP，而且不是换根DP（笔者想换根DP想了半小时，发现题读难了，唉），

设 dp[i] 为从 i 出发的答案，容易想到这样的状态转移：

$dp_i=max { (a_i-(depth_j-depth_i))cdot b_j + dp_j};,;iin ancestors_j$

（depth是从1到每个点的距离，即深度，ancestors是每个点的祖先集）

怎么办，j 好像要在 i 的子树中枚举？

但是这个式子好像可以推，我们用斜率优化试试：

$begin{matrix} (a_i-(depth_j-depth_i))cdot b_j + dp_j > (a_i-(depth_k-depth_i))cdot b_k + dp_k\ Leftrightarrow (a_i+depth_i)cdot b_j + (dp_j-depth_jcdot b_j) > (a_i+depth_i)cdot b_k + (dp_k-depth_kcdot b_k)\ \ Leftrightarrow Y_j=(dp_j-depth_jcdot b_j);,;Y_k=(dp_k-depth_kcdot b_k);,;X_j=b_j;,;X_k=b_k;,\ (a_i+depth_i)cdot X_j + Y_j > (a_i+depth_i)cdot X_k + Y_k\ Leftrightarrow Y_j-Y_k > (a_i+depth_i)cdot (X_k-X_j) end{matrix}$

这时不妨设 $X_j<X_k$ ，那么：

$Leftrightarrow frac{Y_j-Y_k}{X_j-X_k} < -(a_i+depth_i)$

也就是说，对于 $b_j<b_k$ 的两个决策点 j，k 而言，按照上面的定义把它们抽象成点，若满足上式，则 j 更优，而以下两种情况的 j 肯定不优，可以直接弃掉：

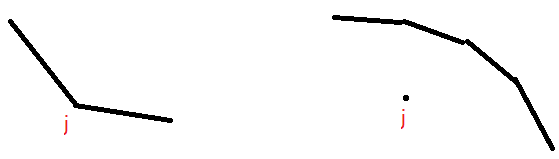
因此，假设这是以 i 为根的子树中的所有点，不包括 i （把它们抽象成点放到平面上）：

我们就要维护这样一个上凸包：

但是呢，这跟朴素的斜率优化不太一样，有以下不同：

$-(a_i+depth_i)$ 无序
新点不一定从两端插入，而有可能从中间插入，这缘于 $X_j(b_j)$ 无序
不一定在序列上跑，而是在树上

第一点其实很好解决，每次从凸包右边开始二分（倍增）就行了。

第二点就有麻烦了，我们得快速在一个凸包内加进一个点。

这种情况，新加的点直接弃掉：

而这种情况两边得分别把下凸的点弃掉：

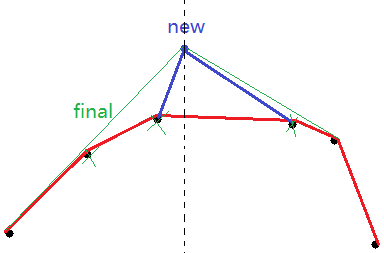
那就硬枚！左边右边分别找最近的点，判断是否下凸，然后丢掉，再判更远的点……

而这些操作，需要支持区间找前驱后继、找左右端点、区间动态加点删点，

于是乎用平衡树维护。

第三点，相当于每个儿子节点有一棵平衡树，把它们并成一棵大树，用启发式合并。

于是插入O(log)，启发式合并O(nlog^2)，二分（倍增）查找（您就别想平衡树上二分了，太麻烦）O(log^2)，总复杂度 O(nlog^2)

CODE

（可见调试得多么累，但是还是没想到会爆long long）

#include<queue>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 1000005
#define LL long long
#define DB double
#define ENDL putchar('n')
#define lowbit(x) ((-x)&(x))
#pragma GCC optimize(2)
LL read() {
	LL f = 1,x = 0;char s = getchar();
	while(s < '0' || s > '9') {if(s=='-')f = -f;s = getchar();}
	while(s >= '0' && s <= '9') {x=x*10+(s-'0');s = getchar();}
	return f * x;
}
const int MOD = 1000000007;
int n,m,i,j,s,o,k;
int a[MAXN],b[MAXN];
//-------------------------------Treap
struct np{int s[2];np(){s[0]=s[1]=0;}np(int A,int B){s[0]=A;s[1]=B;}};
struct tr{
	int s[2];
	int x,siz,hp;
	LL y;
	tr(){x = siz = hp = y = s[0] = s[1] = 0;}
}tre[MAXN];
bool xiatu(int a,int b,int c) {
//	printf("comp %d %d %dn",a,b,c);
	if(a == 0 || c == 0) return 0;
	if(tre[a].x == tre[b].x && tre[a].y >= tre[b].y) return 1;
	if(tre[c].x == tre[b].x && tre[c].y >= tre[b].y) return 1;
	return ((DB)tre[b].y - tre[a].y) / ((DB)tre[b].x - tre[a].x) <= ((DB)tre[c].y - tre[b].y) / ((DB)tre[c].x - tre[b].x);//就是这儿！写乘法爆了35分
}
int CNT;
int newnode(int xi,LL yi) {
	int x = ++ CNT;tre[x] = tr();
	tre[x].siz = 1;tre[x].hp = rand()*114514ll%MOD;
	tre[x].x = xi;tre[x].y = yi;
	return x;
}
int update(int x) {
	tre[x].siz = tre[tre[x].s[0]].siz + tre[tre[x].s[1]].siz + 1;
	tre[0] = tr();return x;
}
np spli(int x,int xi) {
	np as(0,0);
	if(!x) return as;
	int d = (tre[x].x <= xi);
	as = spli(tre[x].s[d],xi);
	tre[x].s[d] = as.s[!d];
	as.s[!d] = update(x);
	return as;
}
np splil(int x) {
	if(!x) return np();
	if(!tre[x].s[0]) {
		int rp = tre[x].s[1];tre[x].s[1] = 0;
		return np(update(x),rp);
	}
	np as = splil(tre[x].s[0]);
	tre[x].s[0] = as.s[1];
	as.s[1] = update(x);
	return as;
}
np splir(int x) {
	if(!x) return np();
	if(!tre[x].s[1]) {
		int lp = tre[x].s[0];tre[x].s[0] = 0;
		return np(lp,update(x));
	}
	np as = splir(tre[x].s[1]);
	tre[x].s[1] = as.s[0];
	as.s[0] = update(x);
	return as;
}
int findp(int x,int rk) {
	if(!x) return 0;
	if(tre[tre[x].s[0]].siz+1 == rk) return x;
	if(tre[tre[x].s[0]].siz+1 < rk)
		return findp(tre[x].s[1],rk - tre[tre[x].s[0]].siz - 1);
	return findp(tre[x].s[0],rk);
}
int merg(int p1,int p2) {
	if(!p1) return p2;if(!p2) return p1;
	if(tre[p1].hp < tre[p2].hp) {
		tre[p1].s[1] = merg(tre[p1].s[1],p2);return update(p1);
	}
	tre[p2].s[0] = merg(p1,tre[p2].s[0]);return update(p2);
}
int ins(int x,int y) {
//	printf("(%d)ins:(%d,%lld)n",x,tre[y].x,tre[y].y);
	if(!x) return y;
	np p = spli(x,tre[y].x);
	np lp = splir(p.s[0]),rp = splil(p.s[1]);
//	printf("%d) (%dn",lp.s[1],rp.s[0]);
	if(xiatu(lp.s[1],y,rp.s[0])) return merg(merg(lp.s[0],lp.s[1]),merg(rp.s[0],rp.s[1]));
	np llp = splir(lp.s[0]);
	while(xiatu(llp.s[1],lp.s[1],y)) {
		lp = llp;llp = splir(lp.s[0]);
	}lp.s[0] = merg(llp.s[0],llp.s[1]);p.s[0] = merg(lp.s[0],lp.s[1]);
	np rrp = splil(rp.s[1]);
//		printf("ok1n");
	while(xiatu(y,rp.s[0],rrp.s[0])) {
//		printf("ok2n");
		rp = rrp;rrp = splil(rp.s[1]);
	}
	rp.s[1] = merg(rrp.s[0],rrp.s[1]);p.s[1] = merg(rp.s[0],rp.s[1]);
//	printf("OK(%d,%d,%d)n",tre[p.s[0]].siz,tre[y].siz,tre[p.s[1]].siz);
	return merg(merg(p.s[0],y),p.s[1]);
}
int st[MAXN],tp;
void distr(int x) {
	if(!x) return ;
	distr(tre[x].s[0]);distr(tre[x].s[1]);
	tre[x].s[0] = tre[x].s[1] = 0;
	st[++ tp] = update(x);
	return ;
}
bool pb(int a,int b,LL nm) {
	return (tre[b].y - tre[a].y) < (tre[b].x - tre[a].x) *1ll* nm;
}
//------------------------------------
struct it{
	int v,w;
	it(){v=w=0;}
	it(int V,int W){v=V;w=W;}
};
vector<it> g[MAXN];
LL dp1[MAXN],d[MAXN];
int f[MAXN],ed[MAXN],rt[MAXN];
int bing(int ra,int rb) {
	if(tre[ra].siz > tre[rb].siz) swap(ra,rb);
	tp = 0;
	distr(ra);
	for(int i = 1;i <= tp;i ++) rb = ins(rb,st[i]);
	return rb;
}
void dfs(int x,int fa,int fe) {
	dp1[x] = 0; d[x] = d[f[x] = fa] + (ed[x] = fe);
	rt[x] = 0;
	for(int i = 0;i < (int)g[x].size();i ++) {
		int y = g[x][i].v,w = g[x][i].w;
		if(y != fa) {
			dfs(y,x,w);
			rt[x] = bing(rt[x],rt[y]);
//			printf("%d -> %dn",x,y);
//			print(rt[x]);
//			ENDL;
		}
	}
	int ad = tre[rt[x]].siz;
	for(int i = 20;i >= 0;i --) {
		if(ad-(1<<i) > 0 && pb(findp(rt[x],ad-(1<<i)),findp(rt[x],ad-(1<<i)+1),-1ll*(a[x] + d[x]))) {
			ad -= (1<<i);
		}
	}
	ad = findp(rt[x],ad);
	dp1[x] = max(dp1[x],(a[x] + d[x]) *1ll* tre[ad].x + tre[ad].y);
	LL Y = dp1[x] - d[x] *1ll* b[x];
	rt[x] = ins(rt[x],newnode(b[x],Y));
	return ;
}
int main() {
	freopen("journey.in","r",stdin);
	freopen("journey.out","w",stdout);
	n = read();
	for(int i = 1;i <= n;i ++) a[i] = read(),b[i] = read();
	for(int i = 1;i < n;i ++) {
		s = read();o = read();k = read();
		g[s].push_back(it(o,k));
		g[o].push_back(it(s,k));
	}
	dfs(1,0,0);
	for(int i = 1;i <= n;i ++) {
		printf("%lldn",dp1[i]);
	}
	return 0;
}