介绍

李超树用以解决一种问题：向平面上插入若干条直线（或线段），查询与直线x=a相交线段的交点坐标y的最大值，

别看这种问题好像挺个别，很多平面题或DP(斜率优化)的题都可以转换成这种问题，而遇到这种问题，李超树比平衡树好打得多。

思想

李超树代码看上去和普通线段树非常像，不同的是，每个节点维护的不是的区间，而是两端x坐标为 l、r 的一条带斜率的线段：

（注意，每层的线段高低关系不确定，这样画只是为了好看）

这样查询只需像线段树那样查就是了，

然后怎么插入线段呢？（直线就是 -inf 到 inf 的线段）只需像线段树那样插入，遇到线段与区间重合时，有如下三种情况：

1. 新线段在旧线段上方直接覆盖即可
2. 新线段在旧线段下方直接忽略即可
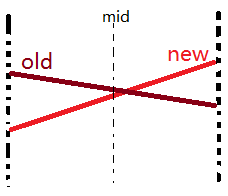3. 新旧线段相交，把其中任意一条线段分开，插入到两个儿子中，然后该节点保留另一条线段。这样做的复杂度其实等价于把这两条线段分开，必定有一边相交，另一边不相交，不相交的就是1，2两种情况，O(1)判掉，这样往下传下去就是一个log。

插入线段的复杂度最坏是（插入直线是的，因为只对应一个区间），查询是，总的复杂度就是~。

板子

代码大概长这样（直线动态开点版）：

#define INF 0x7f7f7f7f
#define ll long long
int IN;
struct lcs{
	int ls,rs;ll k,b;lcs(){}
	lcs(ll K,ll B){ls=rs=0,k=K,b=B;}
}t[MAXN<<4];
inline void add(int x,ll l,ll r,ll k,ll b){//插入一条y=kx+b的直线
	if(x==0)return;
	ll tk=t[x].k,tb=t[x].b,mid=(l+r)>>1;
	if(l*k+b>=l*tk+tb&&r*k+b>=r*tk+tb){
		t[x].k=k,t[x].b=b;return;
	}
	else if(l*k+b<l*tk+tb&&r*k+b<r*tk+tb)return;
	else{
		if(!t[x].ls)t[x].ls=++IN,t[IN]=lcs(tk,tb);
		else add(t[x].ls,l,mid,tk,tb);
		if(!t[x].rs)t[x].rs=++IN,t[IN]=lcs(tk,tb);
		else add(t[x].rs,mid+1,r,tk,tb);
		t[x].k=k,t[x].b=b;
	}
}
inline ll sch(int x,ll l,ll r,ll g){//查找x=g处的最高点
	if(x==0)return -INF;
	ll mid=(l+r)>>1,res=g*t[x].k+t[x].b;
	if(g<=mid)res=max(res,sch(t[x].ls,l,mid,g));
	else res=max(res,sch(t[x].rs,mid+1,r,g));
	return res;
}

最后

以上就是自然板栗为你收集整理的李超树——倾斜的线段树介绍思想板子的全部内容，希望文章能够帮你解决李超树——倾斜的线段树介绍思想板子所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。