CodeForces - 1000C. Covered Points Count 好题

81 阅读 0 评论 54 点赞

我是靠谱客的博主结实唇彩，最近开发中收集的这篇文章主要介绍CodeForces - 1000C. Covered Points Count 好题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

C. Covered Points Count

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given nn segments on a coordinate line; each endpoint of every segment has integer coordinates. Some segments can degenerate to points. Segments can intersect with each other, be nested in each other or even coincide.

Your task is the following: for every k∈[1..n]k∈[1..n], calculate the number of points with integer coordinates such that the number of segments that cover these points equals kk. A segment with endpoints lili and riri covers point xx if and only if li≤x≤rili≤x≤ri.

Input

The first line of the input contains one integer nn (1≤n≤2⋅1051≤n≤2⋅105) — the number of segments.

The next nn lines contain segments. The ii-th line contains a pair of integers li,rili,ri (0≤li≤ri≤10180≤li≤ri≤1018) — the endpoints of the ii-th segment.

Output

Print nn space separated integers cnt1,cnt2,…,cntncnt1,cnt2,…,cntn, where cnticnti is equal to the number of points such that the number of segments that cover these points equals to ii.

Examples

input

Copy

output

Copy

6 2 1

input

Copy

output

Copy

5 2 0

Note

The picture describing the first example:

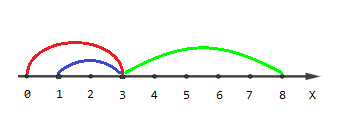
Points with coordinates [0,4,5,6,7,8][0,4,5,6,7,8] are covered by one segment, points [1,2][1,2] are covered by two segments and point [3][3] is covered by three segments.

The picture describing the second example:

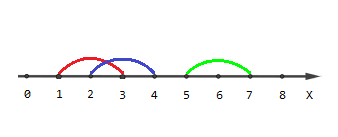
Points [1,4,5,6,7][1,4,5,6,7] are covered by one segment, points [2,3][2,3] are covered by two segments and there are no points covered by three segments.

分析：

比赛时候确实没想出这个1，-1确实妙啊。

思路：

把每个线段的起点终点分别存起来，起点标记为1，终点标记为-1，然后按照起点终点的位置排序。说不清，放个图吧。
比如
3
0 3
1 3
3 8
这组样例，排完序之后的顺序就是图中绿色的编号。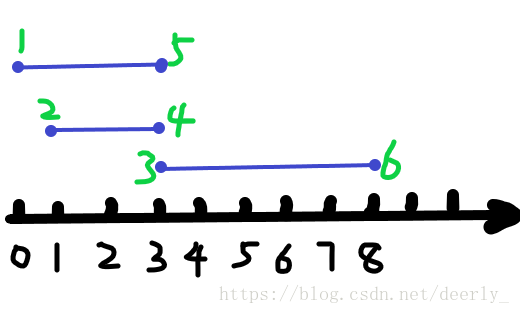
这里写图片描述
我们发现，1点的标记是1，二点的标记也是1，证明他们都是起点，一开始我们设一个计数变量，我们发现点被覆盖的次数就是计数变量原来的值加上当前点的标记，这就是为什么要给起点终点标记为1，-1了。然后到达一个起点或终点的时候，只需要后边的点的编号减去前边的点编号就是我们要的被覆盖的点的个数了。
但是有个地方就变得很难处理了，我们发现345这三个点重合了，按照原来的方式求的就不对了。怎么办呢。
只要把终点往后移一个就ok了。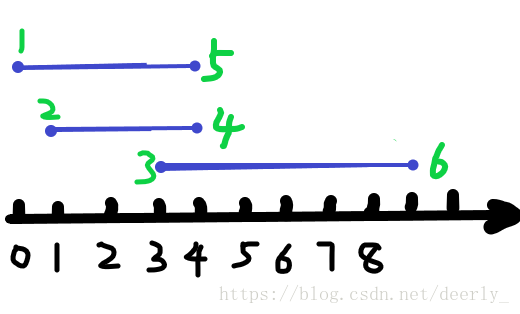
这里写图片描述

转自：https://blog.csdn.net/deerly_/article/details/80845448

代码实现：

编译错误（code block）能实现

#include <bits/stdc++.h>
#define cl(a) memset(a,0,sizeof(a))
using namespace std;
const int maxn=1e5+50;
const int inf=0x3f3f3f3f;
const int mod=1e9+7;
typedef long long ll;
typedef pair<ll,ll> E;
vector<E>a;
ll ans[maxn];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    cl(ans);
    for(int i=1;i<=n;i++)
    {
        ll x,y;
        cin>>x>>y;
        a.push_back({x,1});
        a.push_back({y+1,-1});
    }
    sort(a.begin(),a.end());
    int now=0;
    for(int i=1;i<a.size();i++)
    {
        now+=a[i-1].second;
        ans[now]+=a[i].first-a[i-1].first;

    }
    for(int i=1;i<=n;i++)
    {
        cout<<ans[i]<<" ";
    }

    return 0;
}

AC代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;

typedef long long ll;
const int maxn = 2e5 + 100;

struct node {
   ll l;
   int is;
  
};
bool cmp(node a,node b)
{
	if(a.l==b.l)
	return a.is>b.is;
	else
	return a.l<b.l;
		
}
vector<node> data;
ll ans[maxn];

int main()
{
    int n;
    scanf("%d", &n);
    ll s, e;
    for(int i = 0; i < n; i++) {
        scanf("%lld %lld", &s, &e);
        data.push_back((node) {s, 1});
        data.push_back((node) {e + 1, -1});
    }

    sort(data.begin(), data.end(),cmp);

    int len = data.size();
    int cnt = 1;
    for(int i = 1; i < len; i++) {
        ans[cnt] += data[i].l - data[i - 1].l;
        cnt += data[i].is;
    }

    for(int i = 1; i <= n; i++) {
         printf("%lld%c", ans[i], i == n ? 'n' : ' ');
    }
}