机器学习笔试题精选（五）

红色石头的个人网站：redstonewill.com

机器学习是一门理论性和实战性都比较强的技术学科。在应聘机器学习相关工作岗位时，我们常常会遇到各种各样的机器学习问题和知识点。为了帮助大家对这些知识点进行梳理和理解，以便能够更好地应对机器学习笔试包括面试。红色石头准备在公众号连载一些机器学习笔试题系列文章，希望能够对大家有所帮助！

今天的笔试题主要涉及的知识点包括：SVM、高斯核、F1 score、Leave-One_out 交叉验证、神经网络、隐马尔可夫模型等。

Q1. 假设我们在支持向量机（SVM）算法中对 Gamma（RBF 核系数 γ）的不同值进行可视化。由于某种原因，我们忘记了标记伽马值的可视化。令 g1、g2、g3 分别对应着下面的图 1、图 2 和图 3。则关于 g1、g2、g3 大小下列说法正确的是？

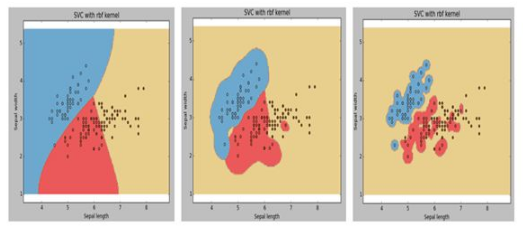
A. g1 > g2 > g3

B. g1 = g2 = g3

C. g1 < g2 < g3

D. g1 > g2 = g3

E. g1 < g2 = g3

答案：C

解析：本题考查的是 Kernel SVM 中 Gamma γ 对模型形状的影响。

SVM 中为了得到更加复杂的分类面并提高运算速度，通常会使用核函数的技巧。径向基核函数（RBF）也称为高斯核函数是最常用的核函数，其核函数的表达式如下所示：

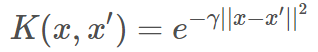
形式与高斯分布类似，Gamma γ 是高斯分布中标准差 Sigma σ 的导数。我们知道在高斯分布中，σ 越小，对应的高斯曲线就越尖瘦。也就是说 γ 越大，高斯核函数对应的曲线就越尖瘦。这样，运用核技巧得到的 SVM 分类面就更加曲折复杂，甚至会将许多样本隔离成单个的小岛。

下面是 γ 分别取 1、10、100 时对应的 SVM 分类效果：

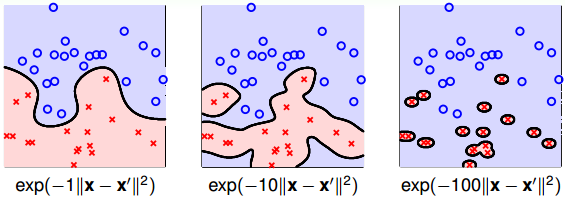
值得一提的是，γ 过小容易造成欠拟合，γ 过大容易造成过拟合。

Q2. 我们知道二元分类的输出是概率值。一般设定输出概率大于或等于 0.5，则预测为正类；若输出概率小于 0.5，则预测为负类。那么，如果将阈值 0.5 提高，例如 0.6，大于或等于 0.6 的才预测为正类。则准确率（Precision）和召回率（Recall）会发生什么变化（多选）？

A. 准确率（Precision）增加或者不变

B. 准确率（Precision）减小

C. 召回率（Recall）减小或者不变

D. 召回率（Recall）增大

答案：AC

解析：本题考察的是二元分类阈值提高对准确率和召回率的影响。

首先来看一下什么是准确率和召回率，下面分别用 P 和 R 代表。以一个简单的例子来说明，例如预测 20 个西瓜中哪些是好瓜，这 20 个西瓜中实际有 15 个好瓜，5 个坏瓜。某个模型预测的结果是：16 个好瓜，4 个坏瓜。其中，预测的 16 个好瓜中有 14 个确实是好瓜，预测的 4 个坏瓜中有 3 个确实是坏瓜。下面以一张图表说明：

这样，准确率 P 的定义是：

$$P=frac{TP}{TP+FP}$$

可以理解为预测好瓜中，确实是好瓜的比例。该例子中 P = 14/(14+2)。

召回率 R 的定义是：

$$R=frac{TP}{TP+FN}$$

可以理解为真实的好瓜被预测出来的比例。该例子中 R = 14/(14+1)。

现在，如果二元分类阈值提高，相当于判定好瓜的标准更严格了。所以可能会造成预测是好瓜的数目减少，即 TP 和 FP 均减小。因此准确率可能会增加，极端的，苛刻条件，只预测一个是好瓜，那该瓜是好瓜的概率会很大，即准确率很高。但是 15 个好瓜你只挑出来 1 个，召回率就降低了。

准确率和召回率都不能很好地反映模型性能，通常使用 F1 score 来作为模型预测水平判据。F1 Score 被定义为准确率和召回率的调和平均数。，如下所示：

$$F1=2cdotfrac{Pcdot R}{P+R}$$

Q3. 点击率预测是一个正负样本不平衡问题（例如 99% 的没有点击，只有 1% 点击）。假如在这个非平衡的数据集上建立一个模型，得到训练样本的正确率是 99%，则下列说法正确的是？

A. 模型正确率很高，不需要优化模型了

B. 模型正确率并不高，应该建立更好的模型

C. 无法对模型做出好坏评价

D. 以上说法都不对

答案：B

解析：这一题延续了上题中准确率和召回率的知识点，考查了正负样本分布不均问题。

模型训练过程中正负样本分布不均是常见的问题。这时候不能单独只看预测正确率。对于此题来说，如果我们预测的结果是 100% 没有点击，0% 点击，那么可以说正确率是 99%，因为只有 1% 的点击预测错误。但是，我们其实更关心的那 1% 的点击率并没有预测出来。可以说这样的模型是没有任何意义的。

对应正负样本不平衡的情况需要做一些数据处理，主要包括：采样、数据合成、惩罚因子加权、一分类。其中，一分类即是在正负样本分布极不平衡的时候，把它看做一分类（One Class Learning）或异常检测（Novelty Detection）问题。这类方法的重点不在于捕捉类间的差别，而是为其中一类进行建模，经典的工作包括 One-class SVM 等。

Q4. 假设我们使用 kNN 训练模型，其中训练数据具有较少的观测数据（下图是两个属性 x、y 和两个标记为 “+” 和 “o” 的训练数据）。现在令 k = 1，则图中的 Leave-One-Out 交叉验证错误率是多少？

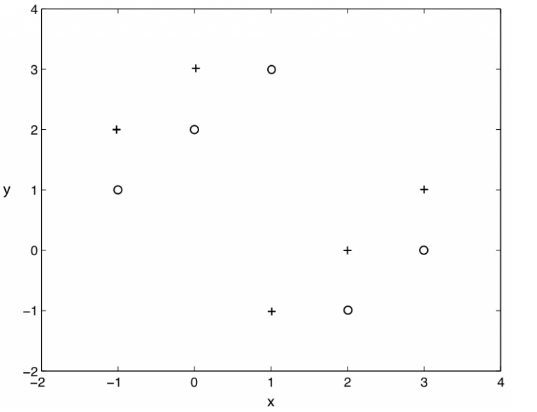
A. 0%

B. 20%

C. 50%

D. 100%

答案：D

解析：本题考查的是 kNN 算法和 Leave-One-Out 交叉验证。

kNN 算法是标记类算法，取当前实例最近邻的 k 个样本，k 个样本中所属的最多类别即判定为该实例的类别。本题中 k = 1，则只需要看最近邻的那一个样本属于“+” 还是“o”即可。

Leave-One-Out 交叉验证是一种用来训练和测试分类器的方法，假定数据集有N 个样本，将这个样本分为两份，第一份 N-1 个样本用来训练分类器，另一份 1 个样本用来测试，如此迭代 N 次，所有的样本里所有对象都经历了测试和训练。

分别对这 10 个点进行观察可以发现，每个实例点最近邻的都不是当前实例所属的类别，因此每次验证都是错误的。整体的错误率即为 100%。

Q5. 如果在大型数据集上训练决策树。为了花费更少的时间来训练这个模型，下列哪种做法是正确的？

A. 增加树的深度

B. 增加学习率

C. 减小树的深度

D. 减少树的数量

答案：C

解析：本题考查的是决策树相关概念。

一般用决策树进行分类，从根结点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到其子结点。这时，每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分类，直至达到叶结点。最后将实例分到叶结点的类中。—— 引自李航 《统计学习方法》

决策树深度越深，在训练集上误差会越小，准确率越高。但是容易造成过拟合，而且增加模型的训练时间。对决策树进行修剪，减小树的深度，能够提高模型的训练速度，有效避免过拟合。

单决策树中，学习率不是一个有效参数。

决策树是单树，随机森林由多个决策树组成。

Q6. 关于神经网络，下列说法正确的是？

A. 增加网络层数，可能会增加测试集分类错误率

B. 增加网络层数，一定会增加训练集分类错误率

C. 减少网络层数，可能会减少测试集分类错误率

D. 减少网络层数，一定会减少训练集分类错误率

答案：AC

解析：本题考查的是神经网络层数对训练误差和测试误差的影响。

一般来说，神经网络层数越多，模型越复杂，对数据的分类效果越好。所以，从最简单的层数开始，增加网络层数都能使得训练误差和测试误差减小。但是，神经网络层数过多容易造成过拟合，即对训练样本分类效果很好，误差小，但是测试误差很大。

为了避免发生过拟合，应该选择合适的神经网络层数并使用正则化技术来让神经网络更加稳健。

Q7. 假设我们使用原始的非线性可分版本的 Soft-SVM 优化目标函数。我们需要做什么来保证得到的模型是线性可分离的？

A. C = 0

B. C = 1

C. C 正无穷大

D. C 负无穷大

答案：C

解析：本题考查的是 SVM 和 Soft-SVM 之间的联系和彼此转化条件。

Soft-SVM 在原来的 SVM 基础上增加了分类错误项，如下式：

$$min(b,w,xi) frac12w^Tw+Ccdot sum_{n=1}^Nxi_n$$

其中，第二项即为分类错误项。C 为参数类似于正则化中的惩罚因子。其中， ξn 表示每个点犯错误的程度，ξn = 0，表示没有错误，ξn 越大，表示错误越大，即点距离边界（负的）越大。参数 C 表示尽可能选择宽边界和尽可能不要犯错两者之间的权衡，因为边界宽了，往往犯错误的点会增加。large C 表示希望得到更少的分类错误，即不惜选择窄边界也要尽可能把更多点正确分类；small C 表示希望得到更宽的边界，即不惜增加错误点个数也要选择更宽的分类边界。因此，C 正无穷大时，可以实现没有分类错误的点，模型线性可分。

从另一方面来看，线性可分 SVM 中，对偶形式解得拉格朗日因子 αn≥0；而在 Soft-SVM 中，对偶形式解得拉格朗日因子 0 ≤ αn ≤ C。显然，当 C 无正无穷大的时候，两者形式相同。

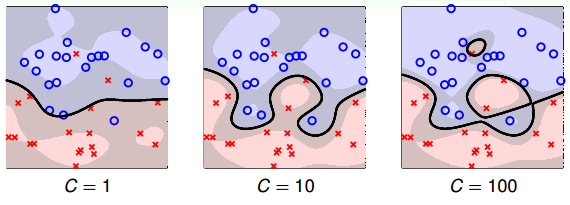
值得一提的是，当 C 值很大的时候，虽然分类正确率提高，但很可能把 noise 也进行了处理，从而可能造成过拟合。也就是说 Soft-SVM 同样可能会出现过拟合现象，所以参数 C 的选择非常重要。下图是 C 分别取1、10、100时，相应的分类曲线：

Q8. 在训练完 SVM 之后，我们可以只保留支持向量，而舍去所有非支持向量。仍然不会影响模型分类能力。这句话是否正确？

A. 正确

B. 错误

答案：A

解析：本题考查的是对支持向量机 SVM 的概念理解。

其实，刚学习支持向量机时会有个疑问，就是为什么会叫这个名字。该算法决定分类面的一般是关键的几个点，这几个点构建了分类面，因此被称为支持向量。该算法也就叫支持向量机了。训练完毕之后，其它非支持向量对分类面并无影响，去掉无妨。

对于线性可分的 SVM，可以根据拉格朗日因子 αn 数值来判断当前样本 (xn, yn) 是否为 SV。

• 若 αn = 0：不是 SV

• 若 αn > 0：是 SV，且分类正确

对于 Soft-SVM（线性不可分），可以根据拉格朗日因子 αn 数值与参数 C 的关系来判断当前样本 (xn, yn) 是否为 SV。

• 若 αn = 0：不是 SV，且分类正确

• 若 0 < αn < C：是 SV

• 若 αn = C：不是 SV，且分类错误（或恰好位于分类面上）

对 SVM 概念不太清楚的同学可以看看林轩田机器学习技法 1-6 对 SVM 的讲解，通俗易懂，内容翔实。对应的笔记可以在本公众号查阅，放上第 1 讲链接：

深入浅出机器学习技法（一）：线性支持向量机

Q9. 下列哪些算法可以用来够造神经网络（多选）？

A. kNN

B. 线性回归

C. 逻辑回归

答案：BC

解析：本题考查的是 kNN、线性回归、逻辑回归与神经网络之间的一些关系。

kNN 是一种基于实例的学习算法，不具有任何训练参数。因此不能用来构造神经网络。

线性回归和逻辑回归都可以用来构造神经网络模型，其实二者就是单神经元的神经网络。

Q10. 下列数据集适用于隐马尔可夫模型的是？

A. 基因数据

B. 影评数据

C. 股票市场价格

D. 以上所有

答案：D

解析：本题考查的是隐马尔可夫模型适用于解决哪类问题。

隐马尔可夫模型（Hidden Markov Model，HMM）是关于时序的概率模型，描述一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观察而产生观测随机序列的过程。因此，隐马尔可夫模型适用于解决时间序列问题。

参考文献：

Solutions for Skilltest Machine Learning : Revealed

---

最后

以上就是听话盼望为你收集整理的机器学习笔试题精选（五）的全部内容，希望文章能够帮你解决机器学习笔试题精选（五）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。