一. 线性结构的基本特点
除第一个元素无直接前驱,最后一个元素无直接后继外,其他每个数据元素都有一个前驱和后继。
二. 线性表的特点和定义
1.由n(n>=0)个数据特性相同的元素构成的有限序列称为线性表。
2.线性表中的个数n定义为线性表的长度,n=0时称为空表
3.对于非空线性表和线性结构的特点
存在唯一的一个被称作“第一个”的数据元素
存在唯一的一个被称作“最后一个”的数据元素
除第一个之外,结构中的每个数据元素均只有一个前驱
除最后一个之外,结构中的每个数据元素均只有一个后继
三. 线性表的顺序存储表示
1.用一组地址连续的存储单元依次存储线性表的数据元素,称这种存储结构的线性表为顺序表。
特点是逻辑上相邻的数据元素,其物理次序也是相邻的。
2.假设线性表的每个元素需占用l个存储单元
LOC(a i+1)=LOC(a i)+ l
LOC(a i)=LOC(a 1)+(i-1)* l
3.线性表中的任意数据元素都可随机存取,所以线性表的顺序存储结构是一种随机存取的存储结构。
4.表示
常用数组来描述数据结构中的顺序存储结构
#define MAXSIZE 100//顺序表可能达到的最大长度
typedef struct
{
type *elem;//存储空间的地址
(或者type data[MAXSIZE])
int length;//长度
}Sqlist四.线性表的顺序存储的基本操作
1.初始化
构造一个空的顺序表
Status Initlist(Sqlist &L)
{
L.elem=new elemtype[MAXSIZE];//为顺序表分配一个大小为MAXSIZE的数组空间
if(!L.elem)
exit(OVERFLOW);//存储分配失败退出
L.length=0;//空表长度置为0
return ok;
}也可利用动态存储有效利用系统资源
2.取值
获取顺序表中第i个元素的值,算法时间复杂度为O(1)
Status Getelem(Sqlist L,int i,Elemtype &e)
{
if(i<1||i>L.length)
return ERROR;
e=L.elem[i-1];
return ok;
}3.查找
查找数值为e的元素返回其序号,平均时间复杂度为O(n)
int Locateelem(Sqlist L,elemtype e)
{
for(i=0;i<L.length;i++)//遍历数组
{
if(L.elem[i]==e)
return i+1;//找到后返回序号
}
return 0;//查找失败返回0
4.插入
在表的第i个位置插入一个新的数据元素e
将ai之后的数据(倒序)往后移一位,然后插入,表长加一
时间复杂度为O(n)
Status Listinsert(Sqlist &L,int i,Elemtype e)
{
if(i<1||i>L.length+1)//判断i是否合法
return ERROR;
if(i>MAXSIZE)
return ERROR;
for(j=L.length-1;j>=i-1;j--)//倒序
{
L.elem[j+1]=L.elem[j];//将元素后移
}
L.elem[i-1]=e;//插入新值
++L.length;//表长加一
return ok;
}5.删除
删去第i个元素,即将ai之后的元素依次前移
平均时间复杂度为O(n)
Status Listdelete(Sqlist &L,int i)
{
if(i<1||i>L.length+1)
return ERROR;//不合法输入
for(j=i;j<L.length;j++)//正序
{
L.elem[j-1]=L.elem[j];//前移
}
L.length--;//表长减1
return ok;
}五. 线性表的链式表示
1.用一组任意的存储单元存储线性表的数据元素
!这组存储单元(物理位置)既可以是连续的也可以是不连续的
2.结点
信息+后继的存储位置
数据域+指针域
n个结点链接成一个链表
3.表示
typedef struct LNode
{
elemtype data;//数据元素
struct LNode *next;//后继指针
}NOde,*Linklist;
4.首元结点,头结点,头指针
首元结点是指链表中存储第一个元素a1的结点
头结点是在首元结点之前设的一个结点,其指针域指向首元结点,数据域可以不存储信息也可以存储长度
头指针是指向链表中第一个结点的指针(指向头结点或首元结点)
链表增加头结点的作用
*便于首元结点的处理,不需进行特殊处理
*便于空表和非空表的统一处理,头指针都是指向头结点的非空指针
单链表是顺序存取的存取结构
六.单链表基本操作
1.初始化
生成新结点,头指针指向头结点,头指针的指针域置空
Status Initlist(Linklist &L)
{
L=new Lnode;
L.next=NULL;
return ok;
}
2.取值
从首元结点开始依次访问,取第i个值
(n-1)/2 平均时间复杂度为O(n)
Status Get(Linklist &L,int i,Elemtype &e)
{
p=L->next;//指向首元结点
j=1;//计数
while(p&&j<i)//必须判断p非空
{
p=p->next;
j++;
}
if(!p||j>i)//!p对应i>n,j>i对应输入i<0
return error;
e=p->data;//找到目标数据
return ok;
}
3.按值查找
遍历,平均时间复杂度O(n)
Lnode *LocateElem(Linklist L,Elemtype e)
{
p=L->next;
while(p)
{
if(p->data!=e)
p=p->next;
else return p;
}
}
4.插入
将值为e的新结点插入第i个结点的位置,先找到该位置的前驱
平均时间复杂度O(n)
Status Listinsert(Linklist &L,int i,Elemtype e)
{
p=L;
j=0;//如果是p=l->next,j=1需特殊处理i=1的情况
while(p&&j<i-1)
{
j++;
p=p->next;
}//找到要插入的位置,此时p指向a(i-1)
if(!p||(j>i-1))
return error;
s=new LNode;//创建新结点
s->data=e;//为新结点赋值
s->next=p->next;//将ai和新结点连接起来
p->next=s;//将新结点链到a(i-1)后
}5.删除
修改待删除结点前驱的指针域以及释放待删除结点所占空间
平均时间复杂度是O(n)
Status ListDelete(LinkList &l,int i)
{
p=L;
j=0;
while((p->next)&&(j<i-1))//找待删除结点的前驱,所以是p->next
{
p=p->next;
j++;
}
if((p->next==NULL)||(j>i-1))
return error;
q=p->next;//临时保存待删结点以备释放
p->next=q->next;//待删结点前驱与后继链接
delete q;//释放删除结点
return ok;
}
注意:
删除操作中的循环条件和插入不一样,
删除while((p->next)&&(j<i-1))
插入while(p&&j<i-1)
插入操作可以出现被插入位置前驱是最后一个结点的情况,即插入到最后一个结点之后,i=n+1,而删除操作不会出现待删除结点前驱是最后一个结点的情况,因为没有这个结点。
6.创建单链表
A后插法创建单链表
将新结点插入链表的尾部,按输入顺序构建链表存储数据
时间复杂度O(n)
void Createlist_R(LinkList &L,int n)
{
L=new LNode;//建立一个空链表
L->next=NULL;
r=L;//设置一个尾指针
for(i=0;i<n;i++)
{
p=new LNode;//建立一个新结点
cin>>p->data;//输入数据
p->next=NULL;//尾
r->next=p;//将p连到尾指针之后
r=p;//r指向新的尾结点
}
}
B头插法创建单链表
将每一个新结点插入链表的头部,头结点之后
时间复杂度为O(n)
void CreatList_H(LinkList &L,int i)
{
L=new LNode;
L-next=NULL;//先建立一个带头指针的空链表
for(i=0;i<n;i++)
{
p=new LNode;//新结点
cin>>p->data;//输入数据
p-next=L->next;//将第i+1个结点即新结点的指针域指向第i个结点
L->next=p;//新结点插入头结点之后
}
}七.循环链表和双向链表
1.循环链表
链表中最后一个结点的指针域指向头结点,整个链表形成一个环
与单链表的差别:终止条件不同
单链表p!=NULL或p->next!=NULL
循环链表p!=L或p->next!=NULL
利用循环链表合并两个链表
A,B是两个链表的尾结点
p=B->next->next;//p指向头结点之后的即首元结点
B->next=A->next;//将B的尾结点指针域指向A的首结点
A->next=p;//将B的首元结点连到A的尾结点之后
2.双向链表
双向链表的结点中有两个指针域,一个指向直接后继,一个指向直接前驱
定义
typedef struct DuLNode
{
ElemType data;
struct DuLNode *prior;
struct DuLNode *next;
}DuLNode,*DuLinklist;双向链表的插入
Status ListInsert(DuLinkList &L,int i,ElemType e)
{
if(!(p=GetElem(L,i)))//确定第i个元素的位置指针
return error;
s=new DuLNode;//创建新结点
s->data=e;
s->piror=p->piror;//将s的前驱指向p的前驱
p->piror->next=s;//将p的前驱的后继指向s
s->next=p;//将s的后继指向p
p->piror=s;//将p的前驱指向s
return ok;
}
双向链表的删除
Status Listdelete(DuLinkList &L,int i)
{
if(!(p=(GetElem_DuL(L,i)))
return error;
p->piror->next=p->next;
p->next->piror=p->piror;
delete p;
return ok;
}
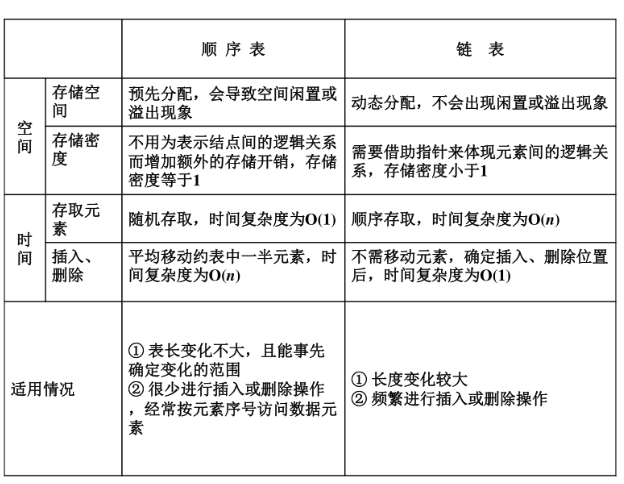
八.顺序表和链表的比较
1.顺序表的存储空间必须预先分配,受到限制,易造成空间浪费或空间不够
当线性表的长度变化较大,难以估计,宜采用链表作为存储结构
2.存储密度=数据元素本身占用的存储量/结点结构占用的存储量
存储密度越大,存储空间的利用率越高
顺序表的存储密度是1,单链表存储密度为0.5
当线性表的长度变化不大,易于事先确定时,为了节约存储空间,宜采用顺序表
3.数组是一种随机存取结构,而链表是一种顺序存取结构
当线性表的主要操作是与位置有关的,插入和删除操作较少,宜采用顺序表
最后
以上就是可耐眼神最近收集整理的关于线性表的全部内容,更多相关线性表内容请搜索靠谱客的其他文章。








发表评论 取消回复