1、题目

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

进阶：

• 你可以设计并实现时间复杂度为 O(log n) 的算法解决此问题吗？

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

提示：

• 0 <= nums.length <= 105
• -109 <= nums[i] <= 109
• num 是一个非递减数组
• -109 <= target <= 109

2、思路

(二分) O(logn)O(logn)O(logn)

在一个范围内，查找一个数字，要求找到这个元素的开始位置和结束位置，这个范围内的数字都是单调递增的，即具有单调性质，因此可以使用二分来做。

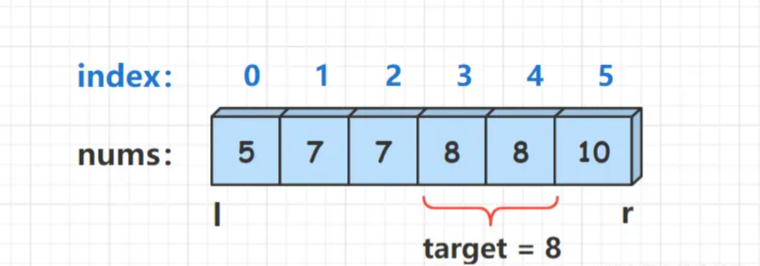
两次二分，第一次二分查找第一个>=target的位置，第二次二分查找最后一个<=target的位置。查找成功则返回两个位置下标，否则返回[-1,-1]。

实现细节：

• 二分查找时，首先要确定我们要查找的边界值，保证每次二分缩小区间时，边界值始终包含在内。

第一次查找起始位置:

• 1、二分的范围，l = 0， r = nums.size() - 1，我们去二分查找>=target的最左边界。
• 2、当nums[mid] >= target时，往左半区域找，r = mid。
• 3、当nums[mid] < target时， 往右半区域找，l = mid + 1。

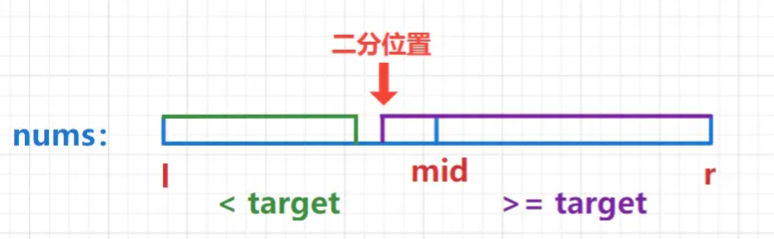
• 4、如果 nums[r] != target，说明数组中不存在目标值 target，返回 [-1, -1]。否则我们就找到了第一个>=target的位置L。

第二次查找结束位置：

• 1、二分的范围，l = 0， r = nums.size() - 1，我们去二分查找<=target的最右边界。
• 2、当nums[mid] <= target时，往右半区域找，l = mid。
• 3、当nums[mid] > target时， 往左半区域找，r = mid - 1。
• 4、找到了最后一个<=target的位置R，返回区间[L,R]即可。

时间复杂度分析： 两次二分查找的时间复杂度为 O(logn)O(logn)O(logn)。

3、c++代码

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        if(nums.empty()) return {-1,-1};
    
        int l = 0, r = nums.size() - 1; //二分范围
        while( l < r)			//查找元素的开始位置
        {
            int mid = (l + r )/2;
            if(nums[mid] >= target) r = mid;
            else l = mid + 1;
        }
        if( nums[r] != target) return {-1,-1};
        int L = r;
        l = 0, r = nums.size() - 1;
        while( l < r)          //查找元素的结束位置
        {
            int mid = (l + r + 1)/2;
            if(nums[mid] <= target ) l = mid;
            else r = mid - 1;
        }
        return {L,r};
    }
};

4、java代码

class Solution {
    public int[] searchRange(int[] nums, int target) {
        if(nums.length == 0) return new int[]{-1,-1};
    
        int l = 0, r = nums.length - 1; //二分范围
        while( l < r)			//查找元素的开始位置
        {
            int mid = (l + r )/2;
            if(nums[mid] >= target) r = mid;
            else l = mid + 1;
        }
        if( nums[r] != target) return new int[]{-1,-1};
        int L = r;
        l = 0; r = nums.length - 1;
        while( l < r)			//查找元素的结束位置
        {
            int mid = (l + r + 1)/2;
            if(nums[mid] <= target ) l = mid;
            else r = mid - 1;
        }
        return new int[]{L,r};
    }
}

原题链接： 34. 在排序数组中查找元素的第一个和最后一个位置

最后

以上就是知性樱桃为你收集整理的字节最新算法题解：在排序数组中查找元素的第一个和最后一个位置1、题目2、思路3、c++代码4、java代码的全部内容，希望文章能够帮你解决字节最新算法题解：在排序数组中查找元素的第一个和最后一个位置1、题目2、思路3、c++代码4、java代码所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。