找两个字符串的最长公共子串,这个子串要求在原字符串中是连续的。而最长公共子序列则并不要求连续。
解题思路:
设一个C[i,j]: 保存Ai与Bj的LCS的长度。
1.首先利用一个二维数组C[i-1][j-1]来记录A串中前i-1个数和B串中的前j-1个数的最大公共子序列长度。
2.然后当我们开始挑选A,B串的下一个时即确定C[i][j]时,如果这两个相等,即A[i-1] == B[j-1],那么就可以直接把这相等的字母加进去,即C[i][j] = C[i-1][j-1] + 1.
3.当我们开始挑选A,B串的下一个时即确定C[i][j]时,如果这两个不相等,即A[i-1] != B[j-1],那么最大公共子列长度是C[i-1][j]和C[i][j-1]这两者较大值
递推方程为:
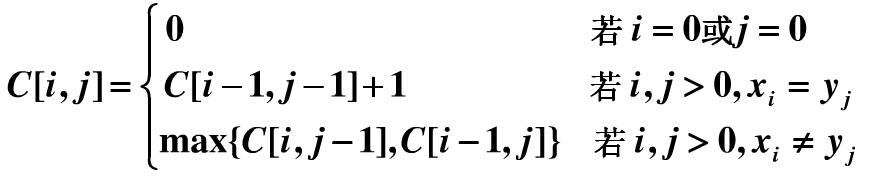
class LCS {
public:
int findLCS(string A, int n, string B, int m) {
if(n == 0 || m == 0)
return 0;
vector<vector<int>> C(n+1,vector<int>(m+1));
for(int i = 1; i <= n ; i++)
{
for( int j = 1; j <= m; j++)
if(A[i-1] == B[j-1])
C[i][j] = C[i-1][j-1] + 1;
else
C[i][j] = (C[i-1][j] >= C[i][j-1] ? C[i-1][j] : C[i][j-1]);
}
return C[n][m];
}
};
public:
int findLCS(string A, int n, string B, int m) {
if(n == 0 || m == 0)
return 0;
vector<vector<int>> C(n+1,vector<int>(m+1));
for(int i = 1; i <= n ; i++)
{
for( int j = 1; j <= m; j++)
if(A[i-1] == B[j-1])
C[i][j] = C[i-1][j-1] + 1;
else
C[i][j] = (C[i-1][j] >= C[i][j-1] ? C[i-1][j] : C[i][j-1]);
}
return C[n][m];
}
};
最后
以上就是兴奋帆布鞋最近收集整理的关于求最长公共子序列的长度的全部内容,更多相关求最长公共子序列内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。
![[leetcode]找两个有序数组的中位数](https://www.shuijiaxian.com/files_image/reation/bcimg9.png)







发表评论 取消回复