求公共最长子序列

动态规划
重叠子问题

• 两个指针进行遍历,如果两个指针指向的字符相同,说明该字符一定在子序列里,那么以该字符结尾的序列长度为
• 如果两个指针指向的字符不同,说明两指针所在位置不是子序列,固向前查找第一个指针位置减一,第二个指针位置不变和第一个位置指针不变,第二个指针位置-1的结尾的两个字串

备忘录

• 因为需要两个指针记录当前子串的位置,所以是dp[i][j]形式的二维数组

状态转移方程

if(input1[i] == input2[j]){
	T[i][j] = T[i-1][j-1] + 1;
}else{
	T[i][j] = max(T[i-1][j],T[i][j-1])
}

边界:

• 当i为0的时候text1的子串为空字符串，所以无论j为多少最长公共子序列的长度都为0，j为0的情况也是一样，所以我们可以初始化一个初始值全部为0的dp数组或当i=0或j=0时都为0的二维数组

求长度

let longestCommonSubsequence = function (text1, text2) {
    let m = text1.length
    let n = text2.length
    let max=0;
    // 初始化二维数组
    let dp = new Array(m + 1).fill(0)
    dp.forEach((item, index) => {
        dp[index] = new Array(n + 1).fill(0)
    })
    for(let i = 1; i <= m; i++) {
        // 因为i和j都是从1开始的，所以要减1
        let t1 = text1[i - 1]
        for(let j = 1; j <= n; j++) {
            let t2 = text2[j - 1]
            // 情况1
            if (t1 === t2) {
                dp[i][j] = 1 + dp[i - 1][j - 1]
                dp[i][j]>max?max=dp[i][j]:''
            } else {// 情况2
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1])
                dp[i][j]>max?max=dp[i][j]:''
            }
        }
    }
}

求最长子序列内容:
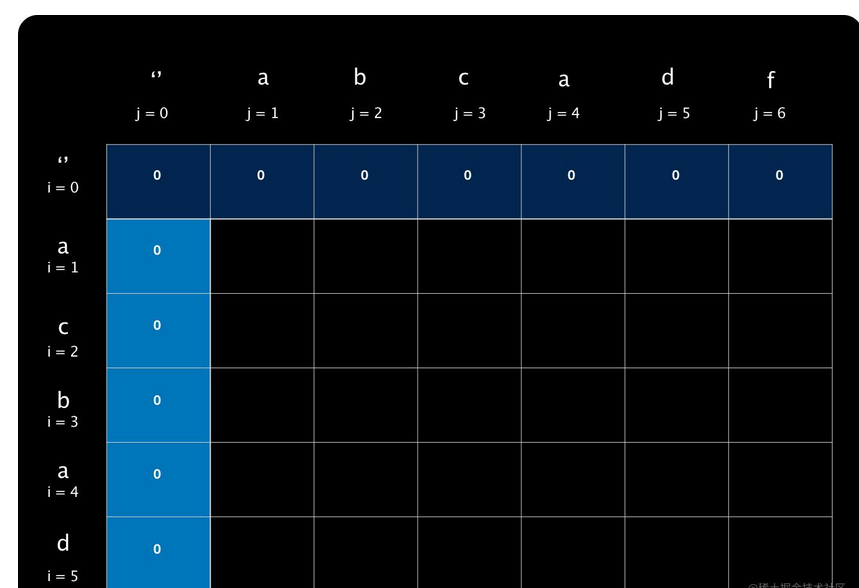i=1 j=1：此时等同于求字符串 a和a的最长公共子序列长度，很显然结果为1。
i=1 j=2：此时等同于求字符串 a和ab的最长公共子序列长度，结果为1。
i=1 j=3：此时等同于求字符串 a和abc的最长公共子序列长度，结果为1。
只要一个序列只有一个字符，那么另一个序列无论多长，它们的最长公共子序列长度最多只能为1。所以 i=1 行剩余空格都填1。
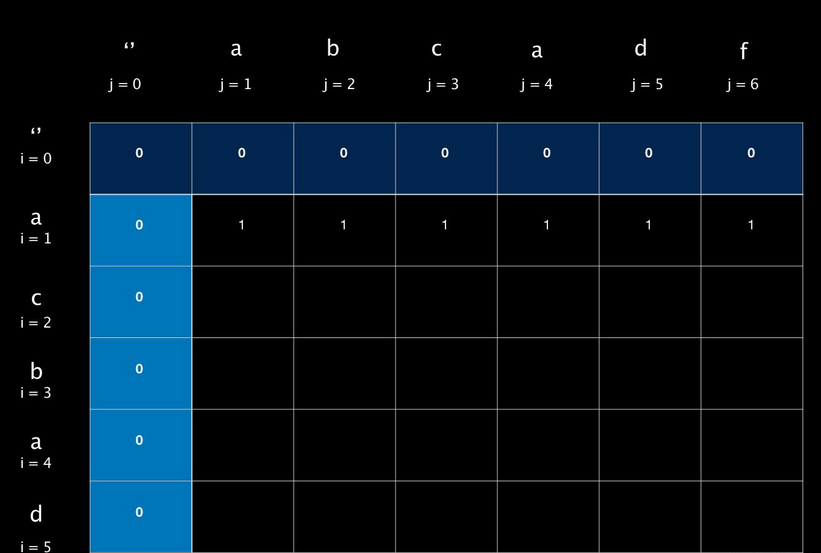最终表格
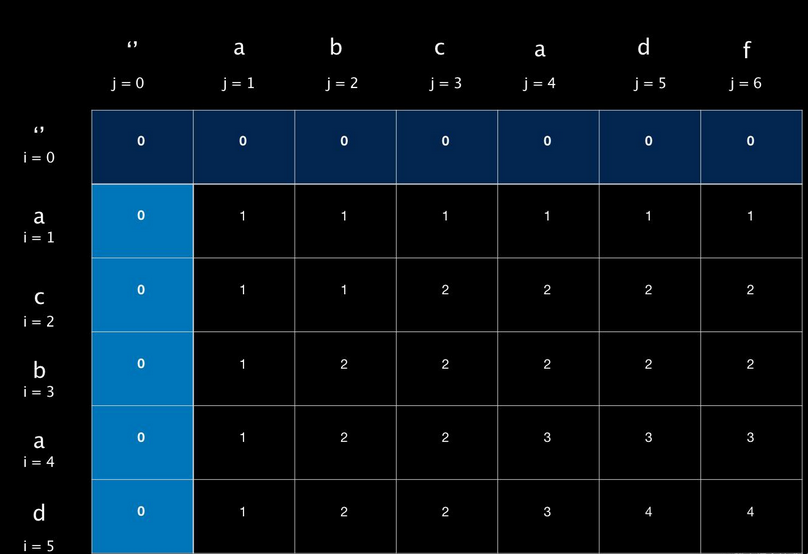比如 i=5 j=4，此时input1[i] !=input2[j]，我们取它左边（2）或者上方（3）的较大值，所以填写3。
i=5 j=5，此时input1[i] ==input2[j]，我们直接取左上角值加1，左上角的值为T[4][4]=3，所以T[5][5]=4 。
回退路径:
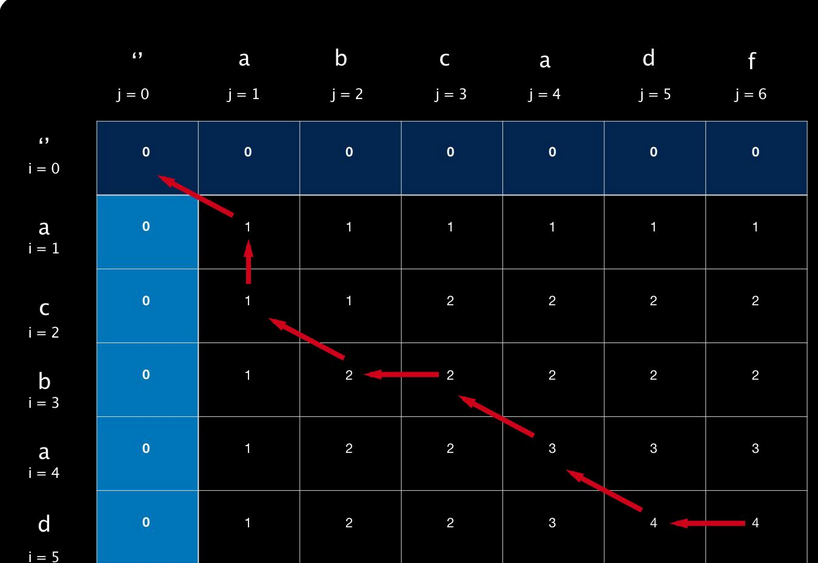最终字串为:

s = ['a','b','a','d']

寻找子串
由上方得出的规律知，回退路径为，如果input1[i] ==input2[j]，则i-1,j-1,
如果input1[i] !=input2[j]，dp[i-1][j]>dp[i][j-1]则i–,否则（包含相等,因为填表也是相等优先取左）j–向左回退，

//n1、n2为两个字串长度
//T为求公共最长长度时的dp
function findValue(input1,input2,n1,n2,T){
	var i = n1-1,j=n2-1;
	var result = [];//结果保存在数组中
	console.log(i);
	console.log(j);
	while(i>0 && j>0){
		if(input1[i] == input2[j]){
			result.unshift(input1[i]);
			i--;
			j--;
		}else{
			//向左或向上回退
			if(T[i-1][j]>T[i][j-1]){
				//向上回退
				i--;
			}else{
				//向左回退
				j--;
			}
		}

	}

	console.log(result);
}

最后

以上就是简单诺言最近收集整理的关于求公共最长子序列的全部内容，更多相关求公共最长子序列内容请搜索靠谱客的其他文章。