求最长公共子序列长度和输出

90 阅读 0 评论 60 点赞

我是靠谱客的博主忧郁电话，这篇文章主要介绍求最长公共子序列长度和输出，现在分享给大家，希望可以做个参考。

最长公共子序列

子序列概念： 一个给定序列的子序列是在该序列中删去若干元素后得到的序列。例如X=（A,B,C,B,D,A,B），X的子序列有（A,B,C,B,A)，（A,B,D)，(B,C,D,B)。子序列与子串的不同在于子串的元素在原序列中是连续的。
最长公共子序列问题： 给定两个序列X和Y，找出X和Y的一个最长公共子序列。

解决方法

最长公共子序列采用动态规划解决。动态规划关键在于找出状态和状态转移方程。
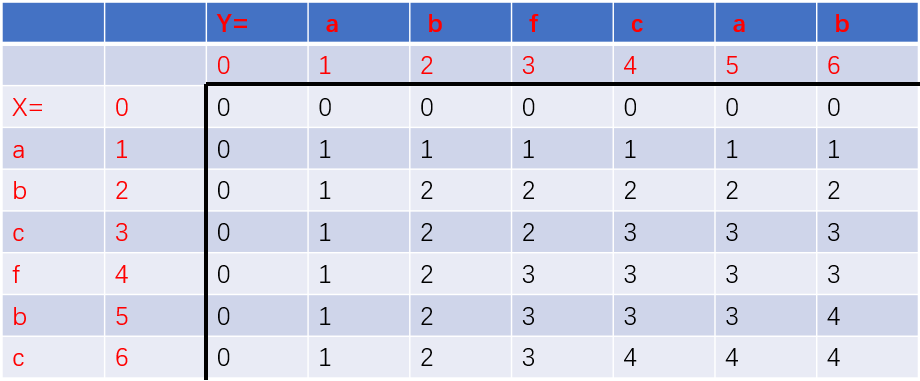
例如，序列X=（a,b,c,f,b,c)、Y=(a,b,f,c,a,b)。
状态：用L[i][j]表示子序列X_i和Y_j的最长公共子序列长度。
状态转移：

当X_i=Y_j，找出X_i-1和Y_j-1的最长公共子序列，然后在其尾部加上X_i即可得到X和Y的最长公共子序列。
当X_i != Y_j，求解两个子问题。1、求X_i-1和Y_j的最长公共子序列；2、求X_i和Y_j-1的最长公共子序列。然后取其最大值。
状态转移方程：

复制代码

1
2
3
4
 				L[i-1][j-1]+1	(当Xi=Yj,i>0,j>0)
 L[i][j]  = {
 				max(L[i][j-1],L[i-1][j])	(当当Xi!=Yj,i>0,j>0)

填表

根据上面的分析，可以知道，推导一个新的L[i][j]的值时，只需要看这个元素的左上角，左边，右边就可以。如果X_i=Y_j，则用左上角元素加1；如果X_i != Y_j，则取左边元素和上边元素的较大值。表中第一行和第一列全为0的原因：当X为空串时，不论Y是什么，它们的最长公共子序列长度都为0；反之，当Y为空串时，不论X是什么，它们的最长公共子序列长度都为0。
在这里插入图片描述

例题

例题hdu-1159

题意就是给定两个序列，然后求这两个序列的最长公共子序列的长度。

代码1

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1005;
int dp[maxn][maxn];
string str1,str2;
int LCS()
{
	memset(dp,0,sizeof(dp));
	for(int i=1;i<=str1.length();i++){
		for(int j=1;j<=str2.length();j++){
			if(str1[i-1]==str2[j-1]){
				dp[i][j]=dp[i-1][j-1]+1;
			}else{
				dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
			}
		}
	}
	/*输出最长公共子序列 
	int x=str1.length(),y=str2.length();
	string lcs;
	cout<<"----------"<<endl;
	while(x>0&&y>0){
		if(str1[x-1]==str2[y-1]){
			lcs+=str1[x-1];
			x=x-1;y=y-1;
		}else{
			if(dp[x-1][y]>dp[x][y-1]){
				x=x-1;
			}else{
				y=y-1;
			}
		}
	}
	reverse(lcs.begin(),lcs.end());
	cout<<lcs<<endl;*/
	return dp[str1.length()][str2.length()];
}
int main()
{
	while(cin>>str1>>str2){
		cout<<LCS()<<endl;
		//cout<<"----------"<<endl;
	}
		
	return 0;
}

代码2（利用滚动数组进行空间优化）

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1005;
int dp[2][maxn];
string str1,str2;
int LCS()
{
	memset(dp,0,sizeof(dp));
	int now=0; 
	for(int i=1;i<=str1.length();i++){
		for(int j=1;j<=str2.length();j++){
			if(str1[i-1]==str2[j-1]){
				dp[now^1][j]=dp[now][j-1]+1;
			}else{
				dp[now^1][j]=max(dp[now][j],dp[now^1][j-1]);
			}
			
		}
		now^=1;	
	}
	
	return dp[now][str2.length()];
}
int main()
{
	while(cin>>str1>>str2){
		cout<<LCS()<<endl;
	}
		
	return 0;
}