【剑指offer】面试题29：顺时针打印矩阵

93 阅读 0 评论 62 点赞

我是靠谱客的博主坚强店员，最近开发中收集的这篇文章主要介绍【剑指offer】面试题29：顺时针打印矩阵，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目：输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

牛客网链接：https://www.nowcoder.com/questionTerminal/9b4c81a02cd34f76be2659fa0d54342a

下面先通过一个案例讲解下什么是从外向里以顺时针的顺序依次打印出每一个数字。

当遇到一个复杂的问题的时候，我们可以用图形来帮助我们来思考。由于是从外圈到内圈的顺序依次打印，我们可以把矩阵想象成若干个圈，如图所示。我们可疑用一个循环来打印矩阵，每一次打印矩阵中的一个圈。

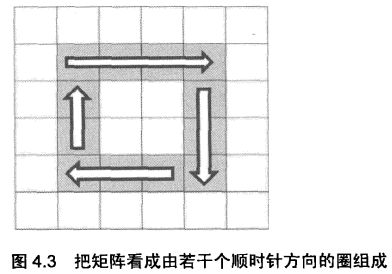
接下来分析循环结束的条件。假设这个矩阵的行数是rows，列数是columns。打印第一个圈是左上角元素的坐标是（0，0），第二圈的左上角的坐标是（1，1），依次类推。我们注意到，左上角的坐标中行标和列标总是相同的，于是可以在矩阵中选取左上角为（start，start）的一圈为我们分析的目标。

对一个5*5的矩阵而言，最后一圈只有一个数字，对应的坐标为（2，2）。我们发现5>2*2。对于一个6*6的矩阵而言，最后一圈有4个数字，其左上角的坐标仍然为（2，2）。我们发现6>2*2依然成立。于是我们可以得出继续循环的条件是columns > startX*2并且rows > startY*2。

接着我们考虑如何打印一圈的功能，即如何实现PrintMatrixInCircle。如图所示，我们可以把打印一圈分为四步：第一步从左到右打印一行，第二步从上到下打印一行，第三步从右到左打印一行，第四步从下到上打印一列。每一步我们根据起始坐标用一个循环就能打印出一行或者一列。

不过值得注意的是，最后一圈有可能退化成只有一行、只有一列，甚至只有一个数字，因此打印这样的一圈就不再需要四步。图是几个退化的例子，打印一圈分别只需要三步、两步甚至只有一步。

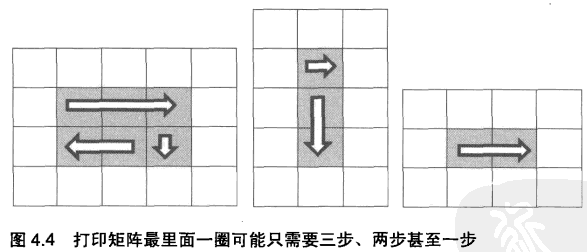
因此我们要仔细分析打印时的每一步的前提条件。第一步总是需要的，因为打印一圈至少需要一步。如果只有一行，那么就不用第二步了。也就是需要第二步的前提条件是终止行号大于起始行号。需要第三步打印的前提条件是圈内至少有两行两列，也就是说除了要求终止行号大于起始行号之外，还要求终止列号大于起始列号。同理，需要打印第四步的前提条件是至少有三行两列，因此要求终止行号比其实行号至少大2，同时终止列号大于起始列号。

代码实现如下：

public class PrintMatrixInCircle {

	public void printMtrix(int[][] matrix){
		int rows = matrix.length;       // 行数
		int columns = matrix[0].length; // 列数
		
		int start = 0;
		// 循环的条件
		while(rows > start * 2 && columns > start * 2){
			printOneCircle(matrix, rows, columns, start);
			start++;
		}
	}

	private void printOneCircle(int[][] matrix, int rows, int columns, int start) {
		
		int xEnd = columns - 1 - start;   // X边界
		int yEnd = rows - 1 - start;      // Y边界
		
		// 从左到右打印一行
		for(int i = start; i <= xEnd; i++){
			int num = matrix[start][i];  // 打印start行
			System.out.print(num +" ");
		}
		
		// 从上到下打印一列
		// 条件：终止行号要大于起始行号
		if(start < yEnd){
			for(int i = start + 1; i <= yEnd; i++){
				int num = matrix[i][xEnd];
				System.out.print(num +" ");
			}
		}
		
		// 从右到左打印一行
		// 条件：终止行号大于起始行号 && 终止列号大于起始列号
		if(start < xEnd && start < yEnd){
			// 从右向左打印，可以画出图看边界条件
			for (int i = xEnd - 1; i >= start; i--) {
				int num = matrix[yEnd][i];
				System.out.print(num +" ");
			}
		}
		
		// 从下到上打印一行
		// 条件：终止行号比起始行号大2 && 终止列号大于起始列号
		if(start < yEnd && start < yEnd - 1){
			for (int i = yEnd - 1; i > start + 1; i--) {
				int num = matrix[i][start];
				System.out.print(num +" ");
			}
		}
	}
	
	public static void main(String[] args) {
		int[][] matrix = {{1,2,3,4},{5,6,7,8},{9,10,11,12}};
		PrintMatrixInCircle pmc = new PrintMatrixInCircle();
		pmc.printMtrix(matrix);  // 1 2 3 4 8 12 11 10 9 6 7 
	}
}

可以发现上诉代码还挺长的，但是其实逻辑还是很清晰的，此类题目最好是在纸上画出图，走一两遍流程，就会发现规律。这道题的重点在于搞清楚每次打印的边界条件。

在牛客网上还看到另外一种方法，不过实际的面试中还是比较推荐上面这种解法，虽然代码较长，但是其实逻辑分析清楚了，还是不难实现的。

public class PrintMatrixInCircle {
	
	/**
	 * 方法二 
	 */
	public ArrayList<Integer> printMatrix(int[][] array){
		ArrayList<Integer> result = new ArrayList<Integer>();
		if(array.length == 0){
			return result;
		}
		int row = array.length;
		int col = array[0].length;
		
		if(col == 0){
			return result;
		}
		
		// 层数：一圈代表一层
		int layer = (Math.min(row, col) - 1) / 2 + 1;   
		
		for(int i = 0; i < layer; i++){
			// 从左到右
			for(int k = i; k < col - i; k++)   result.add(array[i][k]);
			// 从右上到右下
			for(int j = i + 1; j < row - i; j++)  result.add(array[j][col-i-1]);
			// 从右到左
			for(int k = col - i - 2;(k >= i)&&(row - i - 1 != i); k--) result.add(array[row-i-1][k]);
			// 左下到左上
			for(int j = row - i - 2;(j > i)&&(col - i - 1 != i);j--) result.add(array[j][i]);
		}
		return result;
	}
	
	public static void main(String[] args) {
		int[][] matrix = {{1,2,3,4},{5,6,7,8},{9,10,11,12}};
		PrintMatrixInCircle pmc = new PrintMatrixInCircle();
		pmc.printMtrix(matrix);  // 1 2 3 4 8 12 11 10 9 6 7 
	}
}